摘要
我们为零样本分类问题提出了一个原型网络。在这里分类器必须能够被泛化到新类别(在训练集中不可见),每个新类只给出少量示例。
原型网络能够学习一个度量空间,通过计算每个类别的原型表示距离实现分类。与少样本学习近几年的研究方法相比:它们反应了一种更简单的归纳误差,在这种有限数据的情况下是有溢的,并取得了出色的效果,我们提供的分析表明,与最近涉及复杂架构选择和元学习的方法相比。一些简单的设计决策能够产生实质性的改进,进一步将原型网络扩展到零样本学习,并实现最先进得效果在
t
h
e
C
U
−
B
i
r
d
s
d
a
t
a
s
e
the CU-Birds datase
theCU−Birdsdatase数据集上。
介绍
零样本学习是一个任务:分类器能够很好到泛化到训练集中没有的类别。(训练集的每个类都有少量的示例),最近的方法,新数据上的预训练模型能够导致严重的过拟合。这些问题是十分困难的,已经证明显示:人类有能力去执行: o n e − s h o t c l a s s i f i c a t i o n one-shot classification one−shotclassification,(每个新类别仅有一个单独样本给出),加上高度的准确率。
科普
- one-shot classification (从一个类中学习一个二分类器)
介绍(后接上文)
在零样本研究当中,两个近年来的方法已经做出了极大的进步,
-
Vinyals et al :提出了一个匹配网络(matching networks),在支持集的可学习嵌入上使用一个注意力机制,去预测查询集。匹配网络可以解释为将带有权重的最近邻分类器应用在一个嵌入空间中。显著地,模型能够利用样本 m i n i − b a t c h e s mini-batches mini−batches, 在训练集上的多次迭代。
-
设计的每轮迭代都能够最小化零样本任务,通过下采样分类也有数据点。使用迭代能够使得训练问题在测试环境中,更加稳定,能够提高泛化性能。
-
关键点:matching networks、 an attention mechanism、the support set、the query set、a weighted nearest-neighbor classifier、sampled mini-batches、subsampling classes、
data points、 -
Ravi and Larochelle
利用迭代训练思想进一步和提出了少样本学习的元学习的方法。
这些方法涉及到训练一个LSTM,去产生更新的分类器,给一个迭代,因此,其将会在测试集上取得更好的泛化性能。
而不是在单一个模型上多次迭代,LSTM元学习器为每次迭代学习一个训练一个自定义模型。
通过解决过拟合来处理零样本学习的问题,因此,数据是非常有限的,我们工作的假定是分类器有一个简单的归纳偏差,我们的方法,原型网络是基于这种思想,每个类别单一的原型表示points cluster存在一个嵌入。
为了解决这些,我们使用神经网络学习一个非线性映射将输入映射进嵌入空间。利用一个类原型:嵌入空间中支持集的平均值。查询点找到最近类原型来进行分类。
我们按照相同的方法去处理零样本学习,因此,每个类别都使用更高级别描述的元数据,而不是一个简单的标签示例,因此,将元学习嵌入到共享空间为了服务每个类的原型。
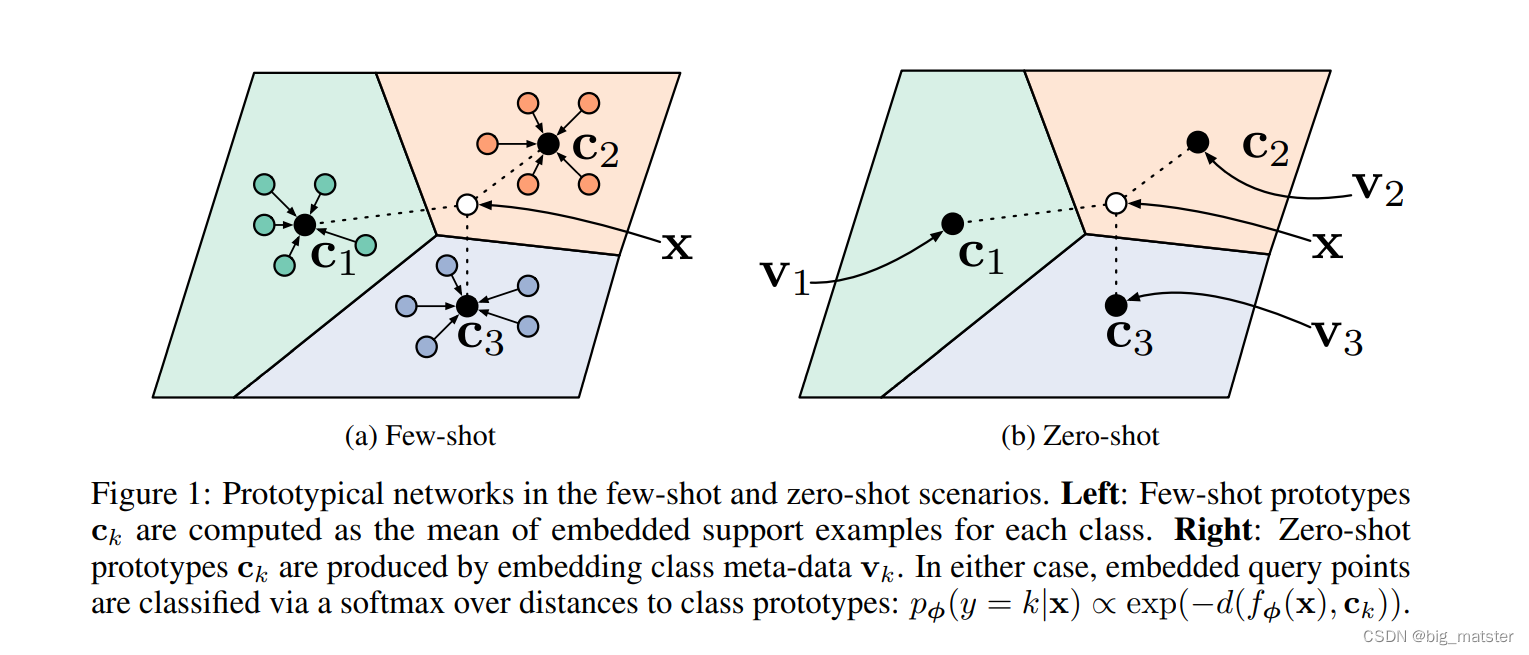
在零样本场景中,分类可以被执行**,通过依据嵌入查询点发现最近类原型**。
在这篇论文中,我们计算类原型网络通过零样本和少样本集合。在单个样本集中我们阐述匹配网络
(matching networks)和(the one-shot setting)
在模型中,使用
t
h
e
u
n
d
e
r
l
y
i
n
g
d
i
s
t
a
n
c
e
f
u
n
c
t
i
o
n
the underlying distance function
theunderlyingdistancefunction,
特别地,我们将原型网络相关到聚类,为了验证使用类均值作为原型的正当性。Bregman 散度来计算距离原型,
比如:欧氏距离。
富有经验的发现,距离的选取是至关重要的,因为欧氏距离可以极大优于余弦函数距离(
c
o
s
i
n
e
,
s
i
m
i
l
a
r
i
t
y
cosine,similarity
cosine,similarity)
在一些基准任务上,我们实现了一些顶级的效果。原型网络比近年来的元学习算法更假简单和更加有效,使其称为零样本和少样本学习方法更加的受欢迎。
原型网络
Notation
在零样本分类中,我们
*我们给予一个
N
l
a
b
e
l
e
d
e
x
a
m
p
l
e
s
N labeled examples
Nlabeledexamples的支持集。
{
(
x
1
,
y
1
)
,
.
.
.
,
(
x
N
,
y
N
)
{(x_1, y_1), . . . ,(x_N , y_N )}
(x1,y1),...,(xN,yN)}
x
i
∈
R
D
x_i \in R^D
xi∈RD 是例子中的D维特征向量$ the D-dimensional feature vector$
y
i
y_i
yi
∈
\in
∈ {
1
,
⋯
,
K
1,\cdots,K
1,⋯,K} 与特征向量相同维度的标签空间。
S
k
S_k
Sk 表示有标签集合中的
c
l
a
s
s
,
k
class,k
class,k
模型
原型网络计算一个
a
n
M
−
d
i
m
e
n
s
i
o
n
a
l
r
e
p
r
e
s
e
n
t
a
t
i
o
n
an M-dimensional representation
anM−dimensionalrepresentation
原型:
c
k
∈
R
M
c_k \in R^{M}
ck∈RM
- 每个类通过一个嵌入函数:
f ϕ : R D → R M f_{\phi}:R^{D}\rightarrow R^{M} fϕ:RD→RM 加上学习参数 ϕ \phi ϕ - 每个类的原型都是嵌入支持点的均值向量,该支持点归属于其类别。
- 类原型
c K = 1 ∣ S K ∣ ∑ ( x i , y i ) ∈ S k f ϕ ( x i ) c_K = \frac{1}{|S_K|}\sum_{(x_i,y_i) \in S_k}f_{\phi}(x_i) cK=∣SK∣1(xi,yi)∈Sk∑fϕ(xi) - 给出一个距离函数
d
:
R
M
×
R
M
d:R^{M} \times R^{M}
d:RM×RM
→
[
0
,
∞
)
\rightarrow [0,\infty)
→[0,∞)
原型网络为查询点 x x x产生一个分布类,在嵌入空间中,基于 S o f t m a x Softmax Softmax函数的原型,在嵌入空间中。
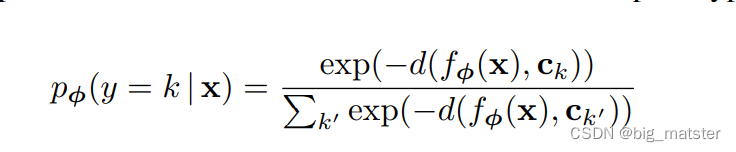
通过最小化负对数似然概率来进行学习过程:
J
(
ϕ
)
=
−
l
o
g
p
ϕ
(
y
=
k
∣
x
)
J(\phi) = -logp_{\phi}(y = k|x)
J(ϕ)=−logpϕ(y=k∣x)
真实类别
k
l
kl
kl,验证
S
G
D
SGD
SGD.
通过随机的从训练集中选择一系列类,完成迭代过程。
选择一系列支持集的示例.和一系列查询点示例。
- query points
- the support points
使用以下算法1,来最小化 J ( ϕ ) J(\phi) J(ϕ)
算法思想:随机采样+最小化损失函数

原型网络作为混合密度估计
距离函数的特定类,被定义为:
r
e
g
u
l
a
r
B
r
e
g
m
a
n
d
i
v
e
r
g
e
n
c
e
s
regular Bregman divergences
regularBregmandivergences,
原型网络算法可以实现相等的效果与支持集上的混合密度估计加一个指数分布簇。
$ mixture density estimation on the support set $,
a
n
,
e
x
p
o
n
e
n
t
i
a
l
,
f
a
m
i
l
y
,
d
e
n
s
i
t
y
an, exponential,family,density
an,exponential,family,density
正则的Bregman度量可以定义为:
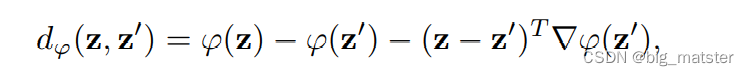
ϕ
\phi
ϕ是严格的凸二次可微函数。
B
r
e
g
m
a
n
Bregman
Bregman度量的例子包括:均方欧氏距离和马哈顿距离。
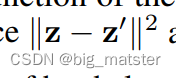
原型计算能够被观看到在支持集上的硬聚类。
Prototype computation can be viewed in terms of hard clustering on the support set, with one cluster per class and each support point assigned to its corresponding class cluster. It has been shown [4] for Bregman divergences that the cluster representative achieving minimal distance to its assigned points is the cluster mean. Thus the prototype computation in Equation (1) yields optimal cluster representatives given the support set labels when a Bregman divergence is used.


可解释线性模型

与匹配网络相比较
Matchine networks:
- a weighted nearest neighbor classifier given the support set
prototypical networks
-
produce a linear classifier when squared Euclidean distance is used
-
ordinary gradient descent methods
决策选择
- Distance metric
- squared Euclidean distance
- Episode composition

零样本学习
c
k
=
g
ϑ
(
v
k
)
c_k = g_ϑ(v_k)
ck=gϑ(vk)
原数据向量和查询点来自不同的输入域。
(the meta-data vector and querypoint)
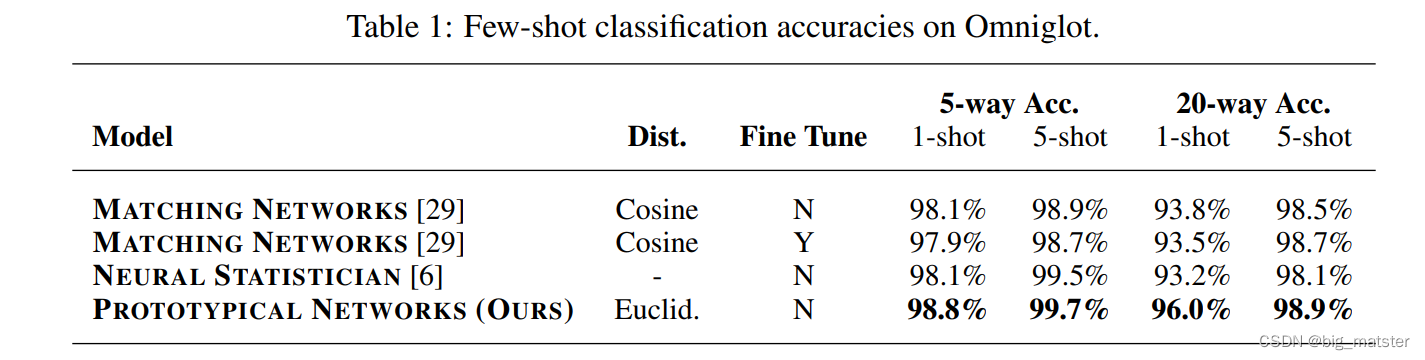
实验
- 训练方式:a,SGD,with Adam
miniImageNet Few-shot Classification
- ILSVRC-12 dataset
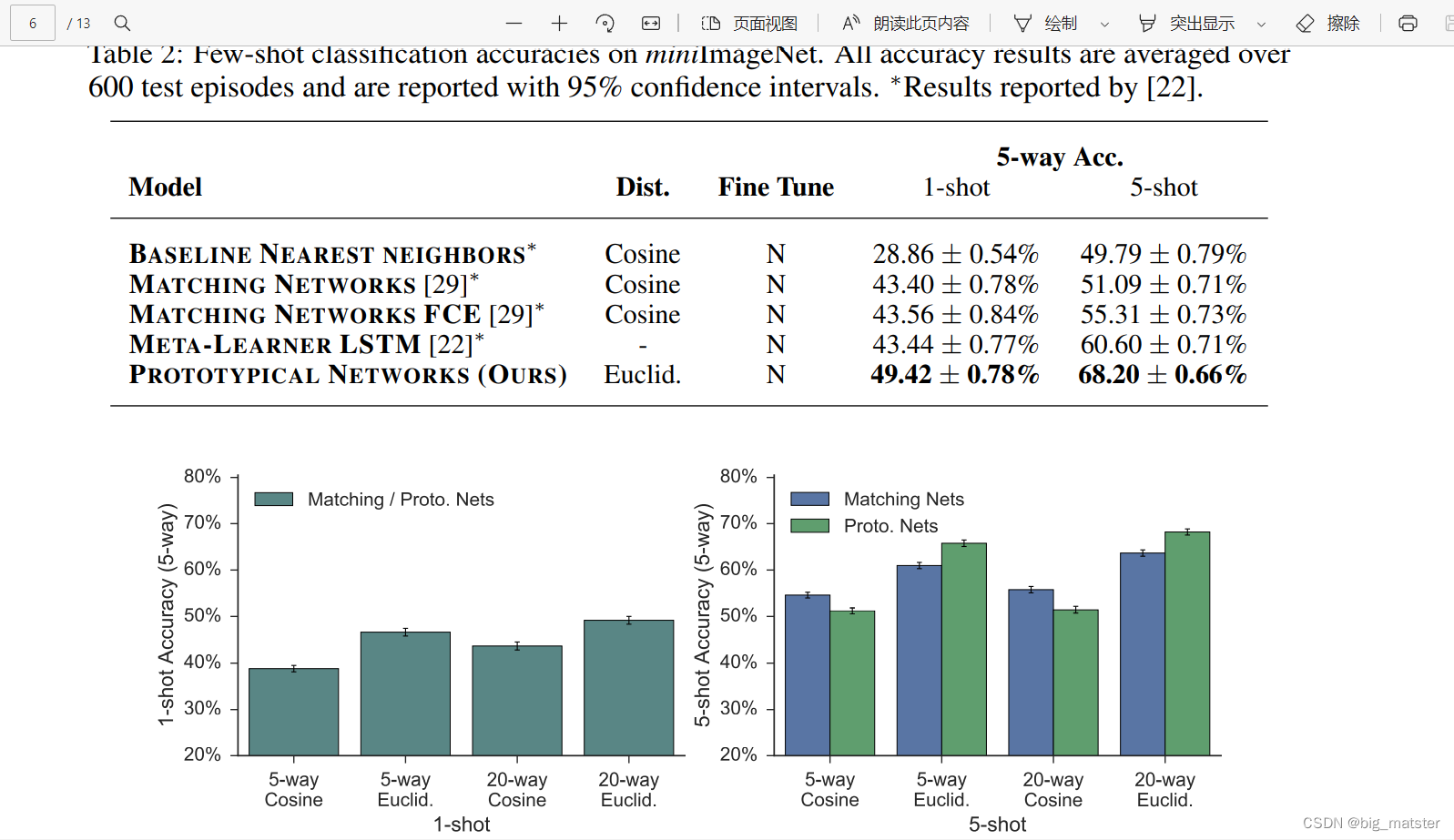
基准模型
- two non-fine-tuned variants of matching networks
- the Meta-Learner LSTM 和 FCE
CUB Zero-shot Classification
- the Caltech-UCSD Birds (CUB) 200-2011 dataset
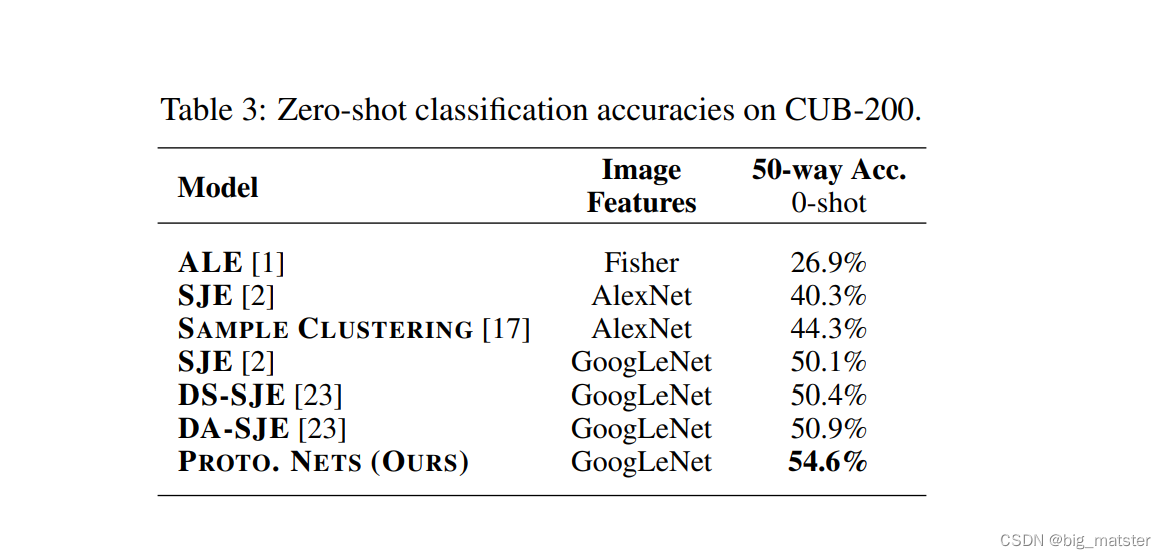
- Early stopping (早停法)
相关工作

- the variational autoencoder [(变体自编码)
结论
- the simplicity and effectiveness of prototypical networks makes it a promising approach for few-shot learning
概览
原型网络大致搞明白啦,明天学会将其运用在代码框架上,并将其研究一番。
全部都将其搞定都行啦的回事与打算。会将这个原型网络用于代码学习与研究上。
会自己仔细斟酌透彻,仔细研究一番。全部都将其搞定都行啦的回事与打算。
明天自己把代码跑一波
一个广义零样本的基本模型方法就搞懂啦。
总结
大致理解以下,然后自己慢慢的开始搞代码,都行啦的样子与打算。
大致了解一波,公式推断原理,然后慢慢的开始搞起来都行啦的回事与打算。
- 数据集的概览,先进行观察数据集,运行代码的时候,在自己运行各种数据集及其他的样子与打算。
- 重点学得深入后会自己推导公式。


![[附源码]计算机毕业设计JAVA疫苗接种管理系统](https://img-blog.csdnimg.cn/baf9ef2f7a804060ab4f6b887163a792.png)



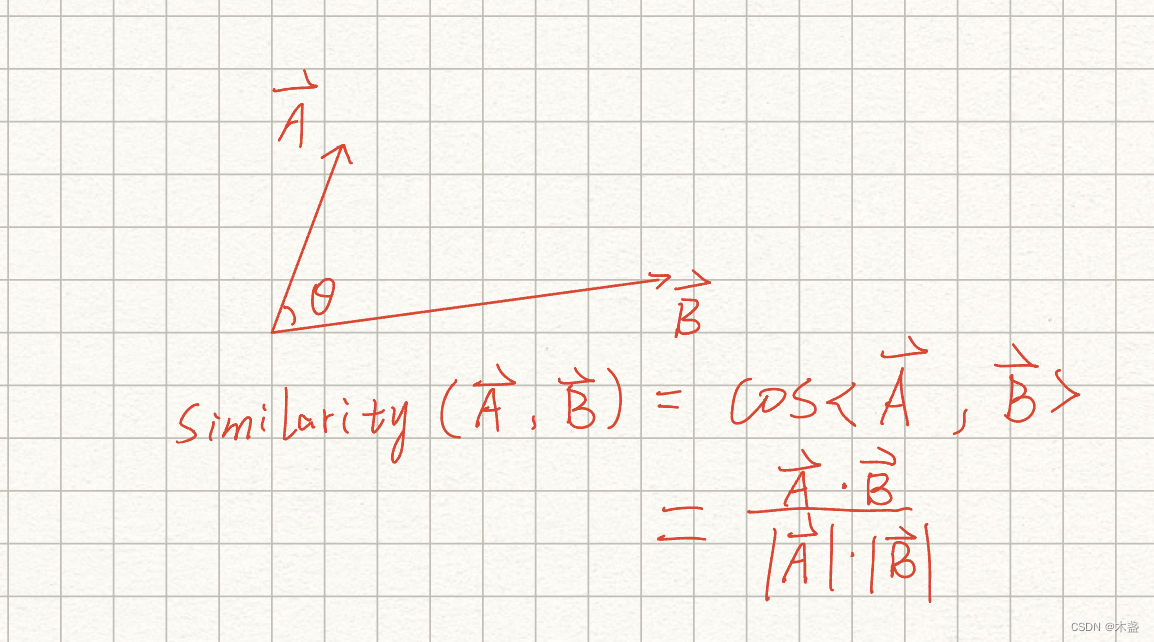

![[附源码]计算机毕业设计基于Springboot甜品购物网站](https://img-blog.csdnimg.cn/5f71617ab0fc41a7bd9f8b19df3353f2.png)