文章目录
- 题目
- 34. 在排序数组中查找元素的第一个和最后一个位置
- 240. 搜索二维矩阵
- 378. 有序矩阵中第 K 小的元素
- 287. 寻找重复数
- 33. 搜索旋转排序数组
- 总结
题目
34. 在排序数组中查找元素的第一个和最后一个位置

原始思路:
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
# 1. 一般情况:利用二分查找不断缩小区间,直到找到target所在的位置,然后通过左右移动确定最终target所在的区间。
# 2. 考虑list为空的情况。
# 3. 考虑low high本身就等于target的情况。
n = len(nums)
if n == 0:
return [-1, -1]
low = 0
high = n - 1
while(high - low > 1):
mid = (low + high) // 2
if nums[mid] > target:
high = mid - 1
else:
low = mid
if nums[high] == target:
low = high
if n == 0 or nums[low] != target:
return [-1, -1]
else:
# 以最终的mid为起点,往两边挪一挪
while(low - 1 >= 0 and nums[low - 1] == nums[low]):
low -= 1
high = low
while(high + 1 <= n-1 and nums[high + 1] == nums[low]):
high += 1
return [low, high]
但是,挪一挪的步骤最差的时候时间复杂度也能达到O(n),所以另一种避免这种情况的思路是我们分别使用二分查找去寻找区间的最左和最右。
上面的寻找target的代码(while …)无法精确地找到最左,因此我们需要对其进行一些改写。关键是要在找到一个值的时候不跳出循环,而是继续往左或者往右二分查找当前值。
class Solution:
def searchRange(self, nums: List[int], target: int) -> List[int]:
n = len(nums)
low, high = 0, n - 1
left, right = 0, 0
# 寻找最左
while(low <= high):
mid = (low + high) // 2
if nums[mid] > target:
high = mid - 1
elif nums[mid] < target:
low = mid + 1
else:
left = mid
high = mid - 1 # 加上等于target的条件,可以在找到的时候继续往左边找
# 没找到的情况
if len(nums) == 0 or nums[left] != target:
return [-1, -1]
high = n - 1
# 寻找最右
while(low <= high):
mid = (low + high) // 2
print(mid, nums[mid], target)
if nums[mid] > target:
high = mid - 1
elif nums[mid] < target:
low = mid + 1
else:
right = mid
low = mid + 1 # 加上等于target的条件,可以在找到的时候继续往左边找
return [left, right]
240. 搜索二维矩阵
这个矩阵可以视为左上角为root的二叉搜索树。(也可以右下角为root,改一下变大变小的规则就行)

class Solution:
def searchMatrix(self, matrix: List[List[int]], target: int) -> bool:
# 初始位置:(i, j)
# 如果target比cur_val (i,j)大,则变成(i+1, j)
# 如果target比cur_val (i,j)小,则变成(i, j-1)
m = len(matrix)
n = len(matrix[0])
i = 0
j = n - 1
while(i < m and j >= 0):
cur_val = matrix[i][j]
print(i, j, cur_val, target)
if cur_val == target:
return True
elif cur_val > target:
j -= 1
else:
i += 1
return False
378. 有序矩阵中第 K 小的元素
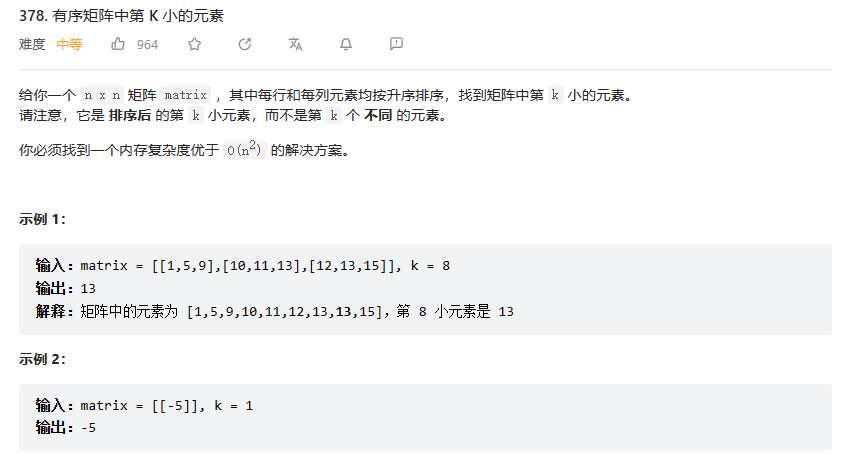
与上一题类似,利用矩阵两个方向递增的性质。
class Solution:
def kthSmallest(self, matrix: List[List[int]], k: int) -> int:
# 1 5 9
# 10 [11] 13
# *12 13 13
# 同样的,把这个矩阵视作一个二叉搜索树
# 判断矩阵中小于等于mid的值是否有k个
# 如果有的话,就往左半部分继续找
# 如果没有,就往右半部分继续找
def cal(matrix, mid, n):
# O(n) 计算小于等于mid的值的个数
i = n - 1
j = 0
num = 0
while(i >= 0 and j < n):
if matrix[i][j] <= mid:
num += i + 1 # 这种情况所在的一列都可以不看了
j += 1 # 往右边大的方向走
else:
i -= 1 # 往上面往小的方向走
return num
n = len(matrix)
left = matrix[0][0]
right = matrix[n-1][n-1]
while(left < right):
mid = left + (right - left) // 2
left_num = cal(matrix, mid, n)
# 这种写法是错误的,因为有可能mid不在矩阵中
# if left_num > k:
# right = mid - 1
# elif left_num == k:
# return mid
# else:
# left = mid + 1
if left_num >= k:
# 可能等于mid也可能不等于
right = mid
else:
# 肯定需要继续往右找
left = mid + 1
# 返回left或者right都是一样的
return left
287. 寻找重复数
只有一个数字会重复,但是一个数字可能会重复多次。
class Solution:
def findDuplicate(self, nums: List[int]) -> int:
n = len(nums)
# 如果不考虑空间复杂度 O(n)的时间复杂度
# times_dict = {}
# for n in nums:
# if n not in times_dict.keys():
# times_dict[n] = 1
# else:
# return n
# 运用二分法实现O(1)复杂度的方法
# 对于数字i,如果小于i的数字没有i-1个,则说明其重复了
low = 1
high = n
while(low < high):
mid = low + (high - low) // 2
counter = 0
for n in nums:
if n <= mid:
counter += 1
if counter > mid:
# 继续往mid左边找,包括mid
# 像这种low或者high可能等于mid的,就用while(low < high)否则可能跳不出循环
high = mid
elif counter <= mid:
# 正常,往右边找,不包括mid
low = mid + 1
# 返回low和high都是一样的
return low
33. 搜索旋转排序数组
这一题主要需要理解当你设置一个中间值的时候,左半部分或者右半部分总有一个是有序的。确认了哪部分是有序的之后,我们就更方便确定区间是在左边还是在右边了。
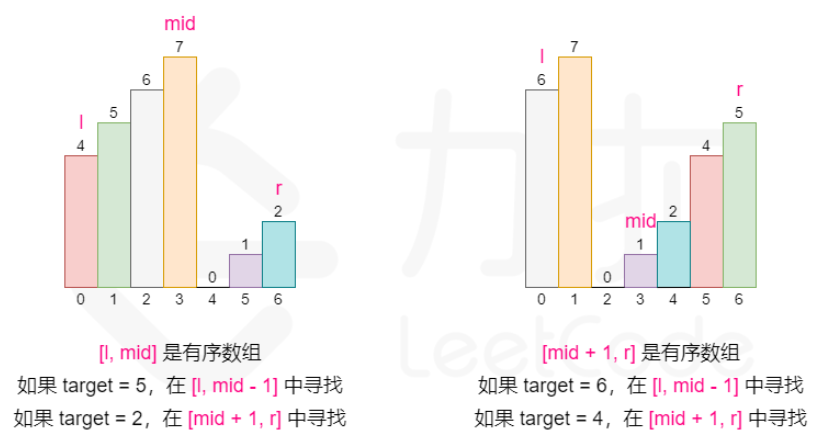
class Solution:
def search(self, nums: List[int], target: int) -> int:
n = len(nums)
low = 0
high = n - 1
# 旋转后的数组是局部有序的,且无论如何,左右总会有一半是有序的
while(low <= high): # 加上等于号防止与return -1的情况混淆
mid = low + (high - low) // 2
if nums[mid] == target:
return mid
# 如果左边是有序的,那肯定是从小到大
if nums[0] <= nums[mid]:
if nums[low] <= target < nums[mid]:
high = mid - 1
else:
low = mid + 1
# 如果右边是有序的,肯定也是从小到大
else:
if nums[mid] < target <= nums[high]:
low = mid + 1
else:
high = mid - 1
return -1
总结
- 二分查找适合有序或部分有序的数组或者矩阵。
- 需要注意的点:
a. 二分查找结束点的确定:如果中间high或者low可能等于mid,那么就用low < high作为循环结束条件;否则用low <= high作为循环结束条件,因为反正不会相等。
b. 二分查找左右区间的赋值:看需求,主要需要判断以下什么情况更新low/high为mid / mid+1 / mid-1。
c. 二分查找最后返回值的确定:因为最后跳出来的时候一般high=low,所以返回最终的high或者low即可。