目录

一. 关于快速排序思路的产生

二. 快速排序的实现

        1. 快速排序的实现

        2. 快速排序的效率分析

三. 快速排序的代码实现

        1. 快速排序

        2. 快速排序核心代码：

四. 代码展示

五. 数据测试

六. 总结

---

一. 关于快速排序思路的产生

        从现在开始，让我们假设需要被排好序的事物列表是一些需要按升序排列的数字（算法对任何其它对象列表和顺序都是一样的。）给定这样一个数字列表，怎么样尽可能快速的将这一串数字序列排列好呢?

        我们之前学习的算法——类似于冒泡，直接插入，希尔排序都是基于序列本身的，我们现在能否找一个利用分而治之和递归的思想来进行排序的算法呢？意思就是我能不能将序列分成几段，在这分好的小段中又分段，这样迭代进行下去，直到只剩下一个数字，最后再把这拍好的数字组合起来，那不就对序列排好序了吗？

        于是乎快速排序——被誉为是最好的排序算法之一诞生了。

 

二. 快速排序的实现

        1. 快速排序的实现

        快速排序的基本思想是基于分治法的，在待排序表L[1...n]中任取一个元素pivot作为枢轴（或称基准），通过一趟排序将待排序表划分为独立的两个部分L[1...k-1]和L[k+1...n]，使得L[1...k-1]中的所有元素小于pivot，L[k+1...n]中的所有元素大于或等于pivot，则pivot放在了其最终位置L（k）上，这个过程称为一次划分。然后分别递归的对两个子表重复上述过程，直到每部分内只有一个元素或为空为止，即所有元素放在了其最终位置上。

        一趟快速排序的过程是一个交替搜索和交换的过程，下面通过实例介绍：

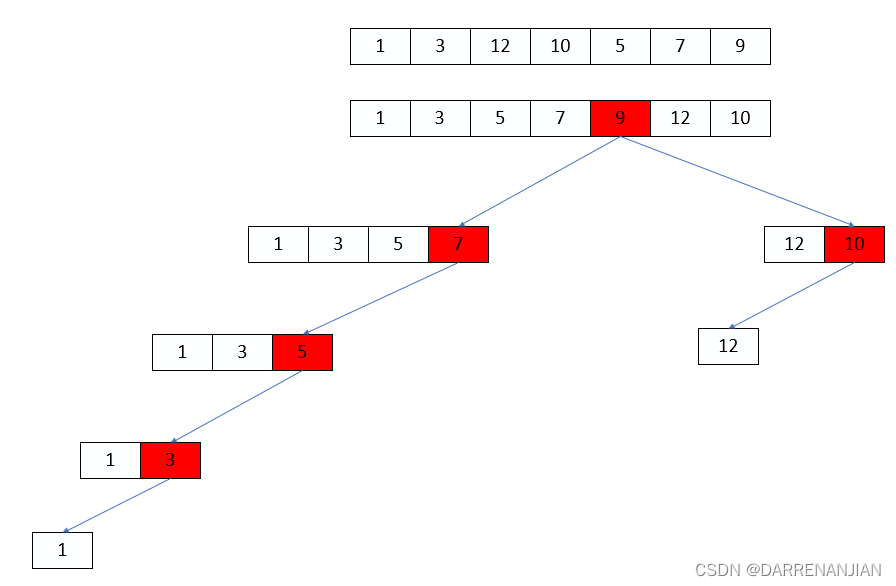
         可以发现每一轮我们选定一个量作为分段的依据，接着分好的子段进行同样的操作，直到得到最终的结果。

        2. 快速排序的效率分析

        空间效率：由于快速排序是递归的，需要借助一个递归调用栈来保存每层递归调用的必要信息，其容量与调用的最大深度一致。最好情况下为；最坏情况下，因为要进行n-1次递归调用，所以栈的深度为；平均情况下，栈的深度为。

         时间效率：快速排序的运行时间与划分是否对称有关，快速排序的最坏情况发生在两个区域分别为n-1个元素和0个元素时，这种最大限度的不对称性若发生在每层递归上，即对应于初始排序表基本有序或者基本逆序时，就得到最坏情况下的时间复杂度为；在最理想情况下，即枢轴量每次都做到最平衡的划分，得到的两个子问题的大小都不可能大于n/2，在这种情况下，快速排序的运行速度将大大提升，此时，时间复杂度为。好的快速排序平均情况下的运行时间与其最佳情况下的运行时间很接近而不是接近其最坏情况下的运行时间。快速排序是所有内部排序算法中平均性能最优的排序算法。

        稳定性：在划分算法中，若右端区间有两个关键字相同，且均小于基准值的记录，则在交换到左端区间后，它们的相对位置发生了变化，即快速排序是一种不稳定的排序方法。

         可以发现，每次枢轴量刚好取到能几乎平分字段时，效率最快，并且深度最低；若每次取到的枢轴量为最大（最小）值时，效率最低，并且深度最大。

三. 快速排序的代码实现

        1. 快速排序

        这部分代码不是核心，相当于确定一个排序的开头start和排序的结尾end。

    /**
     *********************
     * Quick sort.
     *********************
     */
    public void quickSort() {
        quickSortRecursive(0, length - 1);
    }// Of quickSort

        2. 快速排序核心代码：

        首先确定边界是否合法，若Start >= End直接结束调用。

        找到第一个枢轴量存在的位置，然后将两者互换位置，接着调入下一轮递归。（我觉得这些东西都很简单，按着代码来理解就好了，关键是理解背后的思想，接着用代码实现就可以了，代码的过程可能和人想的过程不一样，但是实现得到的最终结果是一样的）。

    /**
     *********************
     * Quick sort recursively.
     *
     * @param paraStart The start index.
     * @param paraEnd   The end index.
     *********************
     */
    public void quickSortRecursive(int paraStart, int paraEnd) {
        // Nothing to sort.
        if (paraStart >= paraEnd) {
            return;
        } // Of if

        int tempPivot = data[paraEnd].key;
        DataNode tempNodeForSwap;

        int tempLeft = paraStart;
        int tempRight = paraEnd - 1;

        // Find the position for the pivot.
        // At the same time move smaller elements to the left and bigger one to the
        // right.
        while (true) {
            while ((data[tempLeft].key < tempPivot) && (tempLeft < tempRight)) {
                tempLeft++;
            } // Of while

            while ((data[tempRight].key >= tempPivot) && (tempLeft < tempRight)) {
                tempRight--;
            } // Of while

            if (tempLeft < tempRight) {
                // Swap.
                System.out.println("Swapping " + tempLeft + " and " + tempRight);
                tempNodeForSwap = data[tempLeft];
                data[tempLeft] = data[tempRight];
                data[tempRight] = tempNodeForSwap;
            } else {
                break;
            } // Of if
        } // Of while

        // Swap
        if (data[tempLeft].key > tempPivot) {
            tempNodeForSwap = data[paraEnd];
            data[paraEnd] = data[tempLeft];
            data[tempLeft] = tempNodeForSwap;
        } else {
            tempLeft++;
        } // Of if

        System.out.print("From " + paraStart + " to " + paraEnd + ": ");
        System.out.println(this);

        quickSortRecursive(paraStart, tempLeft - 1);
        quickSortRecursive(tempLeft + 1, paraEnd);
    }// Of quickSortRecursive

四. 代码展示

        主类：

package Day_46;

import Day_41.DataArray;

public class demo1 {
    /**
     *********************
     * The entrance of the program.
     *
     * @param args Not used now.
     *********************
     */
    public static void main(String args[]) {
//        System.out.println("\r\n-------sequentialSearchTest-------");
        int []paraKeyArray;
        paraKeyArray=new int[]{11,2,3};
        String[] paraContentArray = new String[]{"121","21","324"};
        DataArray test=new DataArray(paraKeyArray,paraContentArray);

//        test.insertionSort();
//        System.out.println("Result\r\n" + test);
        test.quickSortTest();


    }// Of main
}

        调用类：

    /**
     *********************
     * Quick sort recursively.
     *
     * @param paraStart The start index.
     * @param paraEnd   The end index.
     *********************
     */
    public void quickSortRecursive(int paraStart, int paraEnd) {
        // Nothing to sort.
        if (paraStart >= paraEnd) {
            return;
        } // Of if

        int tempPivot = data[paraEnd].key;
        DataNode tempNodeForSwap;

        int tempLeft = paraStart;
        int tempRight = paraEnd - 1;

        // Find the position for the pivot.
        // At the same time move smaller elements to the left and bigger one to the
        // right.
        while (true) {
            while ((data[tempLeft].key < tempPivot) && (tempLeft < tempRight)) {
                tempLeft++;
            } // Of while

            while ((data[tempRight].key >= tempPivot) && (tempLeft < tempRight)) {
                tempRight--;
            } // Of while

            if (tempLeft < tempRight) {
                // Swap.
                System.out.println("Swapping " + tempLeft + " and " + tempRight);
                tempNodeForSwap = data[tempLeft];
                data[tempLeft] = data[tempRight];
                data[tempRight] = tempNodeForSwap;
            } else {
                break;
            } // Of if
        } // Of while

        // Swap
        if (data[tempLeft].key > tempPivot) {
            tempNodeForSwap = data[paraEnd];
            data[paraEnd] = data[tempLeft];
            data[tempLeft] = tempNodeForSwap;
        } else {
            tempLeft++;
        } // Of if

        System.out.print("From " + paraStart + " to " + paraEnd + ": ");
        System.out.println(this);

        quickSortRecursive(paraStart, tempLeft - 1);
        quickSortRecursive(tempLeft + 1, paraEnd);
    }// Of quickSortRecursive

    /**
     *********************
     * Quick sort.
     *********************
     */
    public void quickSort() {
        quickSortRecursive(0, length - 1);
    }// Of quickSort

    /**
     *********************
     * Test the method.
     *********************
     */
    public static void quickSortTest() {
        int[] tempUnsortedKeys = { 1, 3, 12, 10, 5, 7, 9 };
        String[] tempContents = { "if", "then", "else", "switch", "case", "for", "while" };
        DataArray tempDataArray = new DataArray(tempUnsortedKeys, tempContents);

        System.out.println(tempDataArray);

        tempDataArray.quickSort();
        System.out.println("Result\r\n" + tempDataArray);
    }// Of quickSortTest

五. 数据测试

        运行得到的结果如图所示：

六. 总结

        这一部分的排序代码可能确实要比插入和冒泡难一点，但是我觉得可以接受，其实本质思想就一个——分而治之，根据从数组里面找到的枢轴量，把数组分成两个部分，再对这两个部分重复上述的操作，最后得到排序结果即可。不过这里我们可以发现有重复调用的情况出现，所以这里一定会有栈（递归）等方式的出现，一旦有这个递归出现就意味着需要额外空间来存储数据，所以这个快速排序算法并不是原地算法，需要额外的空间。这个所需空间的大小和排序调用层数有关（时间复杂度也和这个相关，具体的详见上文。）