为什么要进行微调？

在快速发展的人工智能领域中，以高效和有效的方式使用大型语言模型变得越来越重要。
预训练的大型语言模型通常被称为优秀的基础模型，原因在于它们在各种任务上表现出色，

而大模型微调是将其适应到特定的目标任务或领域中。尽管预训练的大型语言模型在各种任务上表现出色，但它们并不是为特定任务而设计的。通过微调，我们可以根据目标任务的需求对模型进行调整，使其在该任务上的性能得到进一步提升。
微调使我们能够将模型调整到目标领域和目标任务。然而，它在计算上可能非常昂贵-模型越大，更新其层的成本就越高。作为更新所有层的替代方法，已经开发了参数高效的方法，例如前缀调整和适配器。

现在，又出现了一种更流行的参数高效微调技术：
低秩适应（LoRA）。LoRA是什么？它是如何工作的？与其他流行的微调方法相比如何？让我们在本文中回答所有这些问题！

LoRA思路

低秩适应（Low-Rank Adaptation）是一种参数高效的微调技术，其核心思想是对大型模型的权重矩阵进行隐式的低秩转换。

什么是低秩转换呢？

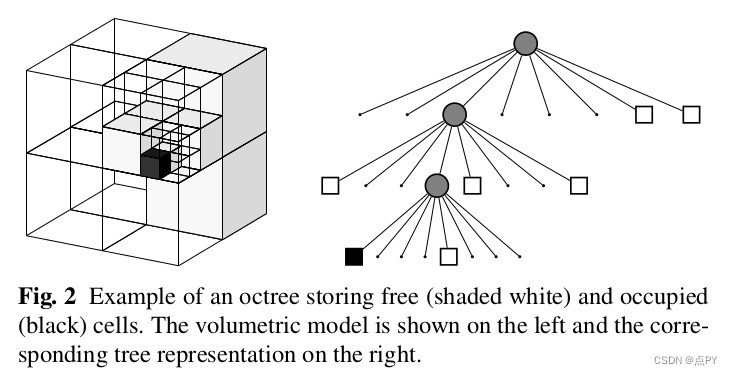
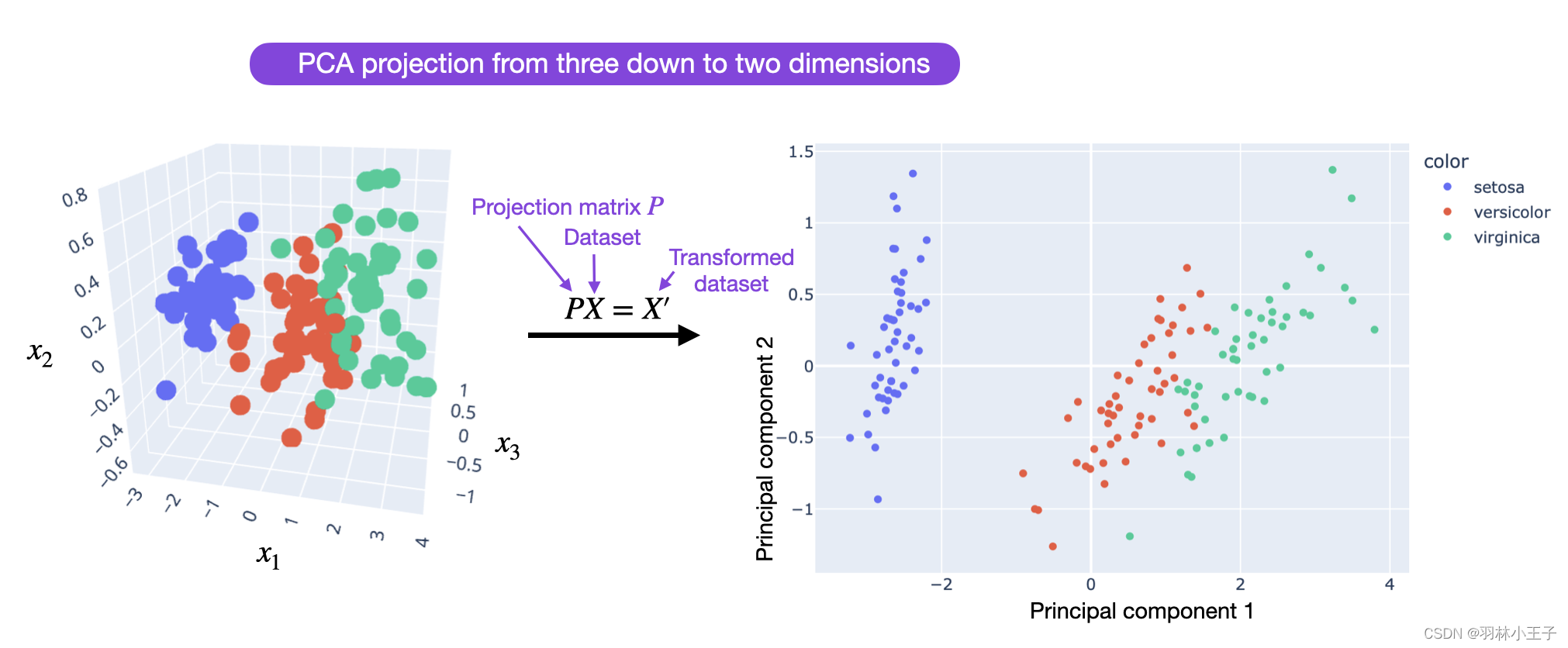
整体的想法和概念与主成分分析（PCA）和奇异值分解（SVD）有关，我们通过一个较低维度的表示来近似表示一个高维矩阵或数据集。

换句话说，我们试图找到原始特征空间（或矩阵）中少数维度的（线性）组合，能够捕捉数据集中大部分的信息。
如下图所示：
在这里插入图片描述

提高权重更新效率

LoRA: Low-Rank Adaptation of Large Language Models 这篇论文提出了将权重变化 $Δ W$ 分解为一个低秩表示的方法。（严格来说，LoRA 并不直接对矩阵进行分解，而是通过反向传播学习分解后的矩阵）。

在我们深入了解 LoRA 之前，先简要解释一下正常微调期间的训练过程。权重 $Δ W$ 是如何变换的

假设 $W$ 表示神经网络层中的权重矩阵。
使用常规的反向传播，我们可以得到权重更新 $Δ W$ ，
通常计算为损失的负梯度乘以学习率：
$\Delta W = \alpha ( -\nabla L_W)$ 。

然后，当我们有了 $Δ W$ 之后，我们可以按照以下方式更新原始权重：
$W^{'} = W + Δ W$ 。

下图中展示了这个过程，为了方便理解LoRA的思想，我们将权重更新矩阵 $\Delta W$ 和原始 $W$ 保持分开展示，并按照以下方式计算输出：
$\Delta W)x$
$\Delta W x$ ，
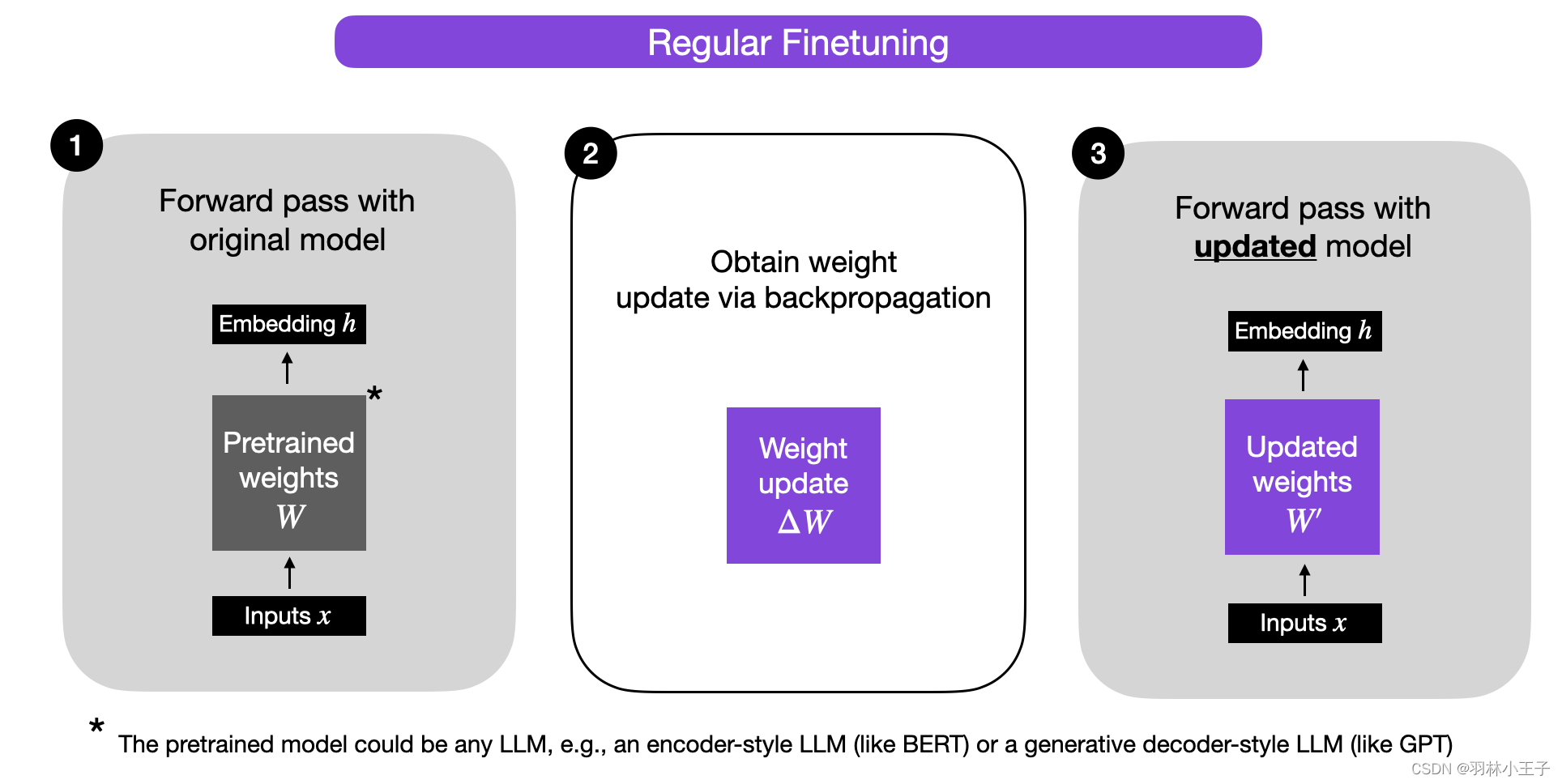
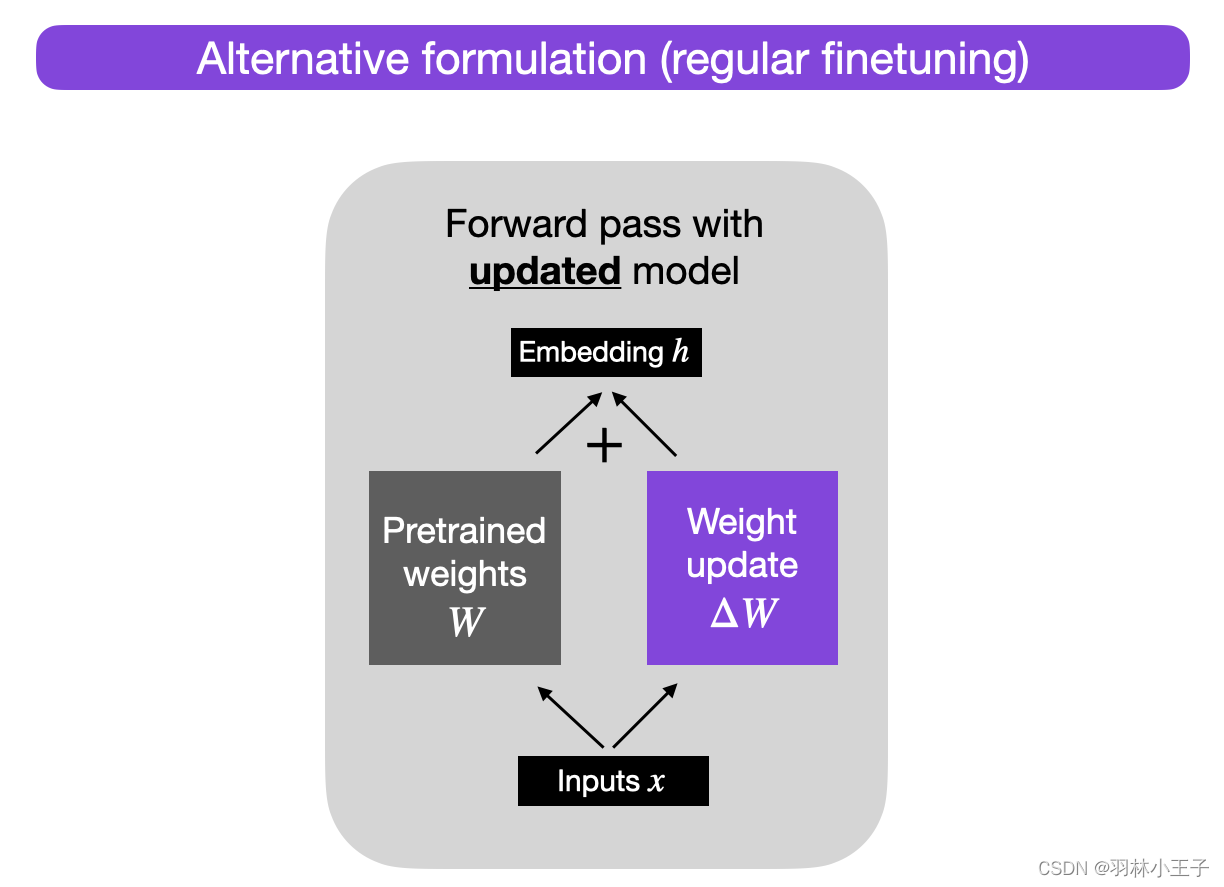
在这里插入图片描述

当我们训练神经网络中的全连接（即“稠密”）层时，如上图所示，权重矩阵通常具有完整秩（full rank）。完整秩是一个技术术语，意味着矩阵的行或列之间没有线性相关（即“冗余”）关系。相反，与完整秩相对应，低秩意味着矩阵具有冗余的行或列。详细理解如下图所示：

在深度学习中，权重矩阵通常具有完整秩，这意味着权重矩阵的行或列之间没有线性相关关系，也就是说，每个权重在模型中承担了不同的作用，没有冗余。这种情况下，权重矩阵能够充分表达模型的复杂性和丰富的特征表示能力。权重矩阵具有完整秩的好处是，模型可以通过学习到的权重进行准确的预测和分类。每个权重都对模型的输出产生影响，而且没有多余的冗余信息。
然而，在某些情况下，完整秩的权重矩阵可能会导致一些问题。例如，当训练数据量较少或数据噪声较多时，权重矩阵可能会过拟合，导致模型泛化能力下降。此外，权重矩阵中的大量参数可能会导致计算和存储的开销很大。
因此，在一些参数效率方面的研究中，人们开始关注如何利用低秩矩阵来表示权重矩阵。通过使用低秩矩阵，我们可以降低参数的数量，减少计算和存储的开销，并且仍然保留了大部分原始权重矩阵的关键信息。这样，我们可以在保持模型性能的同时，提高计算效率和模型的可解释性

因此，虽然预训练模型的权重在预训练任务中具有完整秩，但LoRA的作者指出，当预训练的大型语言模型适应新任务时，其固有维度很低，这是根据Aghajanyan等人的研究（2020）得出的。（换句话说：实际微调后的权重其实对比原始模型，能用到的权重其实很少）

低秩维度意味着数据可以通过较低维度的空间有效表示或近似，同时保留其大部分重要信息或结构。换句话说，这意味着我们可以将适应任务的新权重矩阵分解为较低维度（较小）的矩阵，而不会丢失太多重要信息。

例如，假设 $Δ W$ 是权重矩阵 $\in \mathbb{R}^{A \times B}$ 的权重更新。然后，我们可以将权重更新矩阵分解为两个较小的矩阵： $ΔW=W_AW_B$ ，其中 $W_A\mathbb{R}^{A \times r}$ 且 $W_B\mathbb{R}^{r \times B}$ 。
在这里，我们保持原始权重 $W$ 不变，只训练新的矩阵 $W_A$ 和 $W_B$ 。简言之，这就是LoRA方法的核心思想，如下图所示。
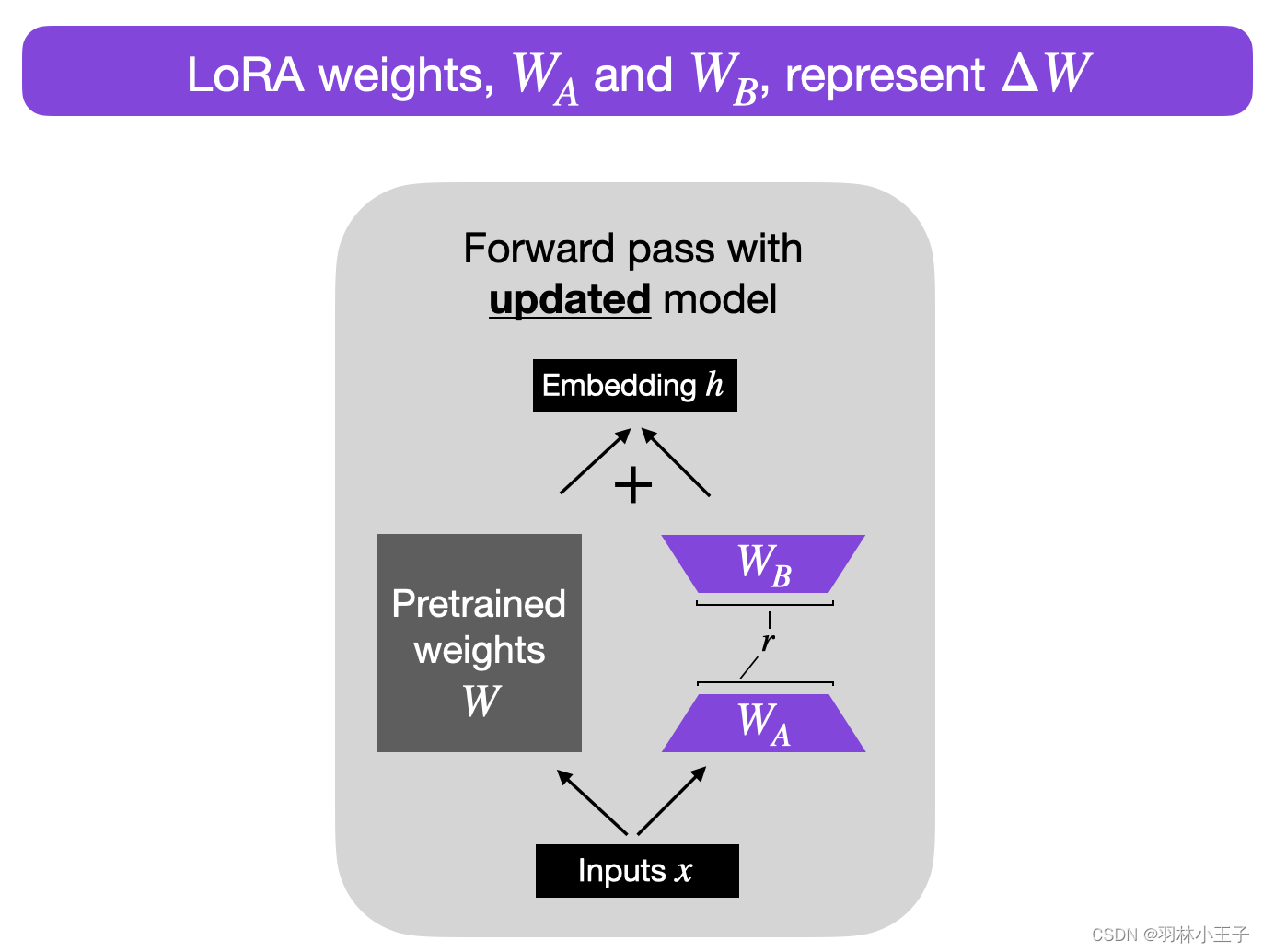
在这里插入图片描述

选择低的秩

上图中的 $r$ 是一个超参数，我们可以用它来指定适应过程中所使用的低秩矩阵的等级。较小的 $r$ 会导致简化的低秩矩阵，从而减少适应过程中需要学习的参数数量。这可以加快训练速度，可能减少计算需求。
然而，较小的 $r$ 会降低低秩矩阵捕捉特定任务信息的能力。这可能导致适应质量较低，模型在新任务上的表现可能不如较高的 $r$ 好。
总结起来，在LoRA中选择较小的 $r$ 存在模型复杂性、适应能力以及欠拟合或过拟合的风险之间的权衡。因此，重要的是尝试不同的 $r$ 值，以找到适合新任务所需性能的合适平衡点。

实现LoRA

LoRA的实现相对简单。我们可以将其视为LLM中全连接层的修改后的前向传播。伪代码如下所示：

input_dim = 768 # 例如，预训练模型的隐藏大小
output_dim = 768 # 例如，层的输出大小
rank = 8 # 低秩适应的等级'r'
W = ... # 来自预训练网络的权重，形状为 input_dim x output_dim
W_A = nn.Parameter(torch.empty(input_dim, rank)) # LoRA权重A
W_B = nn.Parameter(torch.empty(rank, output_dim)) # LoRA权重B初始化LoRA权重
nn.init.kaiming_uniform_(W_A, a=math.sqrt(5))
nn.init.zeros_(W_B)

def regular_forward_matmul(x, W):
	h = x @ W
	return h

def lora_forward_matmul(x, W, W_A, W_B):
	h = x @ W # 常规矩阵乘法
	h += x @ (W_A @ W_B) * alpha # 使用缩放的LoRA权重
	return h