LeetCode977.有序数组的平方

链接：有序数组的平方

给你一个按 非递减顺序 排序的整数数组 nums，返回 每个数字的平方 组成的新数组，要求也按 非递减顺序 排序。

看到这道题，我第一反应就是把每个数的平方算出来然后排序，思路很简单，可以写出如下代码：

public int[] sortedSquares(int[] nums) {
        // 1<=nums.length<=10000
        for(int i=0;i<nums.length;i++){
            nums[i]=nums[i]*nums[i];
        }
        Arrays.sort(nums);
        return nums;
    }

排序的时间复杂度为：O(nlogn)

所以以上代码的时间复杂度是：O(n+nlogn)

空间复杂度：O(1)

虽然能通过这道题，但是有点慢，我看到数组是有序的那么平方后的数字的最大的只有可能在两端出现，所以我们可以用双指针来解这道题，可以写出如下代码：

public int[] sortedSquares(int[] nums) {
        int left=0;
        int right=nums.length-1;
        int[] result=new int[nums.length];
        for(int i=result.length-1;i>=0 && left<=right;i--){
            if(nums[left]*nums[left]>nums[right]*nums[right]){
                result[i]=nums[left]*nums[left];
                left++;
            }else{
                result[i]=nums[right]*nums[right];
                right--;
            }
            
        }
        return result;
    }

时间复杂度：O(n)

空间复杂度：O(n)

测试用例：

1.nums全是正数

2.nums全是负数

3.nums有正有负

4.nums中有重复数字

3.nums为空

LeetCode209.长度最小的子数组

链接：长度最小的子数组

给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其和 ≥ target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

涉及到连续，我们可以考虑用滑动窗口来解这道题

什么是滑动窗口？

滑动窗口就是不断调节起始下标和结束下标，来得到最后的答案，看起来就像一个窗口在滑动一样。

代码如下：

public int minSubArrayLen(int target, int[] nums) {
        // 1 <= nums.length <= 105
        int sum=0;
        int len=0;
        int j=0;
        int result=Integer.MAX_VALUE;
        for(int i=0;i<nums.length;i++){
            sum+=nums[i];
            len++;
            while(sum>=target){
                if(len<result){
                    result=len;
                }
                sum-=nums[j++];
                len--;
            }
        }
        return result==Integer.MAX_VALUE?0:result;
    }

其中i代表结束位置，j代表起始位置，如果sum>=target了，保存长度，并向前移动起始位置，缩短长度，直到sum<target。

滑动窗口的精妙之处在于根据当前子序列和大小的情况，不断调节子序列的起始位置。

时间复杂度：O(n) //虽然for循环里面还有一个while循环，但是只遍历一遍数组所以是O(n）

空间复杂度：O(1)

LeetCode59.螺旋矩阵||

链接：螺旋矩阵||

给你一个正整数 n ，生成一个包含 1 到 n2 所有元素，且元素按顺时针顺序螺旋排列的 n x n 正方形矩阵 matrix 。

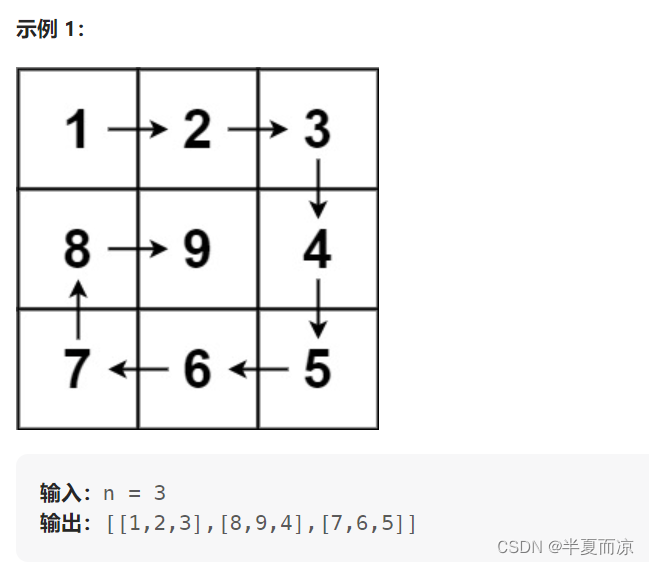
看起来本题很容易，但是就是写不出来，我就是这样，总是有没考虑到的地方，而且代码写的很复杂（一堆判断），最后还是看了题解，本题只需要模拟数字的遍历方向就行，最后写出如下代码：

public int[][] generateMatrix(int n) {
        //1 <= n <= 20
        int loop=0;  //循环次数
        int count=1;  //数字
        int[][] result=new int[n][n];
        int start=0;  //开始点
        int i,j;
        while(loop++<n/2){
            // 左->右
            for(j=start;j<n-loop;j++){
                result[start][j]=count++;
            }
            // 上->下
            for(i=start;i<n-loop;i++){
                result[i][j]=count++;
            }
            // 右->左
            for(;j>=loop;j--){
                result[i][j]=count++;
            }
            // 下->上
            for(;i>=loop;i--){
                result[i][j]=count++;
            }
            start++;
        }
        if(n%2==1){
            result[n/2][n/2]=count;
        }
        return result;
    }