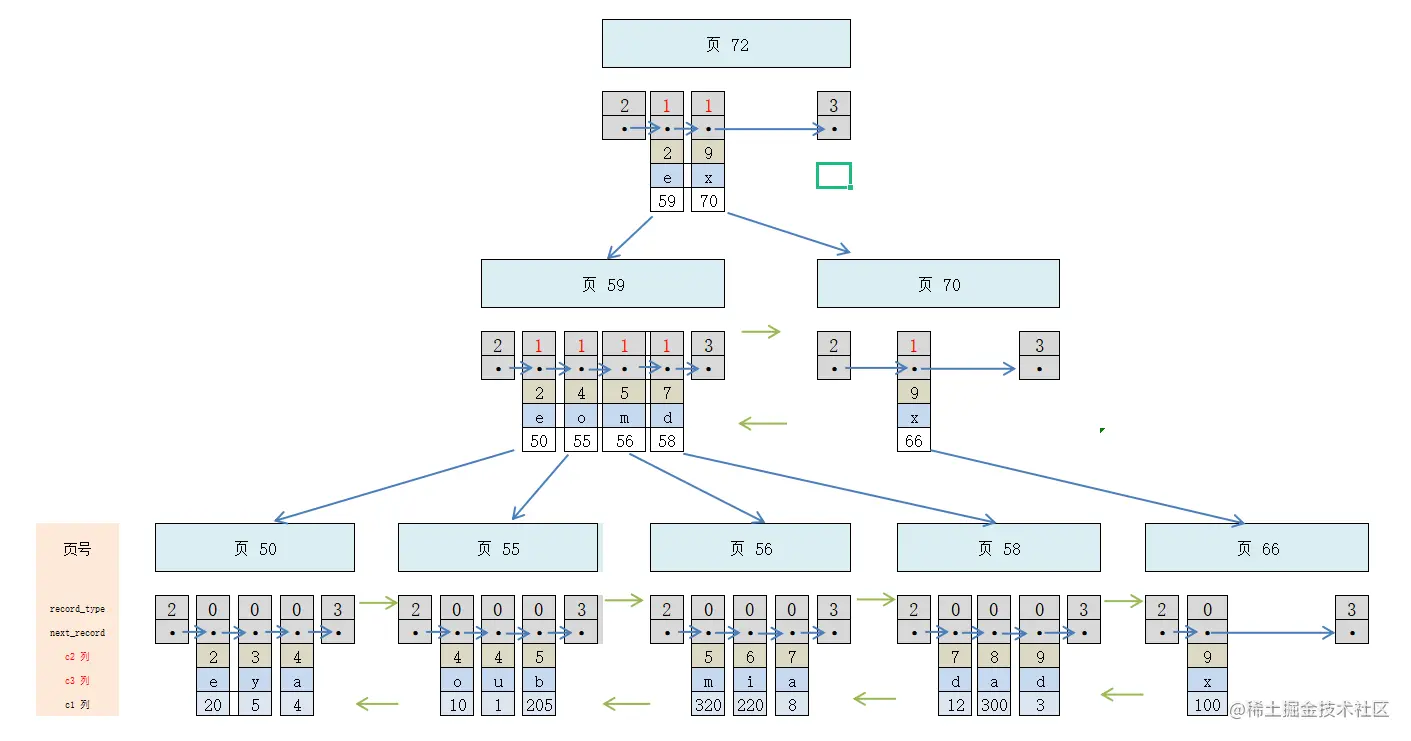
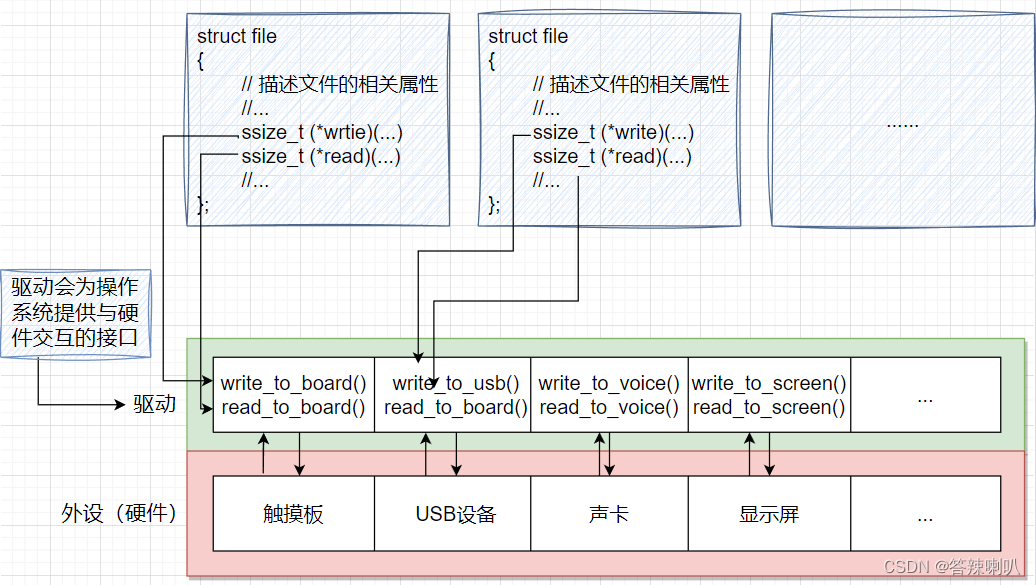
attention机制一直是放在encoder-decoder中进行使用，self-attention是为了解决前者结构无法并行计算，而抽离出的概念（前者的编码解码多为时序网络）。

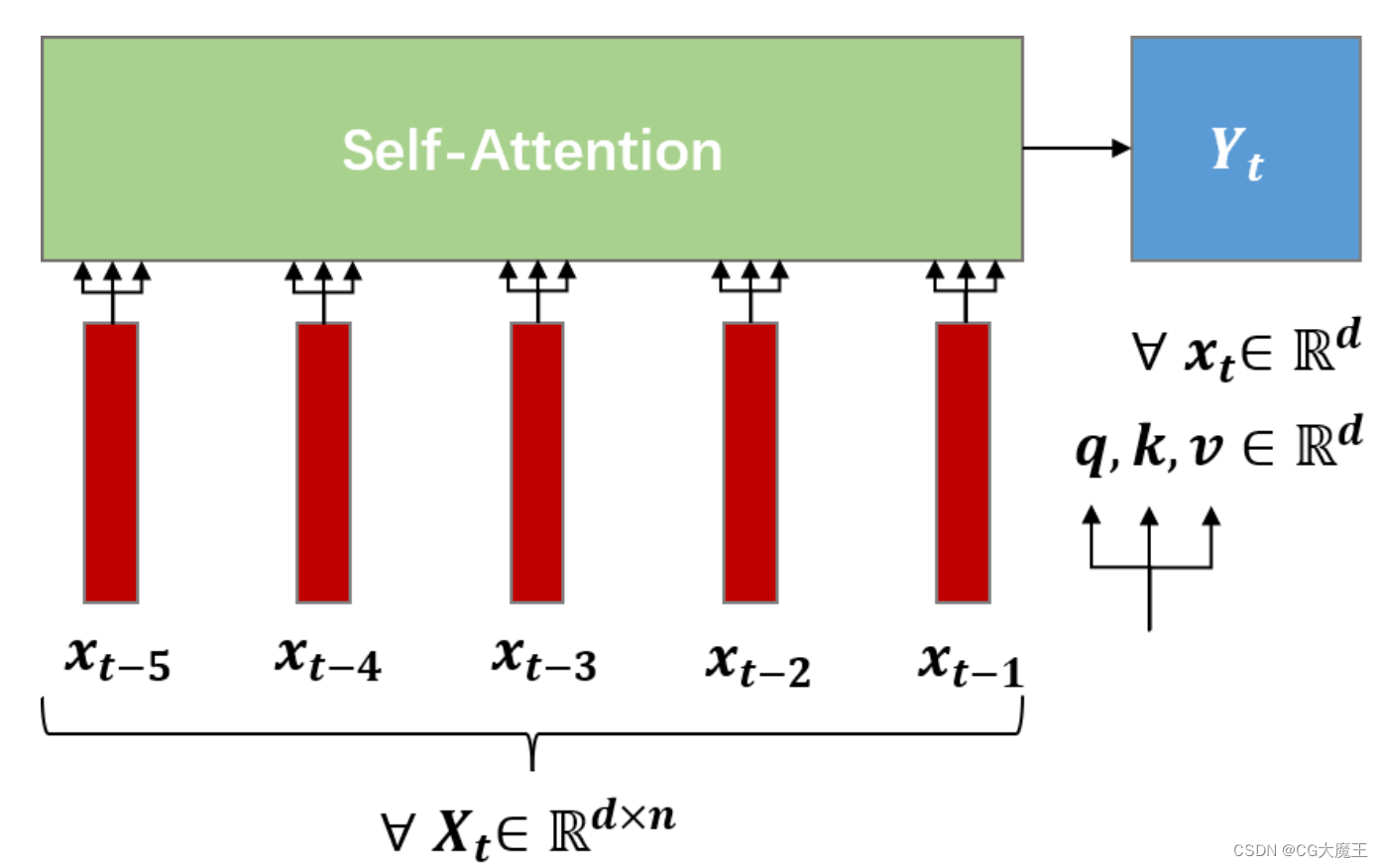
但因为缺少时序模型天然的位置编码特点，所以self-attention模型需要自己嵌入位置编码。

 本着不重复造轮子的态度，自然是先在网上搬运代码，但发现一个奇怪的问题，即我的实验数据词向量维度为偶数的时候，运行正常，但如果词向量维度为奇数，则无法运行，会报如下错误：

# The expanded size of the tensor (i) must match the existing size (i+1) at non-singleton dimension 2.  Target sizes: [batch_size, seq_len, i].  Tensor sizes: [seq_len, i+1]    

因为对应不同人的数据不一致，所以这里用i代替具体数据，batch_size, seq_len同理。

而导致这个报错的原因是，因为常见的位置编码方式（如下图），在编码的时候，是先生成一个由2j构成的矩阵，j∈d_model，d_model为词向量维度。

 因为直接口述相对抽象，这里先展示源码，然后在根据代码说明。

类的输入数据尺寸为（batch_size，seq_len，d_model）

class PositionalEncoding(nn.Module):
    """位置编码
    d_model: 特征维度
    max_len: 序列长度
    dropout:是为了防止对位置编码太敏感
    """
    def __init__(self, d_model, max_len=10, dropout=0):
        super(PositionalEncoding, self).__init__()
        self.dropout = nn.Dropout(dropout)
        # 创建一个足够长的P
        self.P = torch.zeros((1, max_len, d_model))
        position = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1)
        div_term = torch.pow(10000, torch.arange(0, d_model, 2, dtype=torch.float32) / d_model)
        X = position / div_term
        # P[[:, :, 0::2]这个用法,就是从0开始到最后面,步长为2,代表的是偶数位置
        self.P[:, :, 0::2] = torch.sin(X)
        # self.P[:, :, 1::2] = torch.cos(X)
        if d_model % 2 == 0:
            self.P[:, :, 1::2] = torch.cos(X)
        else:
            self.P[:, :, 1::2] = torch.cos(X)[ :, :-1]

    def forward(self, X):
        X = X + self.P[:, :X.shape[1], :].to(X.device)
        return self.dropout(X)

 根据上面公式可以发现，sin和cos的括号中，参与计算的数据是一样的(也就是上文中提到的生成的2j矩阵)，在代码中，该数据由下列代码生成：

        position = torch.arange(max_len, dtype=torch.float32).reshape(-1, 1)
        div_term = torch.pow(10000, torch.arange(0, d_model, 2, dtype=torch.float32) / d_model)
        X = position / div_term

其中，position为公式中的分子，div_term为分母，根据div_term中的arrange可以看出步长为2，也就对应2j，而这导致一个什么结果呢？

即

d_model=3，生成的二维矩阵X的第二维为2;

d_model=4，生成的二维矩阵X的第二维为2;

d_model=5，生成的二维矩阵X的第二维为3;

d_model=6，生成的二维矩阵X的第二维为3.

第一维为seq_len

我们再看看self.P，其尺寸为(1, seq_len, d_model)

        
        # P[[:, :, 0::2]这个用法,就是从0开始到最后面,步长为2
        self.P[:, :, 0::2] = torch.sin(X)
        # self.P[:, :, 1::2] = torch.cos(X)
        if d_model % 2 == 0:
            self.P[:, :, 1::2] = torch.cos(X)
        else:
            self.P[:, :, 1::2] = torch.cos(X)[ :, :-1]

这里通过 P[[:, :, x::2]中x为0还是1来控制奇数还是偶数，但当P中d_model为奇数的时候，cos那行等式左右两个矩阵大小就不一致了。

以d_model=5举例

此时X = [seq_len， 3]，torch.cos(X)为[seq_len， 3],

而self.P[:, :, 1::2] 的维度为[1, seq_len, 2]

上式是将右侧二维矩阵赋给左侧三维矩阵的后两维，但此时两者尺寸并不满足条件，cos注释部分为网上找到的源码，下面为改进方法，其实思路很简单，就是先对d_model做一个奇偶判断，当我们输入数据的词向量维度为奇数的时候，我们不取最后一维的最后一个值即可。