1.非线性特征

当数据位于一个薄饼状的线性子空间时，PCA 是非常有用的。但如果数据形成了一个更加复杂的形状，情况又将如何呢？
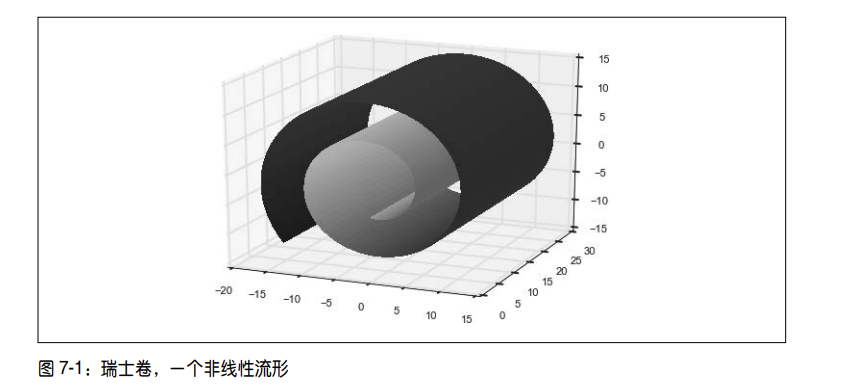
在这里插入图片描述

如果线性子空间是一张平展的纸，那么非线性流形的一个简单例子就是卷起来的纸，它有
个非正式的名称，叫作瑞士卷。一旦卷了起来，二维平面就占据了三维空间，尽管它本质上还是个二维对象。换句话说，它具有低本征维数。如果能够以某种方式展开瑞士卷，就可以恢复二维平面。这就是非线性数据降维的目标，它假定流形要比它所在的全维度空间简单，然后试图将其展开。

流形能够展开的关键在于，即使一个大的流形看上去非常复杂，但它的每个数据点的邻近区域通常可以非常好地近似为一块平面。换句话说，可以通过多个小平面使用局部结构组成全局结构。非线性数据降维也称为非线性嵌入或流形学习。非线性嵌入可以非常有效地将高维数据压缩为低维数据，常用于二维空间或三维空间中的可视化。

但是，尽量降低特征维度只是特征工程目标的一小部分，它的根本目标还是为当前任务找
到正确的特征。

聚类算法通常不被用作局部结构学习技术，但实际上它完全可以胜任。彼此相近（可以用一种特定的度量方式来定义“近”的概念）的点属于同一个簇。给定一个聚类，数据点可以用它的簇成员向量来表示。如果簇的数量小于初始的特征数量，那么相对于初始表示，这种新表示就具有更少的维度，初始数据就被压缩进一个更低维度的空间。

2.模型堆叠

核心思想:先使用复杂的基础层（通常带有昂贵的模型）生成良好的（通常是非线性的）特征，再与简单快速的顶层模型组合起来。这样通常能实现模型准确率和速度之间的正确平衡，即多个模型的堆叠。

3.K均值聚类过程

下列代码展示了在两种不同的、随机生成的数据集上的 k-均值聚类。(a) 中的数据是使用几种随机高斯分布生成的，这些分布的方差相同但均值不同。© 中的数据则是完全随机生成的。这些用于实验的问题非常容易解决，k-均值聚类的效果非常好。（聚类结果对簇的数目非常敏感，簇数目必须在算法中给定。）

import numpy as np
from sklearn.cluster import KMeans
from sklearn.datasets import make_blobs

import matplotlib.pyplot as plt
import seaborn as sns
%matplotlib notebook

n_data = 1000
seed = 1
n_centers = 4

# 生成符合高斯分布的数据
blobs, blob_labels = make_blobs(n_samples=n_data, n_features=2, 
                                centers=n_centers, random_state=seed)
# 运行算法
clusters_blob = KMeans(n_clusters=n_centers, random_state=seed).fit_predict(blobs)# 聚类是直接训练并分好类

# 生成完全随机的数据
uniform = np.random.rand(n_data, 2)
clusters_uniform = KMeans(n_clusters=n_centers, random_state=seed).fit_predict(uniform)

figure = plt.figure(figsize=(20,10))
plt.subplot(221)
plt.scatter(blobs[:, 0], blobs[:, 1], c=blob_labels, edgecolors='k', cmap='PuRd')
plt.title("(a) Four randomly generated blobs", fontsize=14)
plt.axis('off')

plt.subplot(222)
plt.scatter(blobs[:, 0], blobs[:, 1], c=clusters_blob, edgecolors='k', cmap='PuRd')
plt.title("(b) Clusters found via K-means", fontsize=14)
plt.axis('off')

plt.subplot(223)
plt.scatter(uniform[:, 0], uniform[:, 1], edgecolors='k')
plt.title("(c) 1000 randomly generated pois", fontsize=14)
plt.axis('off')

plt.subplot(224)
plt.scatter(uniform[:, 0], uniform[:, 1], c=clusters_uniform, edgecolors='k', cmap='PuRd')
plt.title("(d) Clusters found via K-means", fontsize=14)
plt.axis('off')

在这里插入图片描述

4.使用K聚类进行非线性特征(曲面/非平面)的降维

使用K聚类对非线性特征（比如曲面性特征）的聚类，得到输出，作为下一个模型的输入。

一般的聚类应用假定在数据中可以找到自然形成的簇，也就是说，空间中分布着一些密集
数据区域，空间的其他部分则相对空旷。在这种情况下，需要确定正确的簇数目，而为了
选择这个 k，人们发明了聚类索引来测量数据分组的质量。

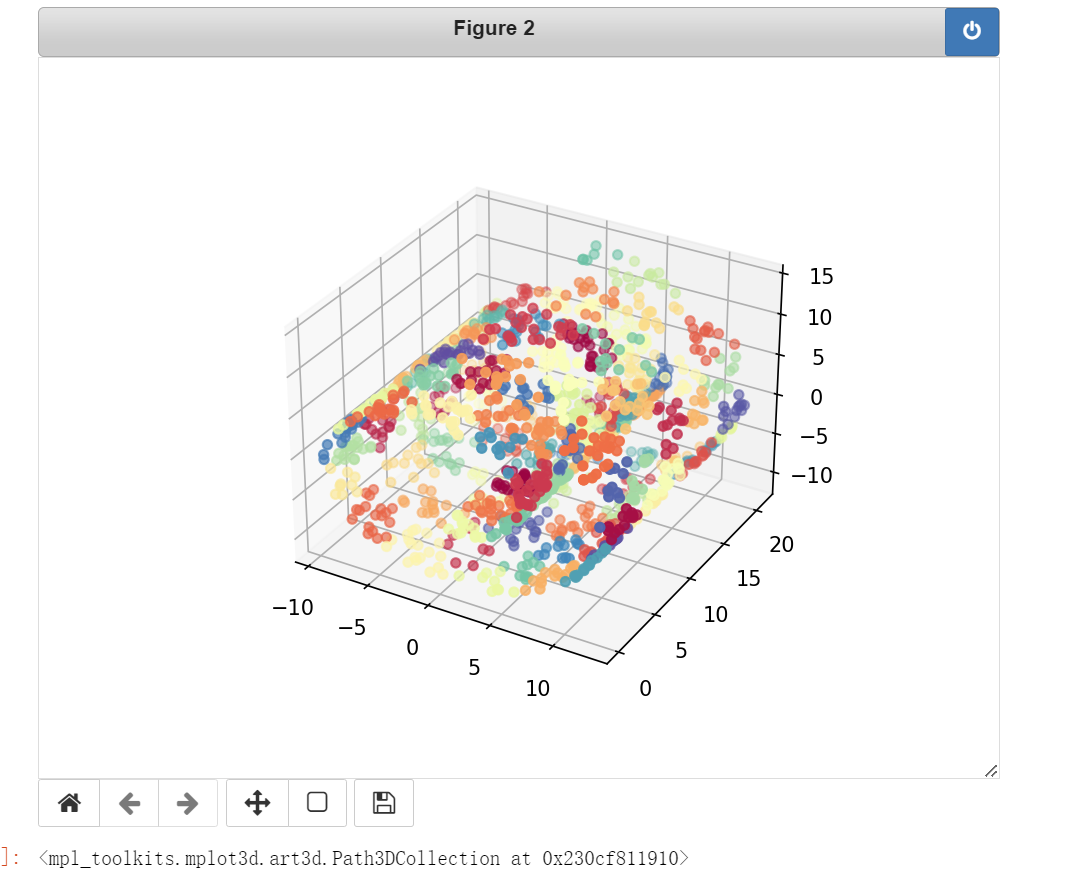
使用 scikit-learn 在瑞士卷上生成了一个带噪声的数据集，对其使用 k-均值算法进行了
聚类，并使用 Matplotlib 对聚类结果进行了可视化。数据点按照它们的簇 ID 进行了着色。

from mpl_toolkits.mplot3d import Axes3D
from sklearn import manifold
from sklearn.datasets import make_swiss_roll

# 生成带噪声的非线性数据集(例如卷状)
X, color = make_swiss_roll(n_samples=1500)

# 使用100个k-均值簇对数据进行近似: 聚成100个类，当然，实际上可以使用交叉验证或者重复K
clusters_swiss_roll = KMeans(n_clusters=100, random_state=seed).fit_predict(X)
# 曲面数据的聚类无疑就是增加簇的个数

fig2 = plt.figure()
ax = fig2.add_subplot(111, projection='3d')
ax.scatter(X[:, 0], X[:, 1], X[:, 2], c=clusters_swiss_roll, cmap='Spectral')

在这里插入图片描述

5.用于分类问题的K均值特征化(模型堆叠)

聚类算法可以分析数据的空间分布，因此，k-均值特征化可以生成数据的压缩空间索引，供下一阶段的模型使用。这就是模型堆叠的一个例子。

如果还有目标变量，那么也可以将目标变量中的信息作为聚类过程的提示。加入目标变量信息的一种方法是，直接将目标变量作为 k-均值算法的一个额外输入特征。因为我们的目标是将所有输入维度上的欧氏距离的总和最小化，所以聚类过程除了在初始特征空间中以外，也会在目标变量值之间平衡相似度。可以对目标变量进行缩放，来增加或减少聚类算法对它的关注程度。目标变量之间的差距较大时，会生成更加注重分类边界的簇。

可以有选择地为 k-均值提供类标签作为输入，这有助于 k-均值找到与类别边界更加对齐的簇。

（1）构造K均值特征

import numpy as np
from scipy.spatial import Voronoi, voronoi_plot_2d
from sklearn.cluster import KMeans
from sklearn.datasets import make_moons
from sklearn.preprocessing import OneHotEncoder
import sklearn
import scipy

import matplotlib.pyplot as plt
%matplotlib notebook

class KMeansFeaturizer:
    """将数值数据转换为k-means集群成员.
    
    这个转换器对输入数据运行k-means，并将每个数据点转换为最近集群的id。
    如果存在一个目标变量，则将其作为k-means的输入进行缩放，以导出遵从分类边界的簇，并将相似点分组在一起。.

    Parameters
    ----------
    k: integer, optional, default 100;
        将数据分组到的集群的数量。.

    target_scale: float, [0, infty], optional, default 5.0
                目标变量的比例因子。将其设置为零则忽略目标。对于分类问题，较大的“target_scale”值将产生更好地尊重类边界的集群。

    random_state : integer or numpy.RandomState, optional
                    它被传递给k-means作为初始化kmeans中心的生成器。如果给定一个整数，它会修复种子。默认为全局numpy随机数生成器。

    Attributes
    ----------
    cluster_centers_ : array, [k, n_features]
        集群中心坐标。n_features对目标列进行计数。
    """

    def __init__(self, k=100, target_scale=5.0, random_state=None):
        self.k = k
        self.target_scale = target_scale
        self.random_state = random_state
        self.cluster_encoder = OneHotEncoder().fit(np.array(range(k)).reshape(-1,1))
        
    def fit(self, X, y=None):
        """对输入数据运行k-means并找到质心。

        如果没有给定目标(' y '为None)，那么在输入' X '上运行普通的k-means。

        如果给定了目标' y '，那么包括目标(由' target_scale '加权)作为k-means聚类的额外维度。
        在这种情况下，运行两次k-means，第一次运行目标，然后再运行一次没有目标的额外迭代。

        拟合后，属性' cluster_centers_ '被设置为输入空间中由' X '表示的k-means中心。

        Parameters
        ----------
        X : array-like or sparse matrix, shape=(n_data_points, n_features)

        y : 长度为n_data_points的向量，可选，默认None;
            如果提供，将用“target_scale”进行加权，并包含在k-means集群中作为提示。
        """
        if y is None:
            # 不用目标变量，只用k均值
            km_model = KMeans(n_clusters=self.k, 
                              n_init=20, 
                              random_state=self.random_state)
            km_model.fit(X)

            self.km_model_ = km_model
            self.cluster_centers_ = km_model.cluster_centers_
            return self

        # 有目标信息。应用适当的缩放并将其包含到k-means的输入数据中         
        data_with_target = np.hstack((X, y[:,np.newaxis]*self.target_scale))

        # 在数据和标签上建立K-means模型。
        km_model_pretrain = KMeans(n_clusters=self.k, 
                                   n_init=20, 
                                   random_state=self.random_state)
        km_model_pretrain.fit(data_with_target)

        # 运行k-means--第二次在没有目标信息的情况下在原始空间中获取集群。使用训练前发现的中心进行初始化。
        # 通过单一的聚类分配迭代和质心重新计算。
        km_model = KMeans(n_clusters=self.k, 
                          init=km_model_pretrain.cluster_centers_[:,:2], 
                          n_init=1, 
                          max_iter=1)
        km_model.fit(X)
        
        self.km_model = km_model
        self.cluster_centers_ = km_model.cluster_centers_
        return self
        
    def transform(self, X, y=None):
        """为每个输入数据点输出最近的集群id。

        Parameters
        ----------
        X : array-like or sparse matrix, shape=(n_data_points, n_features)

        y : vector of length n_data_points, optional, default None
            标签向量被忽略，即使提供。

        Returns
        -------
        cluster_ids : array, shape[n_data_points,1]
        """
        clusters = self.km_model.predict(X)
        return self.cluster_encoder.transform(clusters.reshape(-1,1))
    
    def fit_transform(self, X, y=None):
        """运行fit之后是transform转换特征。
        """
        self.fit(X, y)
        return self.transform(X, y)

生成数据

seed = 1
training_data, training_labels = make_moons(n_samples=2000, noise=0.2, random_state=seed)

进行特征转换,可以使用transform()方法获取到转换后的特征数据。

kmf_hint = KMeansFeaturizer(k=100, target_scale=10, random_state=seed).fit(training_data, training_labels)
kmf_no_hint = KMeansFeaturizer(k=100, target_scale=0, random_state=seed).fit(training_data, training_labels)

绘制数据

def kmeans_voronoi_plot(X, y, cluster_centers, ax):
    """绘制覆盖数据的kmeans集群的Voronoi图"""
    ax.scatter(X[:, 0], X[:, 1], c=y, cmap='Set1', alpha=0.2)
    vor = Voronoi(cluster_centers)
    voronoi_plot_2d(vor, ax=ax, show_vertices=False, alpha=0.5)
fig = plt.figure()
ax = plt.subplot(211, aspect='equal')
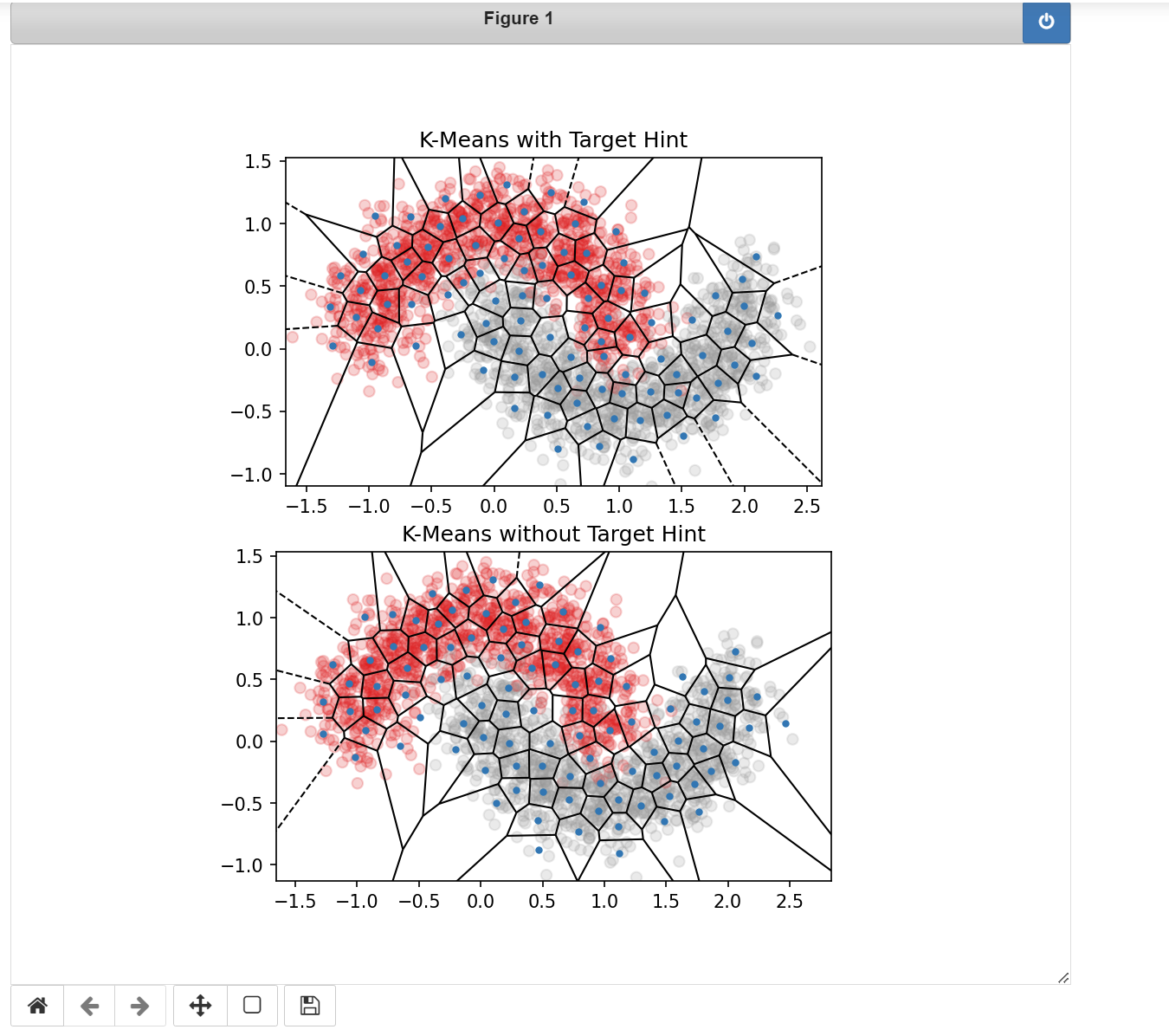
kmeans_voronoi_plot(training_data, training_labels, kmf_hint.cluster_centers_, ax)
ax.set_title('K-Means with Target Hint')
# 使用目标类信息的 k-均值聚类

ax2 = plt.subplot(212, aspect='equal')
kmeans_voronoi_plot(training_data, training_labels, kmf_no_hint.cluster_centers_, ax2)
ax2.set_title('K-Means without Target Hint')
# 不使用目标类信息的 k-均值聚类

在这里插入图片描述
如何获取到K均值转换后的特征数据呢？
可以使用transform()方法或者fit_transform方法获取。可以有选择地为 k-均值提供类标签作为输入，这有助于 k-均值找到与类别边界更加对齐的簇。

model = KMeansFeaturizer(k=100, target_scale=10, random_state=seed)
model.fit(training_data,training_labels)
# 这里new_x就是聚类后的数据
new_x = model.transform(training_data).toarray()
new_x,new_x.shape

（2）查看K均重特征对分类问题的效果

# 测试一下 k-均值特征对于分类问题的有效性。

# 使用与训练数据相同的分布生成一些测试数据
test_data, test_labels = make_moons(n_samples=2000, noise=0.3, random_state=seed+5)

# 使用k-均值特征生成器生成簇特征
training_cluster_features = kmf_hint.transform(training_data)
test_cluster_features = kmf_hint.transform(test_data)

# 使用簇特征构造新的输入特征
training_with_cluster = scipy.sparse.hstack((training_data, training_cluster_features))#矩阵拼接
test_with_cluster = scipy.sparse.hstack((test_data, test_cluster_features))

# 建立分类器
from sklearn.linear_model import LogisticRegression
from sklearn.svm import SVC
from sklearn.neighbors import KNeighborsClassifier
from sklearn.ensemble import RandomForestClassifier, GradientBoostingClassifier

lr_cluster = LogisticRegression(random_state=seed).fit(training_with_cluster, training_labels)#使用簇特征训练LR模型


# 使用没有进行K均值聚类特征化的数据进行训练模型，即使用原数据。
classifier_names = ['LR',
                    'kNN',
                    'RBF SVM',
                    'Random Forest',
                    'Boosted Trees']
classifiers = [LogisticRegression(random_state=seed),
               KNeighborsClassifier(5),
               SVC(gamma=2, C=1, random_state=seed),
               RandomForestClassifier(max_depth=5, n_estimators=10, 
                                      max_features=1, random_state=seed),
               GradientBoostingClassifier(n_estimators=10, learning_rate=1.0,
                                          max_depth=5, random_state=seed)]
for model in classifiers:
    model.fit(training_data, training_labels)

# 使用ROC评价分类器性能的辅助函数
def test_roc(model, data, labels):
    if hasattr(model, "decision_function"):
        predictions = model.decision_function(data)
    else:
        predictions = model.predict_proba(data)[:,1]
    fpr, tpr, _ = sklearn.metrics.roc_curve(labels, predictions)
    return fpr, tpr

# 绘制结果
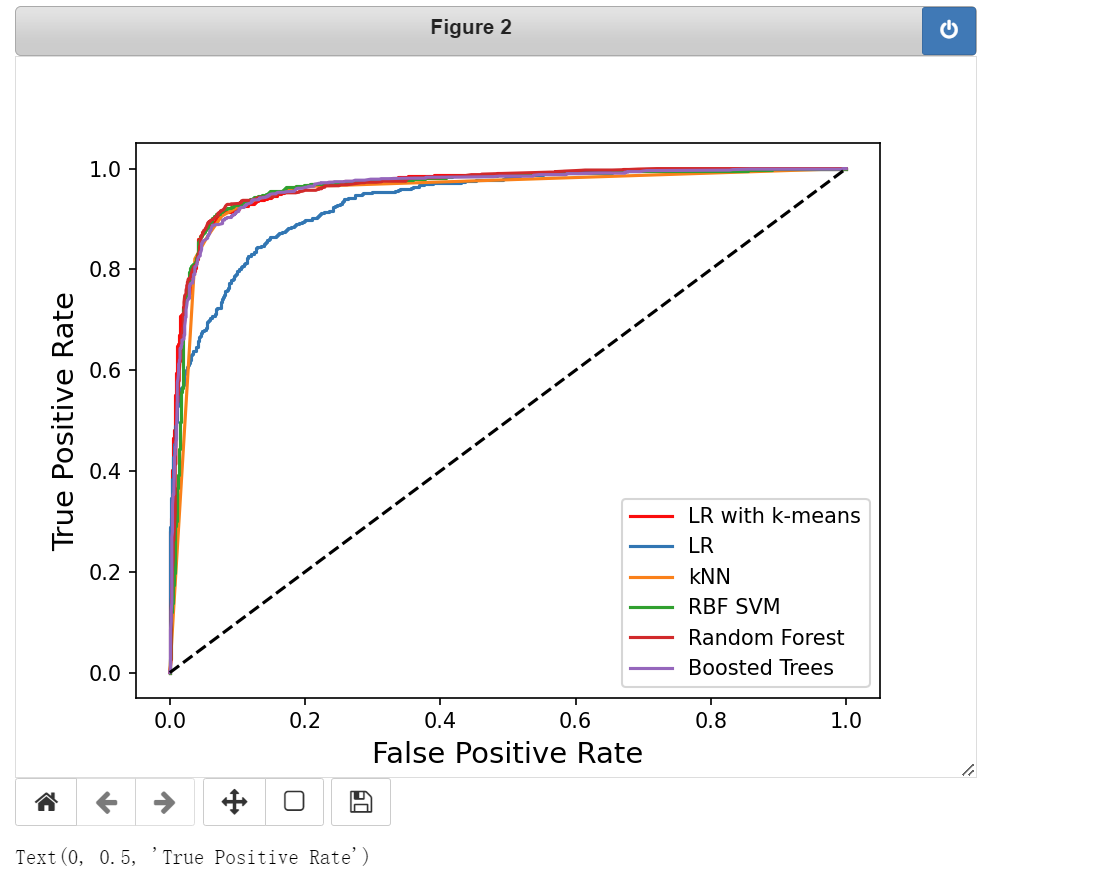
plt.figure()
fpr_cluster, tpr_cluster = test_roc(lr_cluster, test_with_cluster, test_labels)
plt.plot(fpr_cluster, tpr_cluster, 'r-', label='LR with k-means')

for i, model in enumerate(classifiers):
    fpr, tpr = test_roc(model, test_data, test_labels)
    plt.plot(fpr, tpr, label=classifier_names[i])
    
plt.plot([0, 1], [0, 1], 'k--')
plt.legend()
plt.xlabel('False Positive Rate', fontsize=14)
plt.ylabel('True Positive Rate', fontsize=14)
# 一个好的分类器应该能快速地达到很高的真阳性率和很低的假阳性率，所以，能快速靠近左上角的曲线是极好的。

在这里插入图片描述

6.密集向量特征化(可以使用更小的K)

如果不使用 one-hot 编码的簇隶属关系，还可以使用一个密集向量来表示数据点，这个向量由数据点到每个簇中心点距离的倒数组成。相对于简单的二值化簇分配，这种方式可以保留更多的信息，只不过表示方式是密集的。这就是一种妥协。one-hot 编码的簇隶属关系可以提供一种非常轻量的、稀疏的表示，但需要一个比较大的 k 值来表示形状复杂的数据。距离倒数表示法是密集的，对于建模的各个步骤来说代价更高，但优点是可以使用更小的 k。

稀疏表示和密集表示之间的一种折中方案是，只保留 p 个最近簇的距离倒数。但这样一
来，又多了一个需要调优的超参数 p。（现在你能理解为什么特征工程需要考虑这么多细节
了吧？）世间没有免费的午餐。

7.优点、缺点以及陷阱

使用 k-均值将空间数据转换为特征是模型堆叠的一个实例，其中一个模型的输入是另一个模型的输出。另一个堆叠实例是使用决策树类型模型（随机森林或梯度提升树）的输出作为线性分类器的输入。

近年来，模型堆叠已经成为了一种越来越流行的技术，因为训练和维护非线性模型的成本非常高昂。堆叠的核心思想是将非线性放入特征中，再使用一种非常简单的、通常是线性的模型作为最后一层。特征生成器可以在线下训练，这意味着我们可以使用昂贵的、需要更多计算能力和内存的模型来生成有用的特征。位于顶层的简单模型可以快速适应在线数据中快速的分布变化。这是一种精确度和速度之间的权衡，这种策略通常使用在像定向广告这样需要快速适应数据分布变化的应用中。

核心思想：先使用复杂的基础层（通常带有昂贵的模型）生成良好的（通常是非线性的）特征，再与简单快速的顶层模型组合起来。这样通常能实现模型准确率和速度之间的正确平衡。

与使用非线性分类器相比，k-均值与逻辑回归的堆叠模型更容易训练和存储。表 7-1 详细列出了一些机器学习模型在计算能力和内存方面的训练和预测复杂度。n 表示数据点的数量，d 表示（初始）特征的数量。
在这里插入图片描述
k-均值特征化适合实数型、有界的、能在空间中形成块状密集区域的数值特征。块状区域
可以是任意形状，因为我们可以增加簇的数量来近似它们。（与经典聚类方法不同，我们
不关心如何找出簇的“真实”数目，而只需覆盖它们。）k-均值不能处理欧氏距离无效的特征空间，即分布奇特的数值型变量或分类变量。如果特征集合中包括这种变量，那么有以下几种处理方法。