目录

一，核函数的引入

二，核函数的定义

三，核函数介绍：

四，核函数总结：

---

一，核函数的引入

世界上本来没有两个完全一样的物体，对于所有的两个物体，我们可以通过增加维度来让他们最终有所区别，比如说两本书，从(颜色，内容)两个维度来说，可能是一样的，我们可以加上作者这个维度，实在不行我们还可以加入页码，可以加入拥有者，可以加入购买地点，可以加入笔记内容等等。当维度增加到无限维的时候，一定可以让任意的两个物体可分了.

一般对于低维线性不可分的数据，在映射到高位以后，就变成了线性可分的，为此通过核函数将低维的数据映射到高维，再次利用SVM进行分类的思想。

回顾线性可分SVM的优化目标

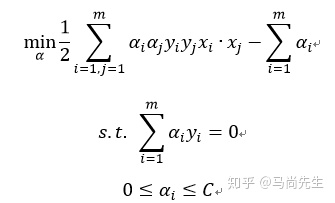
低维特征仅仅以内积 xi∙xj 的形式出现，假如定义一个低维到高维特征空间的映射 ∅ ，将所有的特征映射到一个更高的维度，使数据线性可分，此时继续的使用线性可分的优化目标，求出分离超平面和分类决策函数。也就是说现在的SVM优化目标变为：

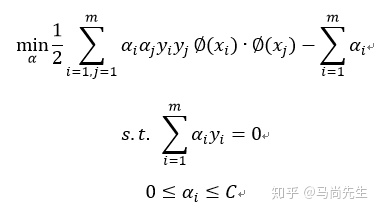
优化目标只是将内积 xi∙xi 换成 ∅(xi)∙∅(xj) 。

问题又出现了：

看起来似乎解决了问题，原始的空间为三维可以映射到20维，这也可以处理，但是我们低维的特征是100个维度，那需要更高的维度来映射，这时候映射成的高维度是爆炸性增长的，计算量太大，无法计算了。这时候就是核函数真正发挥威力的地方，先来就看下核函数的定义。

二，核函数的定义

假设 ∅ 是一个从低维的输入空间X（欧式空间的子集或是离散集合）到高维的希尔伯特空间H的映射，那么存在函数K(x,z)对任意x和z属于空间X，都有：

就称K(x,z) 为核函数。仔细观察上式可以发现，K(x,z)的计算是在低维特征空间来计算的，它避免了在刚才我们提到了在高维维度空间计算内积的恐怖计算量。也就是说，我们可以好好享受在高维特征空间线性可分的红利，却避免了高维特征空间恐怖的内积计算量。

三，核函数介绍：

核函数必须满足的条件，函数任何点的集合形成的Gram矩阵都是半正定的，即对于任意的 xi∈X,i=1,2,3…m.k(xi,xj) 对应的Gram矩阵 K=[k(xi,xj)] 是半正定矩阵，则K(x,z)是正定核函数。

常用的核函数有：

1，线性核函数(Linear Kernel)：

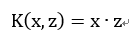
也就是说，线性可分的SVM和线性不可分的SVM是一类的，仅仅在于核函数的不同。,

2，多项式核函数（Polynomial Kernel）：

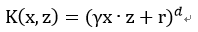
其中的参数都需要在实际的工程中进行调节。

3，高斯核函数（Gaussian kernel），也称之为径向基核函数，是非线性分类SVM的最主流函数：

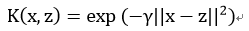
其中， γ 大于0，需要调节的参数。

4，Sigmoid 核函数：

总结下SVM 核函数的求解过程

1）构造服从约束的目标函数

2）用SMO算法求出上式最小时对应的 α 向量的值 α∗ 向量

3）计算 w∗=∑i=1mαi∗yixi

4) 找出所有的S个支持向量，即满足 0≤αi≤C 对应的样本 （）（xs,ys） ，通过

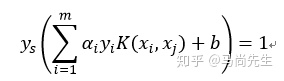
计算出每个支持向量 （）（xs,ys） 对应的 bs∗=ys−∑i=1mαiyiK(xi,xj) ，所有的 bs∗ 对应的平均值即为最终的 b∗=1/s∑i=1sbs∗

这样最终的分类超平面和决策函数为：

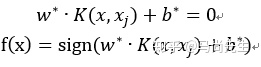
四，核函数总结：

核函数的本质就是，将低维的样本特征映射到高维，使原本线性不可分的样本，线性可分可以继续的使用SVM模型。核函数的价值在于它虽然也是将特征进行从低维到高维的转换，但核函数好在它在低维上进行计算，而将实质上的分类效果（利用了内积）表现在了高维上，这样避免了直接在高维空间中的复杂计算，真正解决了SVM线性不可分的问题。

参考文献：

支持向量机SVM核函数研究 - 知乎