引言

MIT6.042（计算机科学中的数学）是MIT 的离散数学以及概率综合课程，导师是大名鼎鼎的 Tom Leighton ( Akamai 的联合创始人之一)。学完之后对于后续的算法学习大有裨益。

强归纳法

我们平时常用的归纳法证明分为两步（假设P_n表示变量为n时命题成立）：

第一步：考虑基准情况，一般是P₀或P₁。
第二步：假设P_n成立，证明P_n+1成立。

强归纳法与归纳法类似，它也分为两步：

第一步：与归纳法相同，考虑基准情况。
第二步：假设P₀，P₁，…，P_n都成立，证明P_n+1成立。

举个例子来说明强归纳法的应用。

例题：拆积木游戏

每次将叠在一起的多块积木拆成两叠，得到的分数为两叠积木的数量乘积。例如：
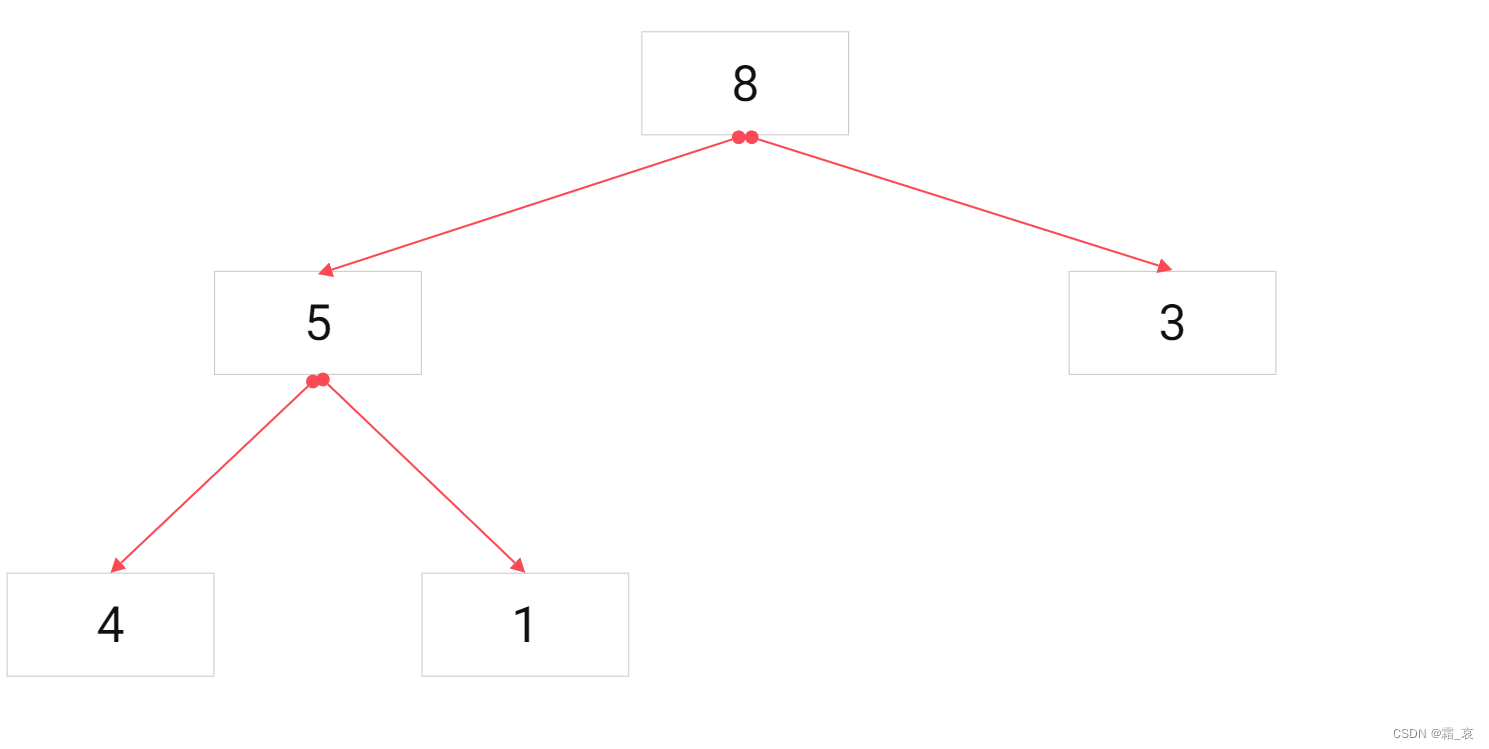
在这里插入图片描述
在第一次拆分时，将叠在一起的8块积木拆分成5块的一叠和3块的一叠，得到53=15分；第二次拆分时，将5块的一叠拆分成4块和1块，得到41=4分…如此重复，直到分成八叠一块的积木，分无可分为止，将每次拆分得到的分数相加，就是最后得到的分数。
尝试不同的拆分8块积木的方式，你会发现最后得到的分数都相同。扩展这一特例，我们可以证明：用所有方式拆分n块积木，最后得到的分数都相同。

证明

我们可以用强归纳法来证明。首先，我们需要猜测P_n等于多少。列举P₁,P₂,P₃等例子，我们猜测P_n=n（n-1）/2。（注意：这里有一个强化归纳假设的技巧，我们可以通过证明更强、更明确的归纳假设来证明想要证明的命题），于是，我们转而证明拆分n块积木会得到n（n-1）/2分。

基准情况：P₀已经计算过，满足命题。
归纳步骤：如果P₁，P₂，…，P_n都成立，那么证明P_n+1成立。

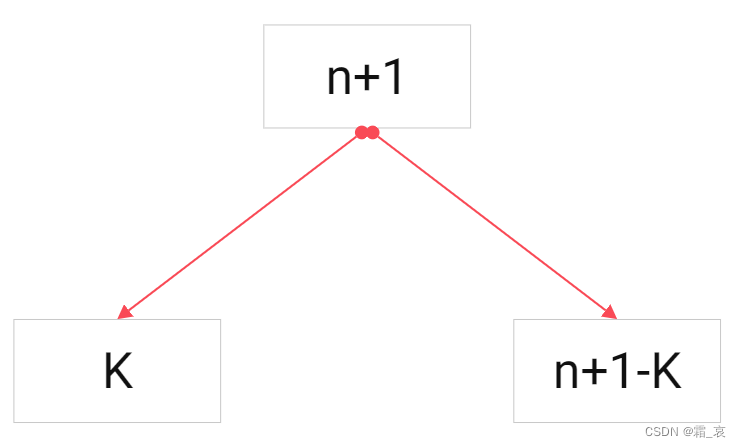
如图所示，不失一般性地，可以将n+1块积木拆成K块积木和n+1-K块积木。那么：

P_n+1
=K(n+1-K)+P_K（拆分K块积木最后能得到的总分数）+P_n+1-K（拆分n+1-K块积木得到的总分数）
=K（n+1-K）+K(K-1)/2+(n+1-K)(n-K)/2
=(n+1)n/2 □（这个符号代表证明结束）

总结：当推导P_n+1时不仅需要P_n，P_n-1，也需要从P₀到P_n的不确定值时，就需要用强归纳法来证明。

数论（第一节）

整除运算

定义：如果m能整除a，则我们说m|a（注意，和正常除法的顺序相反）。

例题：取水

证明：用一个A加仑的水箱和一个B加仑的水箱量出指定加仑的水，则我们能准确量出的水的加仑数不大于A或B且拥有A和B的最大公约数作为约数。

证明

设A和B的最大公约数为m，我们用（x，y）来表示两个水箱中分别存储的水，则我们需要证明m|x且m|y。我们用归纳法来证明：

基准情况：一开始水箱中没有水，即（0，0），显然符合命题。
归纳步骤：设n步后水箱中为（x，y）符合命题，那么n+1步后可能有如下几种情况：

（0，y）、（x，0）、（a，y）、（a，b）、（x，b）
当x+y<=b时，可以到达（0，x+y）
当x+y<=a时，可以到达（x+y，0）
当x+y>=b时，可以到达（x+y-b，b）
当x+y>=a时，可以到达（a，x+y-a）

不难证明这些情况都拥有m这个约数。□

公约数

定义：A和B的最大公约数称为gcd（A，B）

例题

证明定理：用上面的两个水箱可以量出所有不大于A和B且能被A和B线性变换得到的数。

证明

我们直接给出满足上述定理的算法（不失一般性地，假设A<B）：

装满A加仑的水箱
将A水箱中的水加入B水箱
如果B水箱被装满了，倒掉B中的水，返回第2步
如果没有得到想要的加仑数，返回第1步

接下来我们证明这个算法：

在这个算法中，假设我们充满m次A加仑水箱，倒掉n次B加仑水箱，得到r加仑水，则r=mA-nB。设L=mA+qB，那么
r=mA+qB-qB-nB=L-（q+n）B。由于r和L都是正数且小于B，因此q+n=0，所以q=-n，所以r=L。所以这个算法可以得到任意的线性变换。□

Eucild算法

定理：gcd（A，B）=gcd（rem（B，A），A）（rem（B，A）指B和A的余数）。该定理用于求最大公约数。
定理：A和B的最大公约数同时也是A和B的最小正数线性变换。
请添加图片描述
我是霜_哀，在算法之路上努力前行的一位萌新，感谢你的阅读！如果觉得好的话，可以关注一下，我会在将来带来更多更全面的知识讲解！