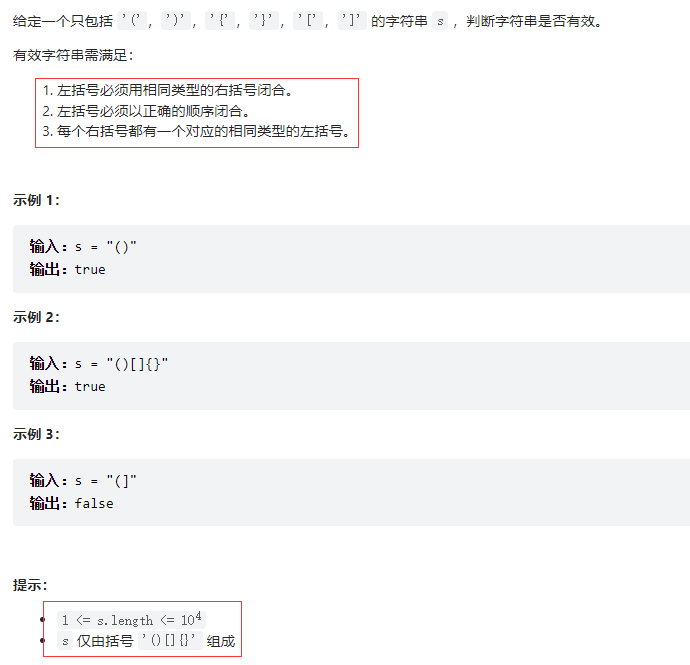
题目描述

思路

1.判断括号的有效性可以使用「栈」这一数据结构来解决
2.遍历给定的字符串 s。当遇到一个左括号时，我们会期望在后续的遍历中，有一个相同类型的右括号将其闭合。由于后遇到的左括号要先闭合，因此我们可以将这个左括号放入栈顶。
3.当我们遇到一个右括号时，我们需要将一个相同类型的左括号闭合。此时，我们可以取出栈顶的左括号并判断它们是否是相同类型的括号。如果不是相同的类型，或者栈中并没有左括号，那么字符串 s 无效，返回 False。为了快速判断括号的类型，我们可以使用哈希表存储每一种括号。哈希表的键为右括号，值为相同类型的左括号。
4.在遍历结束后，如果栈中没有左括号，说明我们将字符串 s 中的所有左括号闭合，返回 True，否则返回 False。
5.注意到有效字符串的长度一定为偶数，因此如果字符串的长度为奇数，我们可以直接返回 False，省去后续的遍历判断过程。

#include<iostream>
#include<string>
#include<unordered_map>
#include<stack>

using namespace std;

bool isValid(string s){
		int len = s.size();
		if(len%2 !=0){
			return false;
		}
		unordered_map <char, char> pairs{{')', '('}, {']', '['}, {'}', '{'}};
		stack<char> st;
		for (char ch: s){
			if(pairs.count(ch)){   //count找到则返回1，否则返回0 
				if(st.empty() || st.top()!=pairs[ch]){
					return false;
				}
				st.pop();
			}
			else{   //其他字符放到栈里面   如(())   
				st.push(ch);
			}
		}
		return st.empty();
} 

int main(){
	string str;
	getline(cin, str);
	bool res = isValid(str);
	cout<<res<<endl;
}

复杂度

• 时间复杂度O(n)，其中n是字符串s的长度
• 空间复杂度O(n+∣Σ∣)，其中 Σ 表示字符集，本题中字符串只包含 6 种括号，∣Σ∣=6。栈中的字符数量为 O(n)，而哈希表使用的空间为 O(∣Σ∣)，相加即可得到总空间复杂度

关于哈希表的find和count的使用

• 使用count，返回的是被查找元素的个数。如果有，返回1；否则，返回0。注意，map中不存在相同元素，所以返回值只能是1或0。
• 使用find，返回的是被查找元素的位置，没有则返回map.end()。