数据结构与算法基础（青岛大学-王卓）(4)

第四弹啊，栈和队列终于叮叮咚咚看完了，小龙虾呀鳝鱼汤啊倍儿香~~~~，配合本文食用更香 😃

文章目录

- - 栈和队列
  - - 栈
    - 队列
    - 案列的引入
    - 栈的表示和操作
    - - 栈的抽象数据类型定义
      - 顺序栈
      - 顺序栈的表示
        顺序栈的初始化
        顺序栈基本操作
        顺序栈的入栈
        顺序栈的出栈
      - 链栈
      - 链栈基本操作
    - 栈和递归
    - - 递归的定义
      - 递归问题一用**分治法**求解
      - 递归优缺点
    - 队列的表示和操作
    - - 队列的**抽象数据类型**定义
      - 循环队列(顺序表示)
      - 队列的真溢出和假溢出
        循环队列在队空和队满时的条件都为 front == rear, 如何分辨？
        循环队列的操作
      - 链队(链式表示)
      - 类型定义
        链队指针变化情况
        链队的基本操作

栈和队列

栈和队列是限定插入和删除只能在表的“端点”进行的线性表
- 他们都是线性表的子集(一种插入和删除受限的线性表)
栈的应用(后进后出)
队列的应用(先进先出)

栈

栈(stack)是仅在表尾进行插入，删除的线性表，又称为后进先出(Last In First Out)的线性表，简称LIFO结构。
表尾(an)称为栈顶Top, 表头(a1)称为栈底Base
入栈(PUSH)
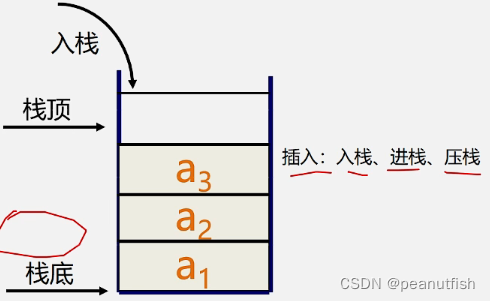
出栈(POP)
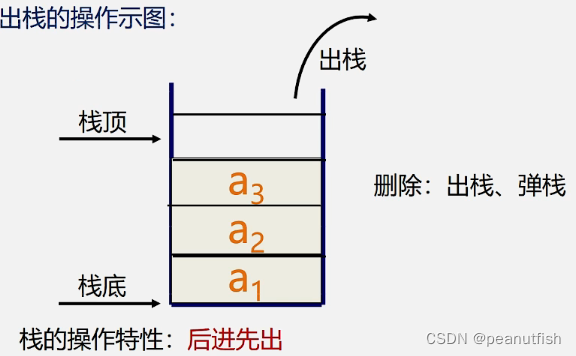
相关概念

队列

队列(queue)是一种先进先出(First In First Out) FIFO结构的线性表，表尾插入表头删除。
相关概念

案列的引入

进制转换 - “十进制整数N向其它进制数d(二，八，十六)的转换是计算机实现,该转换法则：除以d倒取余，对应于一个简单算法原理： n=(n div d)*d+n mod d （其中：div为整除运算，mod为求余运算)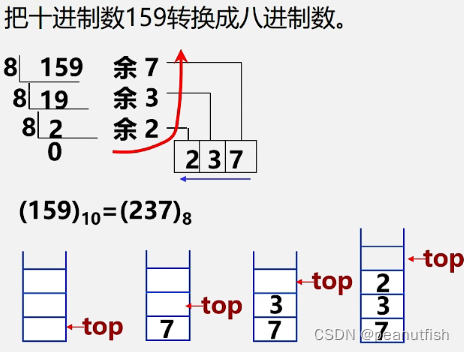
括号匹配的检验
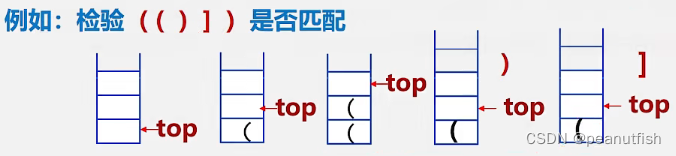
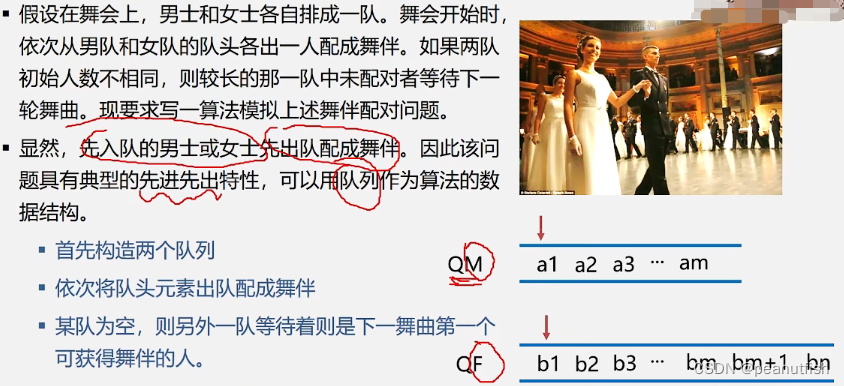
舞伴问题

栈的表示和操作

栈的抽象数据类型定义

ADT Stack{ 
    数据对象： D={ai|ai ∈ ElemSet,i=1,2...n，n>=0} 
    数据关系: R1={<ai-1,ai>|ai-1,ai∈D,i=2,...,n} 
    		约定an端为栈顶，a1端为栈底。 
    基本操作：初始化、进栈、出栈、取栈顶元素等 
}ADT Stack

在这里插入图片描述

顺序栈

存储方式，同一般线性表的顺序存储结构完全相同，利用一组地址连续的存储单元依次存放自栈底到栈顶的数据元素。栈底一般在低地址端。

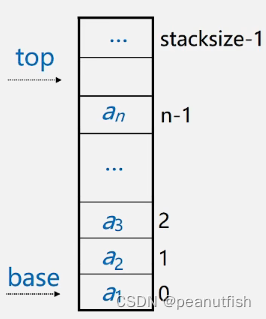
附设top指针，指示栈顶元素在顺序栈中的位置。
另设base指针，指示栈底元素在顺序栈中的位置。
但是，为了方便操作，通常top指示真正的栈顶元素之上的下标地址
另外，用stacksize表示栈可使用的最大容量

使用数组作为顺序栈的存储方式，优点简单方便，但是容易溢出，

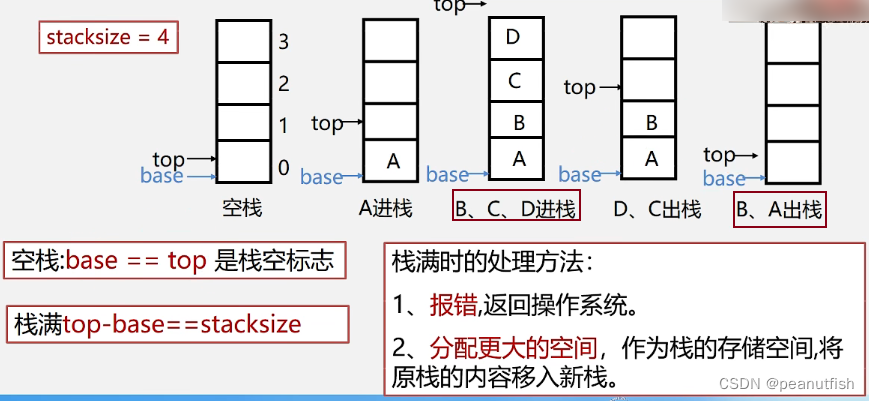
空栈和栈满判断条件如下，分别会产生下面的溢出
上溢(overflow): 栈已满还要压入元素 --> 属于错误，使问题无法进行
下溢(underflow): 栈已空还要弹出元素 --> 看做结束条件

顺序栈的表示

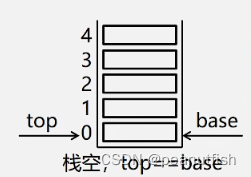
#define MAXSIZE 100
typedef struct{
	SElemType *base; / / 栈底指针
	SElemType *top; / / 栈顶指针
	int stacksize; / / 栈可用最大容量
}SqStack;

顺序栈的初始化

在这里插入图片描述

Status InitStack(SqStack &S) { //构造一个空栈
    S.base = new SElemType[MAXSIZE]; //c++
    S.base = (SElemType*)malloc(MAXSIZE*sizeof(SElemType)); // 或者c
    if(!S.base) exit(OVERFLOW); //存储分配失败时处理
    S.top = S.base; // 栈顶指针等于栈底指针
    S.stacksize = MAXSIZE;
    return OK;
}

顺序栈基本操作

// 顺序栈判断栈是否为空
Status StackEmpty(SqStack S){
    // 为空返回True
    if (S.top == S.base)
        return True;
    else
        return False;
}

// 顺序栈的长度
int StackLength(SqStack S) {
    return S.top - S.base;
}

// 清空顺序栈
Status ClearStack(SqStack S){
    if(S.base) S.top = S.base; // 清空不需要动数据，直接动top指针
    return OK;
}

// 销毁顺序栈
Staus DestroyStack(SqStack &S){
    if (S.base) {
        delete S.base; // 这里代表释放S.base指针空间，并没有删除，变成了野指针，所以后面需要赋NULL值
        S.stacksize=0;
        S.top = S.base = NULL;
    }
    return OK;
}

顺序栈的入栈

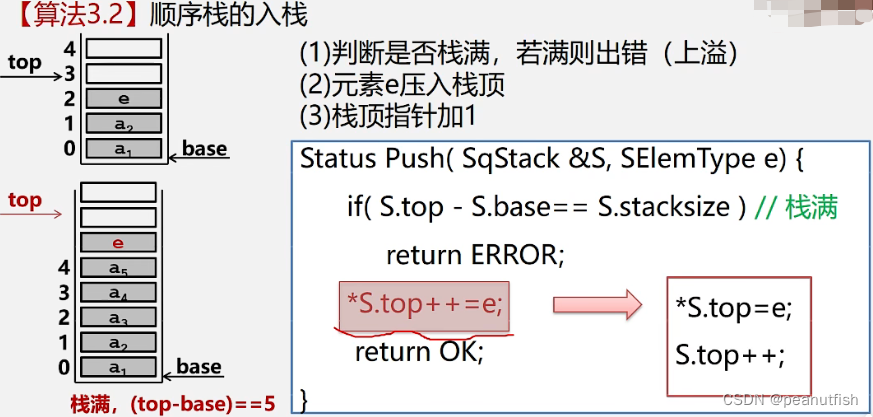
在这里插入图片描述

顺序栈的出栈

链栈

链栈是运算受限的单链表，只能在链表头部进行操作

链栈的表示

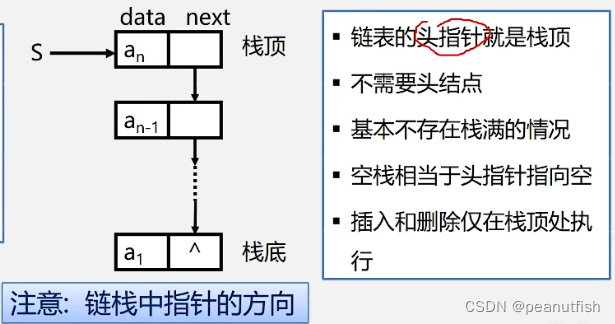
在这里插入图片描述

typede struct StackNode{
    SElemType data;
    struct StackNode *next;
} StackNode, *LinkStack;
LinkStack S;

链栈基本操作

// 链栈初始化
Void InitStack(LinkStack &S){
    S=NULL; // 构造一个空栈，栈顶指针为空
    return OK;
}

// 判断链栈为空
Status StackEmpty(LinkStack &S){
    if (S==NULL) return True;
    else retur False;
}

// 取栈顶元素
SElemType GetTop(LinkStack S){
    if (S!=NULL) return S->data;
}

// 链栈的入栈
Status PushStack(LinkStack &S, SElemType e){
    p = new StackNode; // 创建一个新的要插入的节点
    p.data = e; // data赋值
    p.next = S; // 新节点指向栈顶
    S = p; // 修改栈顶指针
    return OK；
}

// 链栈的出栈
Status PopStack(LinkStack &S, SElemType &e){
    if (S==NULL) return ERROR;
    e=S->data; // 删除的元素给e
    p=S; 
    S=S->next; // 栈顶指针下移
    delete p; //删除原来的栈顶指针
    return OK;
}

栈和递归

递归的定义

若一个对象部分地包含它自己，或用它自己给自己定义，则称这个对象是递归的；
若一个过程直接地或间接地调用自己则称这个过程是递归的过程。例如：递归求 n 的阶乘
以下三种情况常常用到递归方法
- 递归定义的数学函数
- 具有递归特性的数据结构
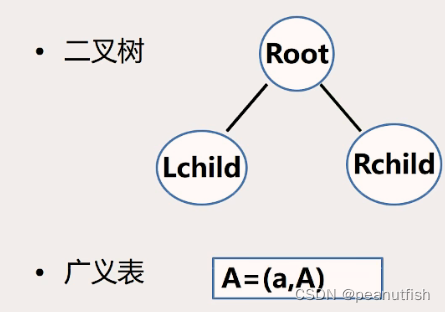
- 可递归求解的问题

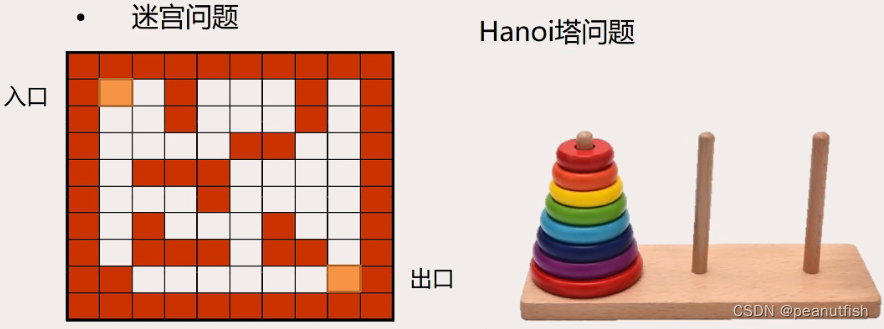
递归问题一用分治法求解

分治法：对于一个较为复杂的问题，能够分解成几个相对简单的且解法相同或类似的子问题来求解

必备的三个条件
- 能将一个问题转变成一个新问题，而新问题与原问题的解法相同或者类同、不同的仅是处理的对象，且这些处理对象是变化有规律的
- 可以通过上述转化而使问题简化
- 必须有一个明确的递归出口，或称递归的边界

分治法的形式

void p(参数表) {
    if (递归结束条件) 可直接求解步骤；--基本项
	else P(较小的参数); --归纳项
}

Example:

long Fact(long n){
    if (n==0) return 1;  //基本项
    else return n*Fact(n-1); //归纳项
}

在这里插入图片描述

递归优缺点

优点：结构清晰,程序易读

缺点：每次调用要生成工作记录，保存状态信息，入栈；返回时要出栈，恢复状态信息。时间开销大。

解决办法：

递归==>非递归

方法1：尾递归、单向递归 ==> 循环结构

在这里插入图片描述

方法2：自用栈模拟系统的运行时栈

在这里插入图片描述

队列的表示和操作

队列的抽象数据类型定义

ADT Queue{
	数据对象 ：D = { ai|ai属于ElemSet，i=1,2...n,n>=0}
	数据关系 ：R = {<ai-1，ai>|ai-1,ai属于D,i=1,2...,n} 约定其中 a1 端为队列头，an 端为队列尾 。
	基本操作 :
		lnitQueue(&Q)   操作结果 ： 构造空队列 Q
		DestroyQueue(&Q) 条件 ： 队列 Q 已存在 操作结果 ： 队列 Q 被销毁
		ClearQueue(&Q) 条件 ： 队列 Q 已存在  操作结果:将 Q 清空
		QueueLength(Q) 条件 ： 队列 Q 已存在 操作结果 ： 返回 0 的元素个数 ， 即队长
		GetHead(Q (e) 条件 ： Q 为非空队列 操作结果 ： 用 e 返回 Q 的队头元素
		EnQueue()Q e) 条件 ： 队列 Q 已存在 操作结果 ： 插入元素 e 为 Q 的队尾元素
		DeQueue()Q (e) 条件 ： Q 为非空队列 操作结果 ： 删除 Q 的队头元素 ， 用 e 返回值
        ...还有将队列置空 、 遍历队列等操作...
} ADT Queue

循环队列(顺序表示)

一维数组base[MAXQSIZE]

#define MAXQSIZE 100 // 最大队列长度
Typedef struct {
    QElemType *base; // 初始化动态分配存储空间(指向数组首元素的指针)
    int front; // 头指针
    int rear; // 尾指针
}SqQueue;

队列的真溢出和假溢出

在这里插入图片描述

解决假溢出问题 – 引入循环队列

实现方法：利用模(mod，C语言中：％）运算

插入元素: Q.base[Q.rear] = x;
Q.rear=(Q.rear+1)%MAXQSIZE;

删除元素: x=Q.base[s.front];
Q.front=(Q.front+1）%MAXQSIZE;

每当front/rear指针移动到最后位置的时候，通过模运算使其回到0，形成一个循环队列，可以循环使用为队列分配的存储空间。

循环队列在队空和队满时的条件都为 front == rear, 如何分辨？
- 另设一个标志来区别队空队满
- 另设一个变量，记录元素个数
- 少用一个元素空间（常用）队满：(rear+1)%MAXQSIZE==front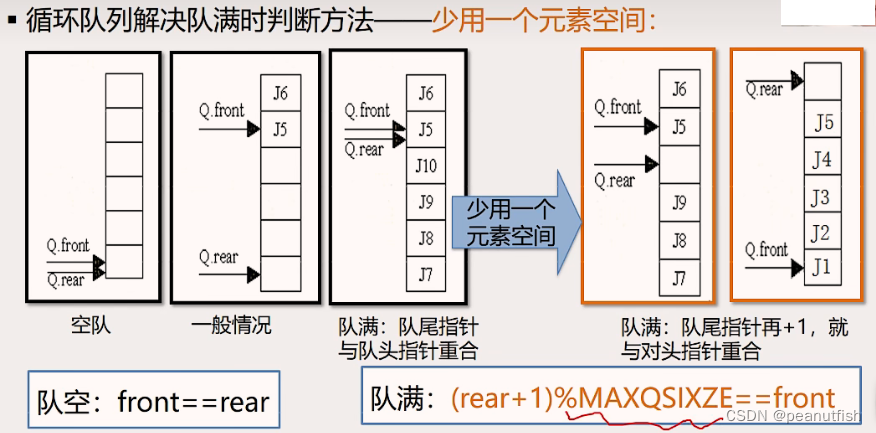

循环队列的操作

// 队列的初始化
Status InitQueue(SqQueue &Q){
    Q.base=new QElemType[MAXQSIZE]; //分配数组空间
    // Q.base=(QElemType*)malloc(MAXQSIZE*sizeof(QElemType));
    if(!Q.base) exit(OVERFLOW); //存储分配失败
    Q.front=Q.rear=0; //头尾指针为0，队列为空
    return OK;
}

// 求队列的长度
int QueueLength(SqQueue Q){
    return (Q.rear-Q.front+MAXQSIZE)%MAXQSZIE; // 需要考虑Q.rear比Q.front小的情况
}

// 循环队列入队
Status EnQueue(SqQueue &Q, QElemType e){
    if (Q.rear+1)%MAXQSIZE==Q.front return ERROR; // 判断是否队满
    Q.base[Q.rear]=e;
    Q.rear=(Q.rear+1)%MAXQSIZE;
    return OK;
}

// 循环队列的出队
Status DeQueue(SqQueue &Q, QElemType &e){
    if (Q.read==Q.front) return ERROR; 判断是否队空
    e=Q.base[Q.front];
    Q.front=(Q.front+1)%MAXQSIZE;
}

// 取队头元素
QElemType GetHead(SqQueue Q){
    if (Q.front!=Q.rear)
        return Q.base[Q.front];
}

链队(链式表示)

类型定义

#define MAXQSIZE 100  // 最大队列长度
typedef struct Qnode {
	QElemType data;
	struct Qnode *next;
}QNode, *QueuePtr;


typedef struct LinkQueue{
    QueuePtr front; // 队头指针
    QueuePtr rear; // 队尾指针
}LinkQueue;

链队指针变化情况

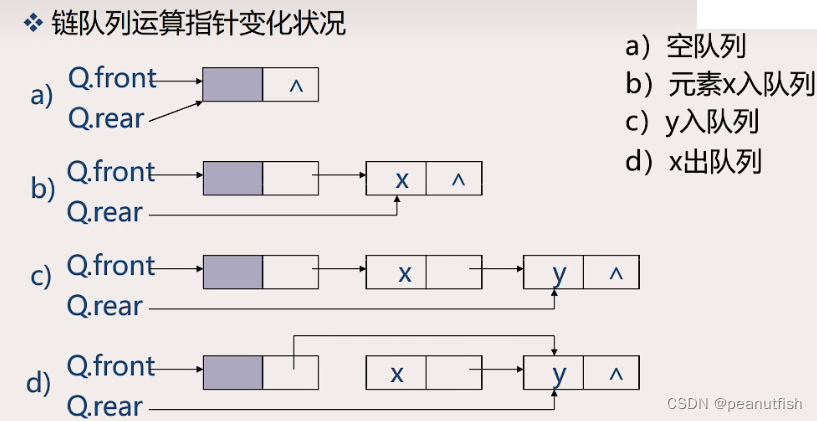
在这里插入图片描述

链队的基本操作

// 链队列的初始化
Status InitQueue(LinkQueue &Q){
    Q.front=Q.rear=(QueuePtr)malloc(sizeof(Qnode));
    if(!Q.front) exit(OVERFLOW);
    Q.front->next=NULL;
    return OK;
}

//链队列的销毁(从头结点开始，依次释放所有节点)
Status DestroyQueue(LinkQueue &Q){
    While(Q.front){
        p=Q.front->next; free(Q.front); Q.front=p; // 使用临时指针p
        // Q.rear=Q.front->next; free(Q.front);Q.front=Q.rear; 使用没有存在感的rear指针，闲着也是闲着
    }
    return OK;
}

// 链队列的入队
Status EnQueue(LinkQueue &Q, QElemType e){
    p=(QueuePtr)malloc(sizeof(QNode)); //分配新节点
    if(!p) exit(OVERFLOW); // 好习惯判断是否分配失败
    p->data=e; p->next=NULL; // 新节点赋值，next置空
    Q.rear->next=p; // 原尾结点指向新节点 
    Q.rear=p; //尾指针移动
    return OK;
}

// 链队列的出队
Status DeQueue(LinkQueue &Q, QElemType &e){
    if (Q.front == Q.rear) return ERROR;
    e=Q.front->data;
    p=Q.front->next; // 临时指针p
    Q.front->next=p->next; // 头指针指向下下一个节点
    if (Q.rear==p) Q.rear=Q.front; // 如果删除的节点刚好是尾结点，那么删除后尾指针也需要指向头结点，不然就孤家寡人了
    delete p;
    return OK;
}

// 求链队的队头元素
Status GetHead(LinkQueue Q, QElemType &e){
    if (Q.front==Q.rear) return ERROR;
    return Q.front->next->data;
    return OK;
}

TO BE CONTINUED…