接上次博客：初阶数据结构（6）（队列的概念、常用的队列方法、队列模拟实现【用双向链表实现、用数组实现】、双端队列 (Deque)、OJ练习【用队列实现栈、用栈实现队列】）_di-Dora的博客-CSDN博客

目录

树形结构的概念

一些重要概念：

树的表示形式

树的应用

二叉树

 两种特殊的二叉树

二叉树的性质

二叉树的存储

二叉树的遍历

1. 前中后序遍历

2. 层序遍历

二叉树的基本操作

二叉树相关的 OJ 题

1. 检查两颗树是否相同

2. 另一颗树的子树

3. 翻转二叉树

4. 判断一颗二叉树是否是平衡二叉树

5. 对称二叉树

6. 二叉树的构建及遍历

7. 二叉树的分层遍历

8. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先

9. 根据一棵树的前序遍历与中序遍历构造二叉树

10. 根据一棵树的中序遍历与后序遍历构造二叉树

11. 二叉树创建字符串

12. 二叉树前序非递归遍历实现

13. 二叉树中序非递归遍历实现

 14. 二叉树后序非递归遍历实现

---

树形结构的概念

 树是一种非线性的数据结构，它是由n（n>=0）个有限结点组成一个具有层次关系的集合，这些结点之间通过边连接。树具有层次关系，它的形状类似于一棵倒挂的树，根节点位于顶部，叶节点位于底部。

树的定义包括以下要点：

1. 根节点（Root）：树中的一个特殊节点，它没有前驱节点，是整个树的起点。
2. 子树（Subtree）：除根节点外，树中的每个节点都可以看作是一棵子树的根节点。子树是一棵与原树类似的树，它包含了一部分原树中的节点和边。
3. 前驱节点（Parent）和后继节点（Children）：一个节点的前驱节点是其所在子树的根节点，而该节点称为前驱节点的后继节点。每个节点可以有零个或多个后继节点。
4. 叶节点（Leaf）：没有后继节点的节点称为叶节点，也称为终端节点。叶节点位于树的底部，它们没有子树。

注意：

• 树的结构是递归定义的，每个节点都可以看作是一个根节点，包含了一棵子树。
• 树形结构中，子树之间不能有交集，即子树是不相交的，否则就不是树形结构
• 除了根节点外，每个结点有且仅有一个父节点；
• 一棵N个结点的树，有N-1条边。

一些重要概念：

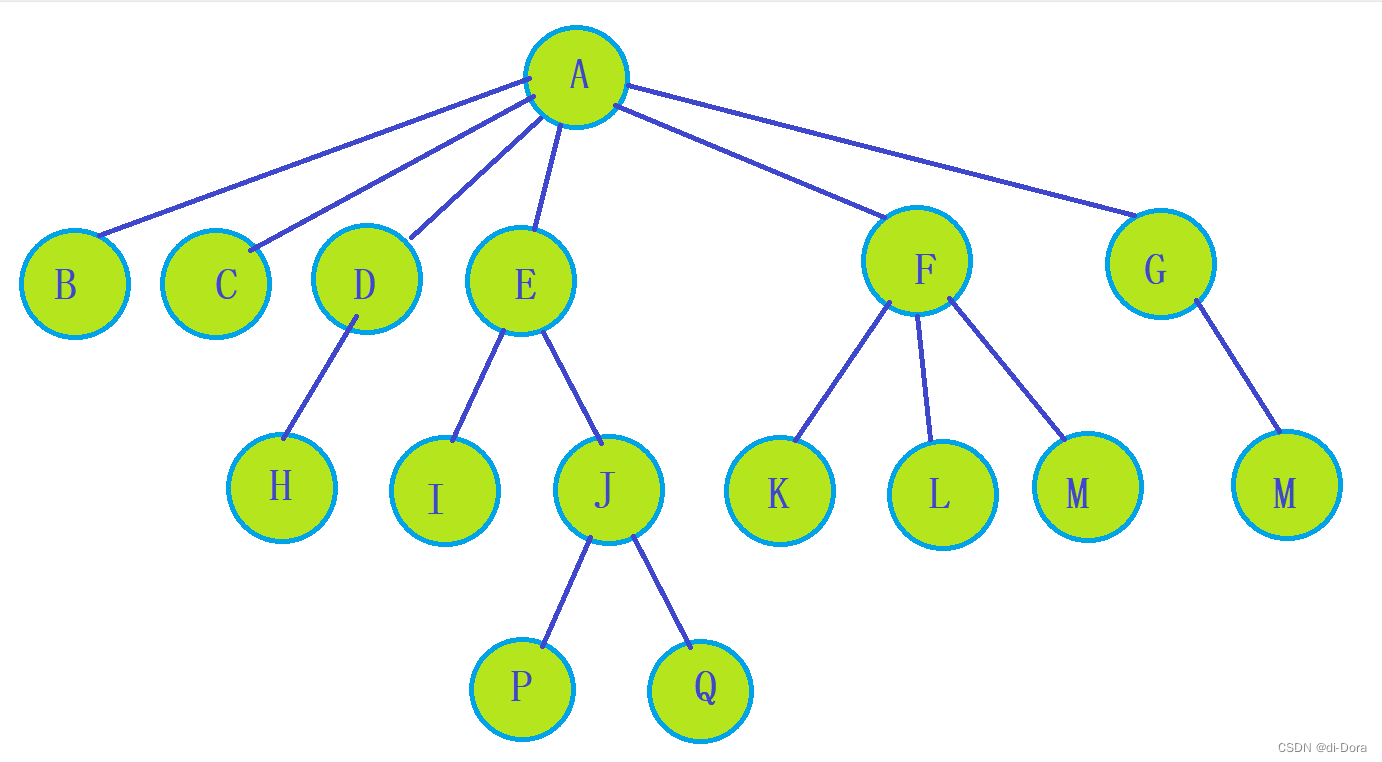
• 结点的度：一个结点含有子树的个数称为该结点的度； 如上图：A的度为6 ；
• 树的度：一棵树中，所有结点度的最大值称为树的度； 如上图：树的度为6；
• 叶子结点或终端结点：度为0的结点称为叶结点； 如上图：B、C、H、I...等节点为叶结点；
• 双亲结点或父结点：若一个结点含有子结点，则这个结点称为其子结点的父结点； 如上图：A是B的父结点；
• 孩子结点或子结点：一个结点含有的子树的根结点称为该结点的子结点； 如上图：B是A的孩子结点；
• 根结点：一棵树中，没有双亲结点的结点；如上图：A；
• 结点的层次：从根开始定义起，根为第1层，根的子结点为第2层，以此类推；
• 树的高度或深度：高度是树中结点的最大层次； 如上图：树的高度为4；深度是针对某一个结点而言的，最大的深度是树的高度；根节点的深度为1表示它是树中最顶层的节点，位于树的第一层。深度是用来描述节点在树中所处的层次位置，根节点的深度为1，它的子节点深度为2，依次类推。深度的概念用于描述节点之间的垂直关系，帮助我们理解树的结构和节点之间的层次关系。

树的以下概念只需了解，在看书时只要知道是什么意思即可：

• 非终端结点或分支结点：度不为0的结点； 如上图：D、E、F、G...等节点为分支结点；
• 兄弟结点：具有相同父结点的结点互称为兄弟结点； 如上图：B、C是兄弟结点；
• 堂兄弟结点：双亲在同一层的结点互为堂兄弟；如上图：H、I互为堂兄弟结点；
• 结点的祖先：从根到该结点所经分支上的所有结点；如上图：A是所有结点的祖先；
•  子孙：以某结点为根的子树中任一结点都称为该结点的子孙。如上图：所有结点都是A的子孙；
• 森林：由m（m>=0）棵互不相交的树组成的集合称为森林。

树的表示形式

树结构相对线性表就比较复杂了，要存储表示起来就比较麻烦了，实际中树有很多种表示方式，如：双亲表示法， 孩子表示法、孩子双亲表示法、孩子兄弟表示法等等。我们这里就简单的了解其中最常用的孩子兄弟表示法。 

1、双亲表示法（Parent Representation）：

class TreeNode {
    int data;
    int parentIndex;
}

class ParentTree {
    TreeNode[] nodes;
}

在双亲表示法中，每个节点包含一个指向其父节点的索引。整个树的节点以数组的形式存储，通过索引关系连接节点。

2、孩子表示法（Child Representation）：

class TreeNode {
    int data;
    List<TreeNode> children;
}

 在孩子表示法中，每个节点包含一个指向其子节点的列表。树的结构通过节点之间的引用关系来表示。

3、孩子双亲表示法（Child-Parent Representation）：

class TreeNode {
    int data;
    TreeNode parent;
    List<TreeNode> children;
}

在孩子双亲表示法中，每个节点除了包含指向其子节点的列表外，还包含一个指向其父节点的引用。

4、孩子兄弟表示法（Child-Sibling Representation）：

class TreeNode {
    int data;// 树中存储的数据
    TreeNode parent;
    TreeNode firstChild;// 第一个孩子引用
    TreeNode nextSibling;// 下一个兄弟引用
}

 在孩子兄弟表示法中，每个节点包含指向其第一个子节点和下一个兄弟节点的引用。

树的应用

树的常见应用包括文件系统的表示、数据库索引、组织结构等。

树型结构的特点使得它在表示具有层次关系的数据时非常有用。它提供了一种清晰且灵活的方式来组织和管理数据。树结构的算法和操作通常基于递归的思想，它们可以用来解决许多问题，如搜索、排序、遍历等。树是计算机科学中重要的基础数据结构之一。

二叉树

二叉树是一种特殊的树结构，其中每个节点最多有两个子节点：一个称为左子节点，另一个称为右子节点。

二叉树的定义具有以下特点：

二叉树可以是空的（没有节点），也可以由一个根节点加上左子树和右子树组成。

每个节点最多有两个子节点，即左子节点和右子节点。这意味着每个节点最多可以有两个分支。

左子树和右子树都是二叉树，它们也可以为空。

二叉树的子树之间是相互独立的，即左子树和右子树互不影响。

二叉树的形状可以多样化，它可以是平衡的或不平衡的，可以是满二叉树（每个节点都有两个子节点）或完全二叉树（除了最后一层外，其他层的节点都是满的）。

二叉树在计算机科学中被广泛应用，包括二叉搜索树、堆、表达式树等。

在实现二叉树的代码中，一个二叉树节点通常包含一个值和指向左子节点和右子节点的引用。每个节点通过这些引用形成树的结构。通过递归或迭代的方式，可以对二叉树进行遍历、搜索、插入、删除等操作。二叉树的性质使得它在很多场景下都非常有用，例如在排序、搜索和表示层次结构等方面。

注意：

1. 二叉树不存在度大于2的结点

2. 二叉树的子树有左右之分，次序不能颠倒，因此二叉树是有序树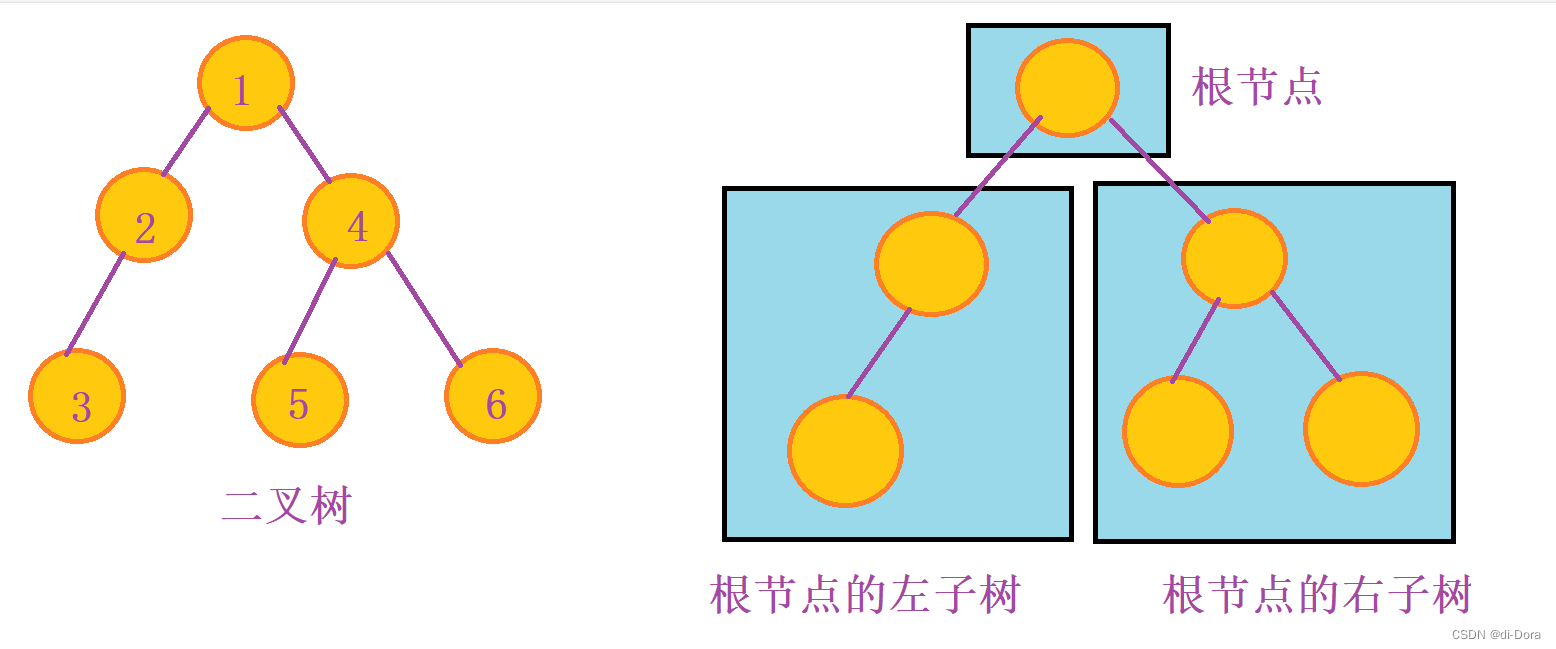

对于任意的二叉树都是由以下几种情况复合而成的：

 两种特殊的二叉树

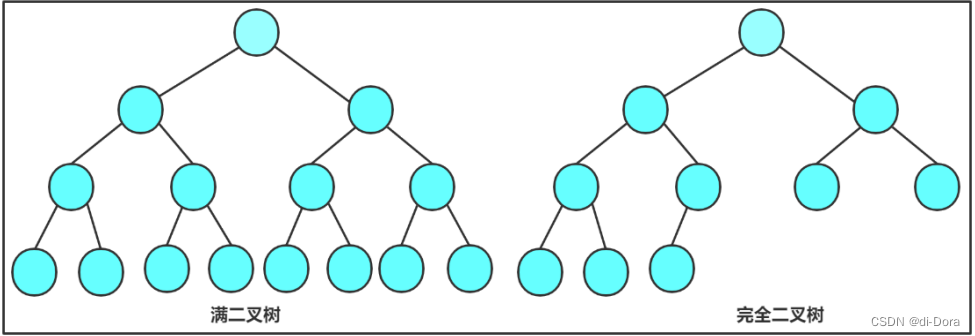
1. 满二叉树: 一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵二叉树的层数为K，且结点总数是 2 的 k次方 再 -1 (k>=0)，则它就是满二叉树。

2. 完全二叉树: 完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。即从上到下、从左到右依次存放，而不跳过某个结点。要注意的是满二叉树是一种特殊的完全二叉树。

二叉树的性质

1. 若规定根结点的层数为1，则一棵非空二叉树的第 i 层上最多（每个结点都存在两个左右孩子）有2 的（i - 1）次方 ( i > 0 )个结点；

2. 若规定只有根结点的二叉树的深度为1，则深度为K的二叉树的最大结点数是2 的 k次方 -1 (k>=0)；比如：深度为4的二叉树最多有15结点，2的4次方-1.

3. 对任何一棵二叉树, 如果其叶结点个数为 n0 , 度为2的非叶结点个数为 n2 ,则有 n0＝n2＋1 。即对于任何一棵二叉树，叶子结点的个数永远比度为2的结点的个数多1；怎么得到这个公式的？

对任何一棵二叉树, 如果其叶结点个数为 n0, 度为1的非叶结点个数为 n1 ,度为2的非叶结点个数为 n2 ,有：

表达式1：N=n0+n1+n2;

我们刚刚说过：一棵N个结点的树，有N-1条边，度为0的结点向下不会产生边，度为1的结点向下产生1条边，度为2的结点向下产生2条边，所以：

表达式2：N-1=n1 + 2*n2；

联立解得：n0＝n2＋1 。

4. 具有n个结点的完全二叉树的深度k为 log以2为底的(n+1)向上取整（或者 log以2为底的 (n)+1向下取整）；

5. 对于具有n个结点的完全二叉树，如果按照从上至下从左至右的顺序对所有节点从0开始编号，则对于序号为i 的结点有：

• 若i>0，双亲序号：( i - 1 ) / 2；
• i = 0，i为根结点编号，无双亲结点；
• 若2i+1<n，左孩子序号：2 i +1，否则无左孩子；
• 若2i+2<n，右孩子序号：2 i +2，否则无右孩子；

---

 了解了性质，我们就要开始做练习了：

1. 某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）

A 不存在这样的二叉树

B 200

C 198

D 199

答案：B

解析：对于任何一棵二叉树，叶子结点的个数永远比度为2的结点的个数多1

2.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）

A n

B n+1

C n-1

D n/2

答案：A

解析：对于有偶数个结点的完全二叉树来说：度为1的结点一共有1个。对于奇数个结点的完全二叉树来说，度为1的结点一个0个。这是偶数个结点的二叉树，假设度为0的结点个数为x，n0＝n2＋1 ，所以度为2的结点个数为x-1，所以2n=x+1+x-1，n=x。

3.一个具有767个节点的完全二叉树，其叶子节点个数为（ )

 A 383

B 384

C 385

D 386

答案：B

解析：这题和上面那题差不多，但是这是奇数个结点的二叉树，假设度为0的结点个数为x，n0＝n2＋1 ，所以度为2的结点个数为x-1，所以767=x+x-1，x=384。

4.一棵完全二叉树的节点数为531个，那么这棵树的高度为（ ）

A 11

B 10

C 8

D 12

解析：具有n个结点的完全二叉树的深度k为 log以2为底的(531+1)上取整，2的9次方是512<532；

2的10次方为1024。

5.一颗拥有1000个结点的树度为4，则它的最小深度是（ ）

A.5

B.6

C.7

D.8

答案：B

解析：如果这棵树每一层都是满的，则它的深度最小，所以它是一个四叉树，高度为N，则这个数的节点个数为(4^N - 1) / 3，这里运用的是等差数列求和，当h = 5, 最大节点数为341， 当h = 6, 最大节点数为1365，所以最小深度应该为6。

6.设根结点的深度为1，则一个拥有n个结点的二叉树的深度一定在（   ）区间内

A.[log(n + 1)，n]

B.[logn，n]

C.[log(n + 1)，n - 1]

D.[log(n + 1)，n + 1]

答案：A

解析：

最大深度： 即每次只有一个节点，次数二叉树的高度为n，为最高的高度。

最小深度： 此树为完全二叉树， 如果是完全二叉树，根据二叉树性质，完全二叉树的高低为 h = log以2为底(n+1)向上取整。

二叉树的存储

在学习二叉树的基本操作前，我们需先要创建一棵二叉树，然后才能学习其相关的基本操作。但是由于现在我们对二叉树结构掌握还不够深入，所以我么先手动快速创建一棵简单的二叉树，快速进入二叉树操作学习，等二叉树结构了解的差不多时，我们反过头再来研究二叉树真正的创建方式。

二叉树的存储结构分为：顺序存储和类似于链表的链式存储。

我们先来看看第二种， 二叉树的链式存储是通过一个一个的节点引用起来的，常见的表示方式有二叉和三叉表示方式，具体如下：

// 孩子表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
}

// 孩子双亲表示法
class Node {
int val; // 数据域
Node left; // 左孩子的引用，常常代表左孩子为根的整棵左子树
Node right; // 右孩子的引用，常常代表右孩子为根的整棵右子树
Node parent; // 当前节点的根节点
}

public class BinaryTree {
    public static class BTNode{
        BTNode left;
        BTNode right;
        int value;
        BTNode(int value){
            this.value = value;
        }
    }

    private BTNode root;// 将来这个引用指向的是根节点

    public BTNode createBinaryTree(){
        BTNode node1 = new BTNode(1);
        BTNode node2 = new BTNode(2);
        BTNode node3 = new BTNode(3);
        BTNode node4 = new BTNode(4);
        BTNode node5 = new BTNode(5);
        BTNode node6 = new BTNode(6);
        root = node1;
        node1.left = node2;
        node2.left = node3;
        node1.right = node4;
        node4.left = node5;
        node5.right = node6;
        
        return node1; //这样甚至连头节点都不需要了
    }
}

public class Test {
    public static void main(String[] args) {
        BinaryTree binaryTree=new BinaryTree();
        BinaryTree.BTNode ret=binaryTree.createBinaryTree();
        System.out.println("-----------");
    }
}

二叉树的遍历

1. 前中后序遍历

学习二叉树结构，最简单的方式就是遍历。

所谓遍历(Traversal)，是指沿着某条搜索路线，依次对树中每个结 点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题(比如：打印节点内容、节点内容加 1)。 遍历是二叉树上最重要的操作之一，是二叉树上进行其它运算之基础。 

如果按照某种规则进行约定，则每个人对于同一棵树的遍历结果肯定是相同的。

如果N代表根节点，L代表根节点的 左子树，R代表根节点的右子树，则根据遍历根节点的先后次序有以下遍历方式：

• NLR：前序遍历(Preorder Traversal 亦称先序遍历)——访问根结点--->根的左子树--->根的右子树。
• LNR：中序遍历(Inorder Traversal)——根的左子树--->根节点--->根的右子树。
• LRN：后序遍历(Postorder Traversal)——根的左子树--->根的右子树--->根节点。 

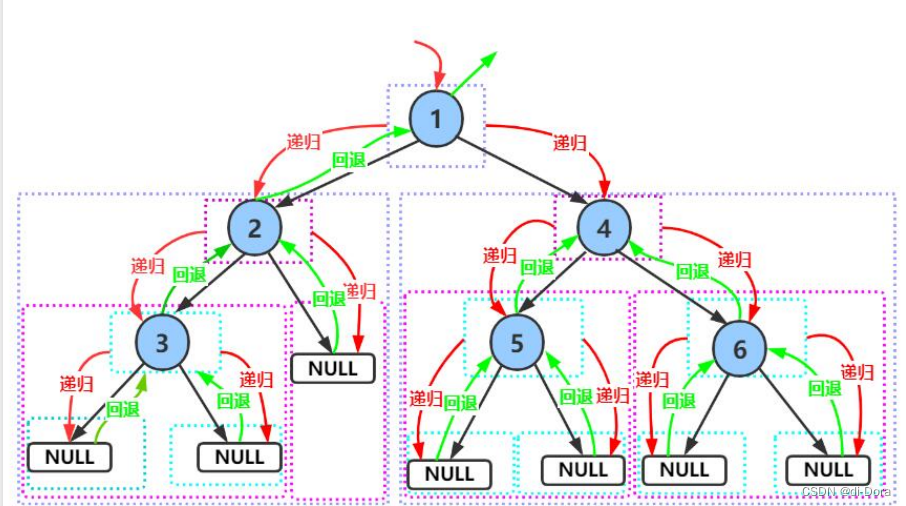
• 前序遍历结果：1 2 3 4 5 6
• 中序遍历结果：3 2 1 5 4 6
• 后序遍历结果：3 1 5 6 4 1

注意：对于每一个结点，都遵循同样的遍历方法。

再做一个简单的练习巩固一下： 

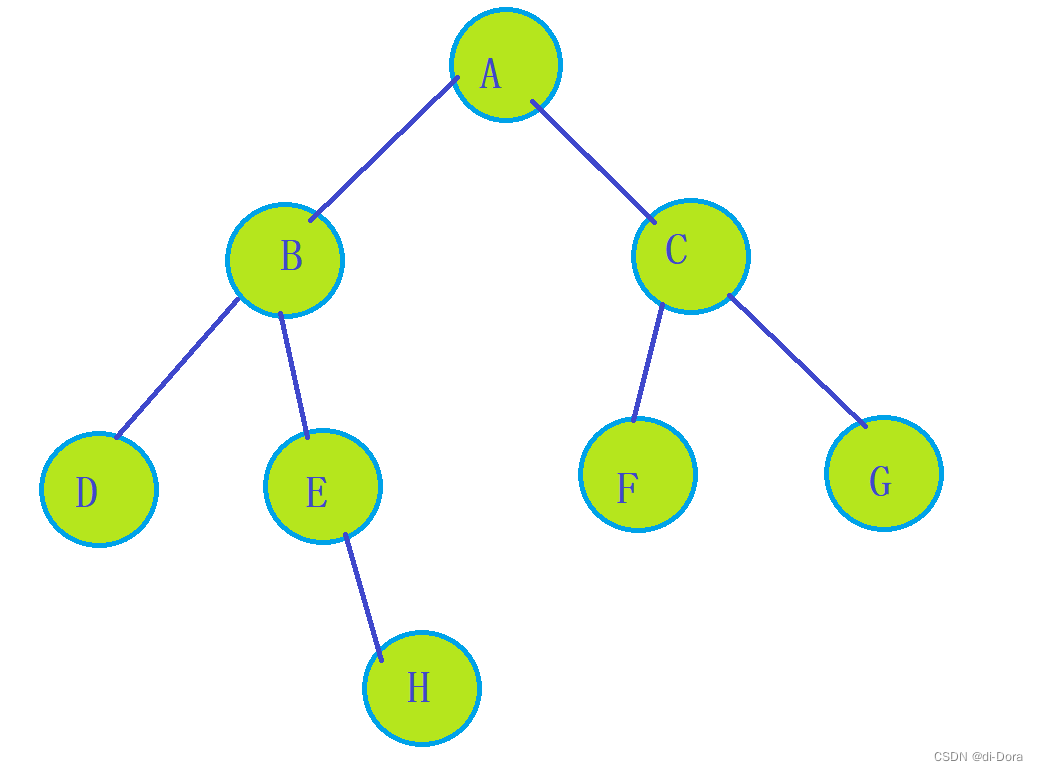
• 前序遍历结果：A B D E H C F G
• 中序遍历结果：D B E H A F C G
• 后序遍历结果：D H E B F G C A

 用代码遍历：

    public class BinaryTree {
        static class TreeNode {
            public char val;
            public TreeNode left;
            public TreeNode right;

            public TreeNode(char val) {
                this.val = val;
            }
        }


        public TreeNode createTree() {
            TreeNode A = new TreeNode('A');
            TreeNode B = new TreeNode('B');
            TreeNode C = new TreeNode('C');
            TreeNode D = new TreeNode('D');
            TreeNode E = new TreeNode('E');
            TreeNode F = new TreeNode('F');
            TreeNode G = new TreeNode('G');
            TreeNode H = new TreeNode('H');
            A.left = B;
            A.right = C;
            B.left = D;
            B.right = E;
            C.left = F;
            C.right = G;
            E.right = H;
            return A;
        }


        //递归的思想
        //前序遍历
        public void preOrder(TreeNode root){
            if(root==null) return;
            System.out.print(root.val+" ");
            preOrder(root.left);
            preOrder(root.right);
        }

        // 中序遍历
        public void inOrder(TreeNode root) {
            if (root == null) {
                return;
            }
            inOrder(root.left);
            System.out.print(root.val + " ");
            inOrder(root.right);
        }

        // 后序遍历
        public void postOrder(TreeNode root) {
            if (root == null) {
                return;
            }
            postOrder(root.left);
            postOrder(root.right);
            System.out.print(root.val + " ");
        }

    }

public class Test {
    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        BinaryTree.TreeNode ret = binaryTree.createTree();
        System.out.println("===");
        System.out.println("前序遍历");
        binaryTree.preOrder(binaryTree.createTree());
        System.out.println();
        System.out.println("中序遍历");
        binaryTree.inOrder(binaryTree.createTree());
        System.out.println();
        System.out.println("后序遍历");
        binaryTree.postOrder(binaryTree.createTree());
        System.out.println();
    }
}

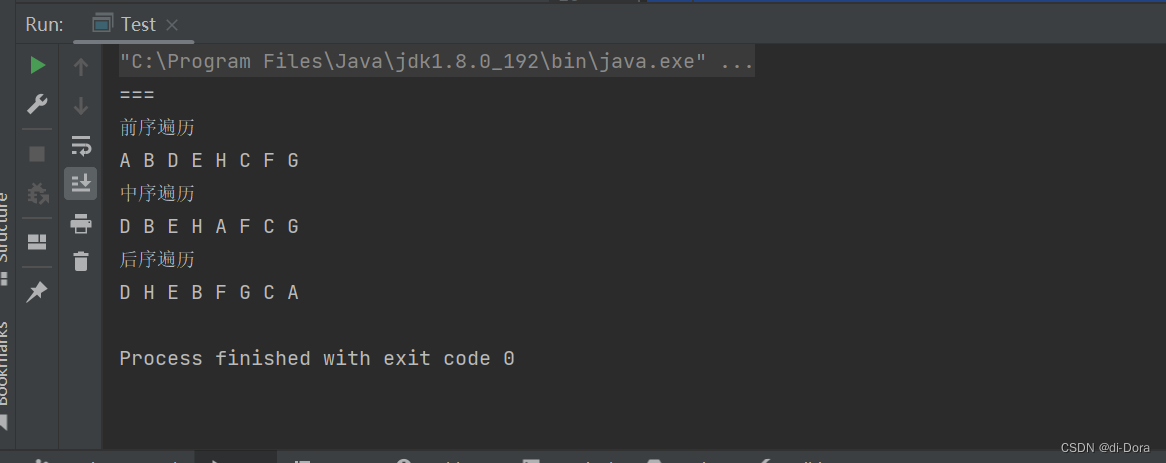 如果现在要求我们将前序遍历的结果不打印，而是存储到 List 中，怎么实现？

        public List<TreeNode> preOrder2(TreeNode root){
            List<TreeNode> list=new ArrayList<>();
            if(root==null) return list;
            list.add(root);

            List<TreeNode> leftTree=preOrder2(root.left);
            list.addAll(leftTree);

            List<TreeNode> rightTree=preOrder2(root.right);
            list.addAll(rightTree);

            return list;

        }
    public List<TreeNode> inOrder2(TreeNode root){
        List<TreeNode> list=new ArrayList<>();
        if(root==null) return list;

        List<TreeNode> leftTree=inOrder2(root.left);
        list.addAll(leftTree);

        list.add(root);

        List<TreeNode> rightTree=inOrder2(root.right);
        list.addAll(rightTree);
        return list;

    }
    public List<TreeNode> postOrder2(TreeNode root){
        List<TreeNode> list=new ArrayList<>();
        if(root==null) return list;

        List<TreeNode> leftTree=postOrder2(root.left);
        list.addAll(leftTree);

        List<TreeNode> rightTree=postOrder2(root.right);
        list.addAll(rightTree);

        list.add(root);
        return list;

    }



    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();
        BinaryTree.TreeNode ret = binaryTree.createTree();
        System.out.println("===");
        System.out.println("前序遍历");
        binaryTree.preOrder(binaryTree.createTree());
        System.out.println();
        System.out.println("中序遍历");
        binaryTree.inOrder(binaryTree.createTree());
        System.out.println();
        System.out.println("后序遍历");
        binaryTree.postOrder(binaryTree.createTree());
        System.out.println();
        System.out.println("=================================");
        List<BinaryTree.TreeNode> list =binaryTree.preOrder2(ret);
        for(BinaryTree.TreeNode tree:list){
            System.out.print(tree.val+" ");
        }
        System.out.println();
        System.out.println("=================================");
        List<BinaryTree.TreeNode> list2 =binaryTree.inOrder2(ret);
        for(BinaryTree.TreeNode tree:list2){
            System.out.print(tree.val+" ");
        }
        System.out.println();
        System.out.println("=================================");
        List<BinaryTree.TreeNode> list3 =binaryTree.postOrder2(ret);
        for(BinaryTree.TreeNode tree:list3){
            System.out.print(tree.val+" ");
        }
        System.out.println();

    }

2. 层序遍历

层序遍历：除了前序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在 层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层 上的节点，接着是第三层的节点，以此类推，即自上而下，自左至右逐层访问树的结点的过程就是层序遍历。

练习：

1.某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为()

A: ABDHECFG

B: ABCDEFGH

C: HDBEAFCG

D: HDEBFGCA

答案：A

2.二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为()

A: E

B: F

C: G

D: H

答案：A

解析：根节点就是先序遍历的第一个。如果加大难度，要画出图来，怎么画？

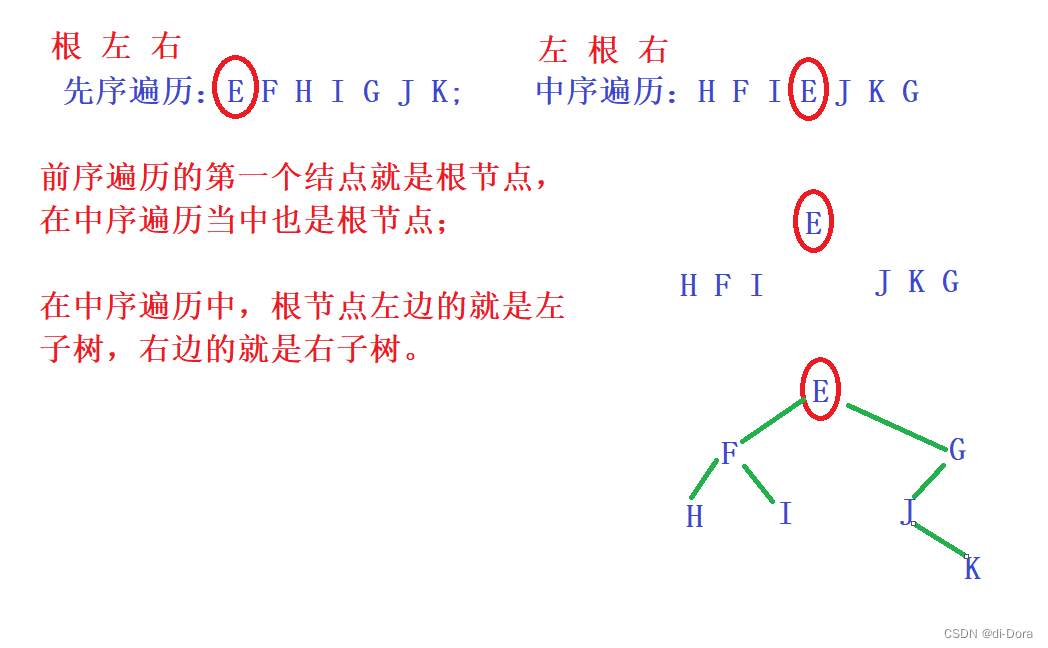
也就是说，我们一定要先通过前序遍历或者后序遍历找根节点，找到根节点之后，我们就去看中序遍历，以根节点为中心然后分左右子树。

分完左右子树后，我们再去看前序遍历或后序遍历的顺序：前者是根左右，后者是左右根。以本题前序遍历为例：

E后面的F就是根节点后面紧跟着的左子树的根。然后现在再回到中序遍历，以F为中心分F的左右子树。我们可以看到，H在F的左边，I在F的右边。

现在看右子树，E后面跳过已经确认过的 F、H、I ，就到了G。G就是根节点的右子树的根。然后现在回到中序遍历，以G为中心分G的左右子树。我们可以看到，J和K都在F的左边，回到前序遍历，发现J紧跟在G的后边，是G的左子树的根。回到中序遍历，K在J的右边，是J的右根。（可能有人会问，为什么K一定是J的右根，而不是G的右根？我们刚刚说过了，K与J都在G的左边，所以都归类于G的左子树。这就代表它们之间是不可能是兄弟节点。）

总之就是两个顺序反复确认，以此类推。

再来一题： 

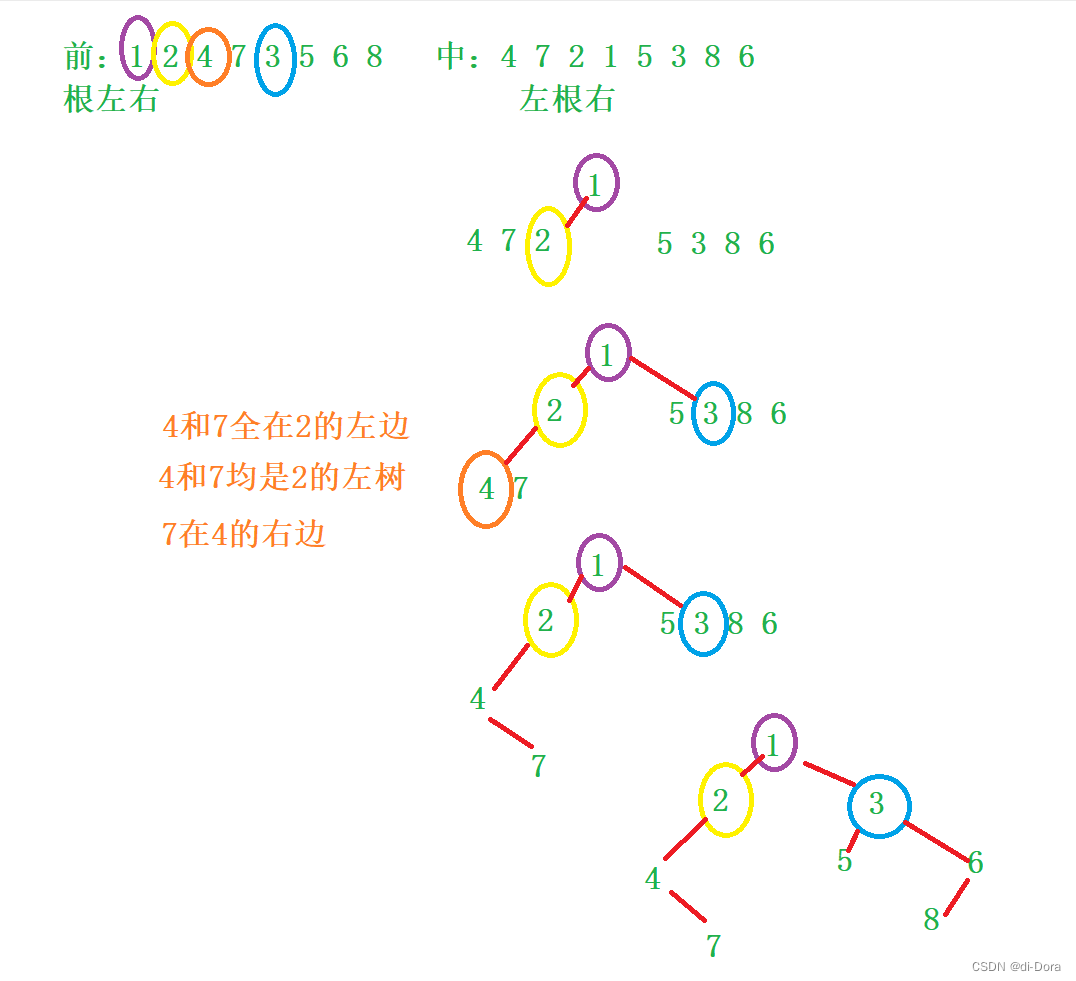
  3.设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为()

A: adbce

B: decab

C: debac

D: abcde

答案：D

解析：刚刚是前序和中序，现在是中序和后序。

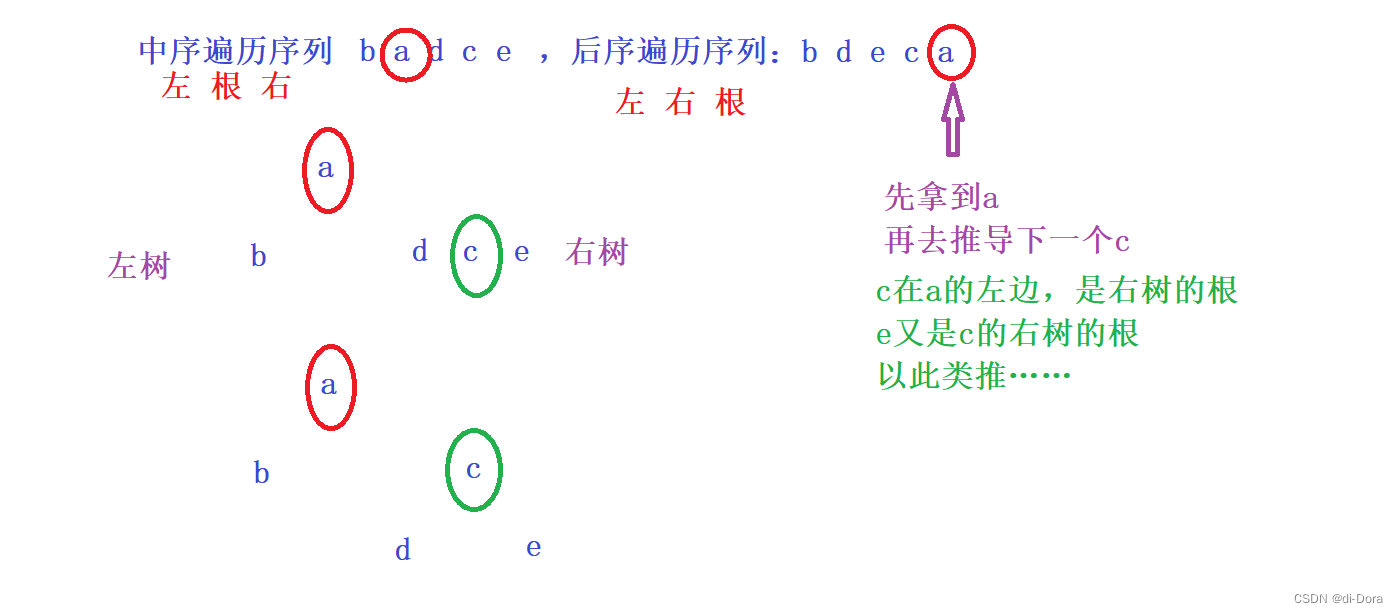
 那么，根据前序和后序，可以创建一个二叉树吗？

不可以！！！前序和后序只能确认根。没有中序就不可以确认左右。

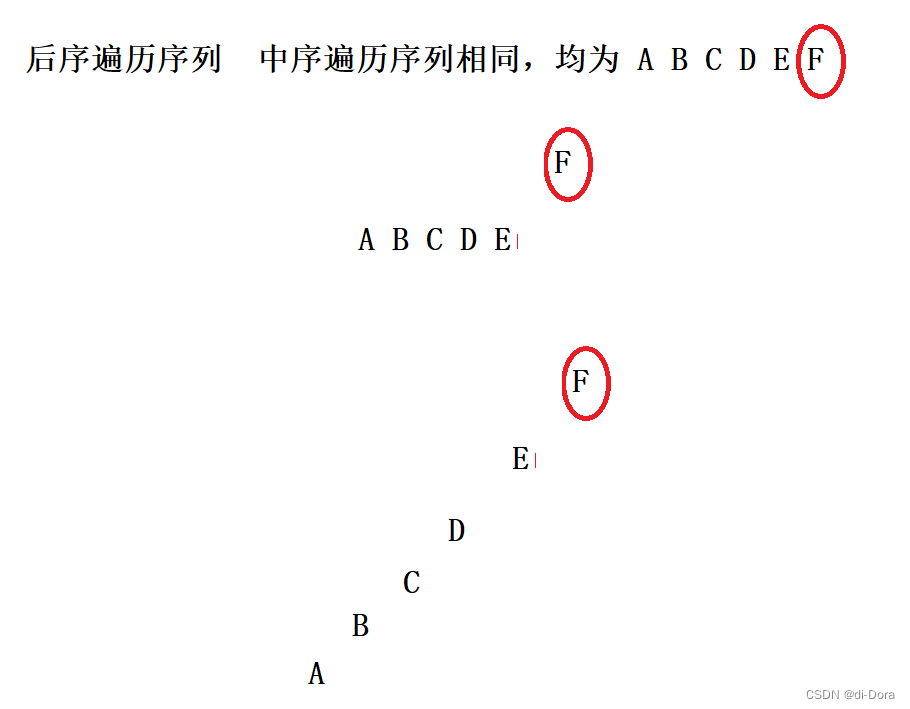
4.某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出(同一层从左到右)的序列为()

A: FEDCBA

B: CBAFED

C: DEFCBA

D: ABCDEF

答案：A

解析：只有左子树，没有右子树。

二叉树的基本操作

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

public class BinaryTree {
        static class TreeNode {
            public int val;
            public TreeNode left;
            public TreeNode right;

            public TreeNode(int val) {
                this.val = val;
            }
        }

        private TreeNode root;
        public TreeNode createTree() {
            TreeNode A = new TreeNode('A');
            TreeNode B = new TreeNode('B');
            TreeNode C = new TreeNode('C');
            TreeNode D = new TreeNode('D');
            TreeNode E = new TreeNode('E');
            TreeNode F = new TreeNode('F');
            TreeNode G = new TreeNode('G');
            TreeNode H = new TreeNode('H');
            A.left = B;
            A.right = C;
            B.left = D;
            B.right = E;
            C.left = F;
            C.right = G;
            E.right = H;
            return A;
        }

        public void preOrder(TreeNode root){
            if(root==null) return;
            System.out.print(root.val+" ");
            preOrder(root.left);
            preOrder(root.right);
        }
        // 中序遍历
        public void inOrder(TreeNode root) {
            if (root == null) {
                return;
            }
            inOrder(root.left);
            System.out.print(root.val + " ");
            inOrder(root.right);
        }

        // 后序遍历
        public void postOrder(TreeNode root) {
            if (root == null) {
                return;
            }
            postOrder(root.left);
            postOrder(root.right);
            System.out.print(root.val + " ");
        }

        public List<TreeNode> preOrder2(TreeNode root){
            List<TreeNode> list=new ArrayList<>();
            if(root==null) return list;
            list.add(root);

            List<TreeNode> leftTree=preOrder2(root.left);
            list.addAll(leftTree);

            List<TreeNode> rightTree=preOrder2(root.right);
            list.addAll(rightTree);

            return list;

        }
    public List<TreeNode> inOrder2(TreeNode root){
        List<TreeNode> list=new ArrayList<>();
        if(root==null) return list;

        List<TreeNode> leftTree=inOrder2(root.left);
        list.addAll(leftTree);

        list.add(root);

        List<TreeNode> rightTree=inOrder2(root.right);
        list.addAll(rightTree);
        return list;

    }
    public List<TreeNode> postOrder2(TreeNode root){
        List<TreeNode> list=new ArrayList<>();
        if(root==null) return list;

        List<TreeNode> leftTree=postOrder2(root.left);
        list.addAll(leftTree);

        List<TreeNode> rightTree=postOrder2(root.right);
        list.addAll(rightTree);

        list.add(root);
        return list;

    }

    // 获取树中节点的个数

    //以 前/中/后序 遍历这棵树的时候，会把每个节点都遍历到。遍历一个节点就计数一次
    //较笨拙的方法——遍历的思想
    public void size1(TreeNode root) {
        if (root == null) {
            return;
        }
        int size=0;
        size++;
        size1(root.left);
        size1(root.right);
    }
    //改进
    public int size2(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            return 1 + size2(root.left) + size2(root.right);
        }
    }



    // 获取叶子节点的个数
    //遍历的思想
    public void getLeafNodeCount1(TreeNode root) {
            int leafsize=0;
        if (root == null) {
            return ;
        }

        if (root.left == null && root.right == null) {
            leafsize++;
        }

        getLeafNodeCount1(root.left);
        getLeafNodeCount1(root.right);

    }

    //进阶  root左树的叶子+root右树的叶子=整棵树的叶子

    public int getLeafNodeCount2(TreeNode root) {
        if (root == null) {
            return 0;
        } else if (root.left == null && root.right == null) {
            return 1;
        } else {
            return getLeafNodeCount2(root.left) + getLeafNodeCount2(root.right);
        }
    }


    // 获取第K层节点的个数
    //root这棵树的第K层=root.left的第k-1层+root.right的第k-1层
    //以此类推直到k=1
    public int getKLevelNodeCount(TreeNode root, int k) {
        if (root == null || k < 1) {
            return 0;
        } else if (k == 1) {
            return 1;
        } else {
            return getKLevelNodeCount(root.left, k - 1) +
                    getKLevelNodeCount(root.right, k - 1);
        }
    }

    // 获取二叉树的高度
    public int getHeight(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = getHeight(root.left);
            int rightHeight = getHeight(root.right);
            return Math.max(leftHeight, rightHeight) + 1;
        }
    }
    public int getHeight2(TreeNode root) {
        if (root == null) {
            return 0;
        } else {
            int leftHeight = getHeight(root.left);
            int rightHeight = getHeight(root.right);
            return leftHeight > rightHeight ? leftHeight+ 1 : rightHeight+1;
        }
    }

    
    // 检测值为value的元素是否存在
    public TreeNode find(TreeNode root, int val) {
        if (root == null || root.val == val) {
            return root;
        } else {
            TreeNode leftResult = find(root.left, val);
            TreeNode rightResult = find(root.right, val);
            if (leftResult != null) {
                return leftResult;
            } else {
                return rightResult;
            }
        }
    }

    // 层序遍历
    public void levelOrder(TreeNode root) {
        if (root == null) {
            return;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();
            System.out.print(node.val + " ");

            if (node.left != null) {
                queue.offer(node.left);
            }

            if (node.right != null) {
                queue.offer(node.right);
            }
        }
    }

    // 判断一棵树是不是完全二叉树
    public boolean isCompleteTree(TreeNode root) {
        if (root == null) {
            return true;
        }

        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);

        boolean flag = false; // 标志位，用于判断是否遇到了非完全节点

        while (!queue.isEmpty()) {
            TreeNode node = queue.poll();

            if (node.left != null) {
                if (flag) {
                    return false; // 遇到非完全节点后，如果还有子节点，则不是完全二叉树
                }
                queue.offer(node.left);
            } else {
                flag = true; // 遇到了非完全节点
            }

            if (node.right != null) {
                if (flag) {
                    return false; // 遇到非完全节点后，如果还有子节点，则不是完全二叉树
                }
                queue.offer(node.right);
            } else {
                flag = true; // 遇到了非完全节点
            }
        }

        return true;
    }

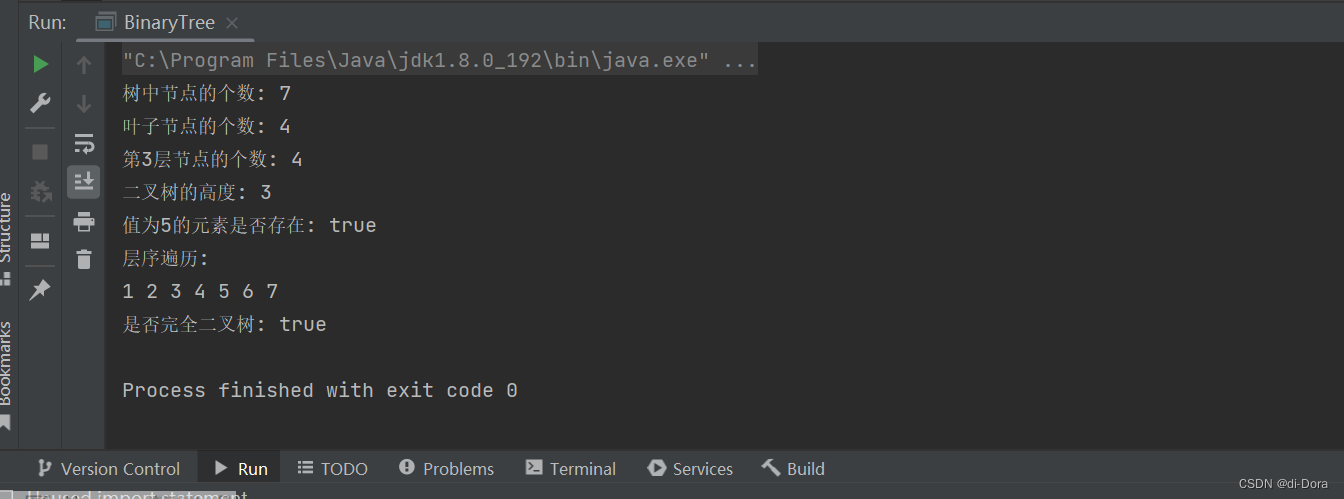
    public static void main(String[] args) {
        BinaryTree binaryTree = new BinaryTree();

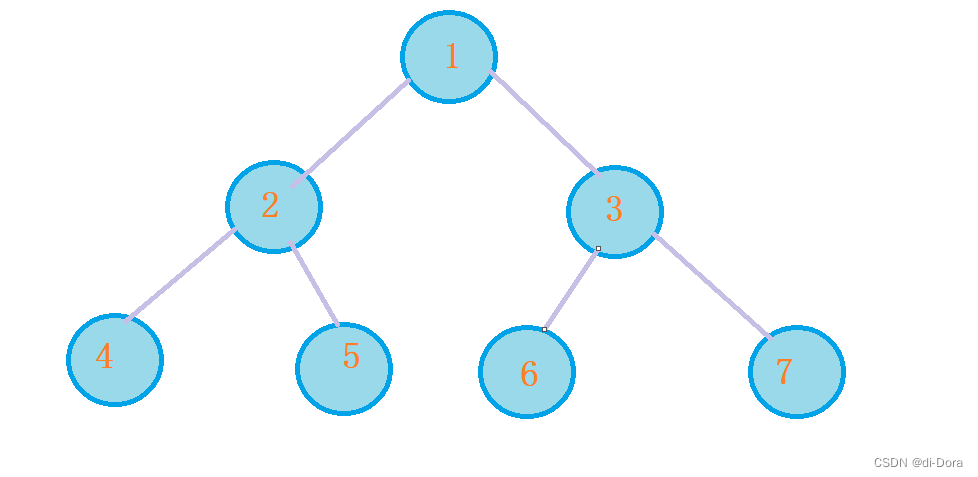
        // 构造二叉树
        binaryTree.root = new TreeNode(1);
        binaryTree.root.left = new TreeNode(2);
        binaryTree.root.right = new TreeNode(3);
        binaryTree.root.left.left = new TreeNode(4);
        binaryTree.root.left.right = new TreeNode(5);
        binaryTree.root.right.left = new TreeNode(6);
        binaryTree.root.right.right = new TreeNode(7);

        // 测试各个操作
        System.out.println("树中节点的个数: " + binaryTree.size2(binaryTree.root));
        System.out.println("叶子节点的个数: " + binaryTree.getLeafNodeCount2(binaryTree.root));
        System.out.println("第3层节点的个数: " + binaryTree.getKLevelNodeCount(binaryTree.root, 3));
        System.out.println("二叉树的高度: " + binaryTree.getHeight(binaryTree.root));
        System.out.println("值为5的元素是否存在: " + (binaryTree.find(binaryTree.root, 5) != null));
        System.out.println("层序遍历: ");
        binaryTree.levelOrder(binaryTree.root);
        System.out.println("\n是否完全二叉树: " + binaryTree.isCompleteTree(binaryTree.root));
    }
}

二叉树相关的 OJ 题

1. 检查两颗树是否相同

给你两棵二叉树的根节点 p 和 q ，编写一个函数来检验这两棵树是否相同。
如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

力扣：100. 相同的树 - 力扣（Leetcode）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSameTree(TreeNode p, TreeNode q) {
        // 如果两个树都为空，它们相同
        if (p == null && q == null) {
            return true;
        }
        // 如果只有一个树为空，它们不相同
        if (p == null || q == null) {
            return false;
        }
        // 如果根节点的值不相等，它们不相同
        if (p.val != q.val) {
            return false;
        }
        // 递归比较左子树和右子树
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }
}

 首先，它检查两棵树是否都为空，如果是，则它们相同。然后，它检查如果只有一棵树为空，那么它们不相同。接下来，它比较根节点的值，如果不相等，则它们不相同。最后，它递归地比较左子树和右子树。如果左右子树都相同，那么整棵树相同。这个方法会递归地在树的每个节点上执行相同的比较操作。

2. 另一颗树的子树

给你两棵二叉树 root 和 subRoot 。检验 root 中是否包含和 subRoot 具有相同结构和节点值的子树。如果存在，返回 true ；否则，返回 false 。
二叉树 tree 的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree 也可以看做它自身的一棵子树。

力扣：https://leetcode.cn/problems/subtree-of-another-tree/

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (root == null) {
            return false;
        }
        if (isSameTree(root, subRoot)) {
            return true;
        }
        return isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
    }
    
    private boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null || q == null) {
            return false;
        }
        if (p.val != q.val) {
            return false;
        }
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }
}

该方法isSubtree首先检查root是否为空，如果为空，则返回false。然后，它调用isSameTree方法来比较root和subRoot是否相同。如果相同，则返回true。如果不同，则递归地在root的左子树和右子树中继续查找subRoot。如果左子树或右子树中存在与subRoot相同的子树，则返回true。如果遍历完整棵树后仍未找到相同的子树，则返回false。

isSameTree方法是之前回答中的相同树比较方法，用于判断两棵树是否在结构上相同且节点值相同。

3. 翻转二叉树

给你一棵二叉树的根节点 root ，翻转这棵二叉树，并返回其根节点。

力扣：226. 翻转二叉树 - 力扣（Leetcode）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode invertTree(TreeNode root) {
        if (root == null) {
            return null;
        }
        // 递归地翻转左右子树
        TreeNode left = invertTree(root.left);
        TreeNode right = invertTree(root.right);
        // 交换左右子树
        root.left = right;
        root.right = left;
        return root;
    }
}

该方法invertTree首先检查根节点是否为空，如果为空，则返回null。然后，它递归地翻转左子树和右子树，将返回的翻转后的左子树和右子树赋值给根节点的右子树和左子树。最后，返回根节点，完成整棵二叉树的翻转。

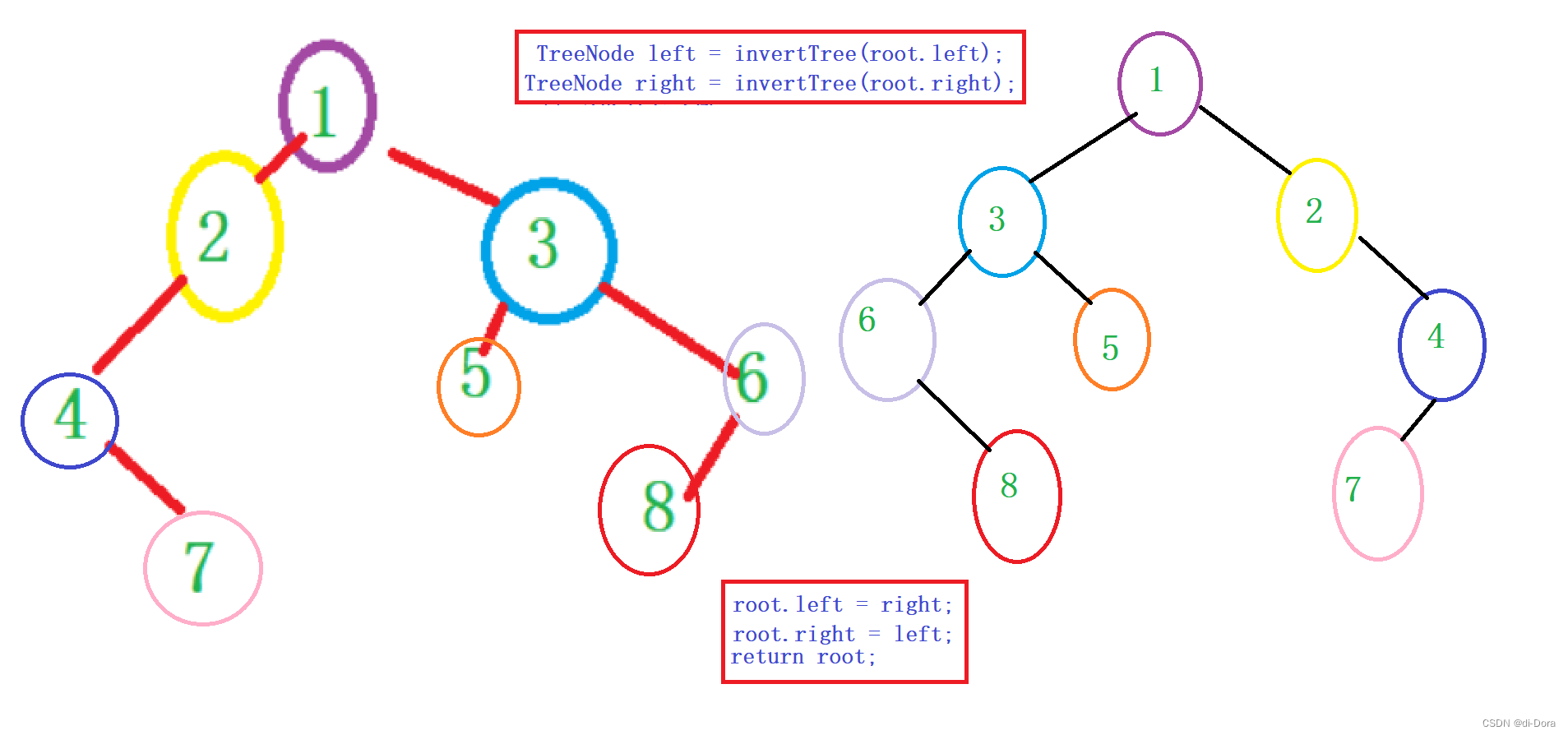
 我们通过递归地在每个节点上执行相同的翻转操作，可以实现对整棵二叉树的翻转。

4. 判断一颗二叉树是否是平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。
本题中，一棵高度平衡二叉树定义为：
一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

力扣：110. 平衡二叉树 - 力扣（Leetcode）

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isBalanced(TreeNode root) {
        if (root == null) {
            return true;
        }
        // 检查当前节点的左右子树的高度差是否超过1
        if (Math.abs(getHeight(root.left) - getHeight(root.right)) > 1) {
            return false;
        }
        // 递归地检查左子树和右子树是否都是高度平衡的
        return isBalanced(root.left) && isBalanced(root.right);
    }
    
    private int getHeight(TreeNode node) {
        if (node == null) {
            return 0;
        }
        // 递归地计算节点的高度
        int leftHeight = getHeight(node.left);
        int rightHeight = getHeight(node.right);
        // 返回节点的高度（左右子树中较大的高度加上1）
        return Math.max(leftHeight, rightHeight) + 1;
    }
}

该方法isBalanced首先检查根节点是否为空，如果为空，则认为它是高度平衡的。然后，它检查当前节点的左右子树的高度差是否超过1。如果超过1，则返回false。如果未超过1，则递归地检查左子树和右子树是否都是高度平衡的。其中，getHeight方法用于递归地计算节点的高度。对于空节点，高度为0；对于非空节点，高度为左右子树中较大的高度加上1。

通过递归地在每个节点上执行高度平衡检查，可以判断一棵二叉树是否是高度平衡的。

5. 对称二叉树

给你一个二叉树的根节点 root ， 检查它是否轴对称。

力扣：101. 对称二叉树 - 力扣（Leetcode） 

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean isSymmetric(TreeNode root) {
        if (root == null) {
            return true;
        }
        return isMirror(root.left, root.right);
    }
    
    private boolean isMirror(TreeNode left, TreeNode right) {
        if (left == null && right == null) {
            return true;
        }
        if (left == null || right == null || left.val != right.val) {
            return false;
        }
        return isMirror(left.left, right.right) && isMirror(left.right, right.left);
    }
}

该方法isSymmetric首先检查根节点是否为空，如果为空，则认为它是轴对称的。然后，它调用isMirror方法来判断左子树和右子树是否是镜像对称的。isMirror方法中，它首先检查左右节点是否同时为空，如果是，则认为它们是镜像对称的。然后，它检查左右节点是否有一个为空或者值不相等，如果是，则认为它们不是镜像对称的。最后，它递归地判断左子树的左节点和右子树的右节点是否是镜像对称的，并且判断左子树的右节点和右子树的左节点是否是镜像对称的。如果左右子树都是镜像对称的，那么整棵树是轴对称的。

通过递归地在每个节点上执行镜像对称性检查，可以判断一棵二叉树是否是轴对称的。

6. 二叉树的构建及遍历

 编一个程序，读入用户输入的一串先序遍历字符串，根据此字符串建立一个二叉树（以指针方式存储）。 例如如下的先序遍历字符串： ABC##DE#G##F### 其中“#”表示的是空格，空格字符代表空树。建立起此二叉树以后，再对二叉树进行中序遍历，输出遍历结果。
输入描述：
输入包括1行字符串，长度不超过100。
输出描述：
可能有多组测试数据，对于每组数据， 输出将输入字符串建立二叉树后中序遍历的序列，每个字符后面都有一个空格。 每个输出结果占一行。

牛客：二叉树遍历_牛客题霸_牛客网 (nowcoder.com)

import java.util.Scanner;

    static class TreeNode {
        char val;
        TreeNode left;
        TreeNode right;

        TreeNode(char val) {
            this.val = val;
        }
    }


        private static int index = 0;

        public static void main(String[] args) {
            Scanner in = new Scanner(System.in);
            while (in.hasNextLine()) {  // 循环读取输入的每一行
                String preorder = in.nextLine();  // 读取先序遍历字符串
                TreeNode root = buildTree(preorder);  // 构建二叉树
                String inorder = inorderTraversal(root);  // 中序遍历二叉树
                System.out.println(inorder);  // 打印中序遍历结果
            }
        }

        private static TreeNode buildTree(String preorder) {
            index = 0;  // 重置索引为0
            return buildTreeHelper(preorder);  // 调用辅助方法构建二叉树
        }

        private  static  TreeNode buildTreeHelper(String preorder) {
            if (index >= preorder.length()) {  // 如果索引超出字符串长度，表示已遍历完，返回null
                return null;
            }

            char ch = preorder.charAt(index++);  // 获取当前字符，并将索引增加1
            if (ch == '#') {  // 如果当前字符是'#'，表示是空节点，返回null
                return null;
            }

            TreeNode node = new TreeNode(ch);  // 创建新的二叉树节点
            node.left = buildTreeHelper(preorder);  // 递归构建左子树
            node.right = buildTreeHelper(preorder);  // 递归构建右子树

            return node;  // 返回构建好的节点
        }

        private static String inorderTraversal(TreeNode root) {
            StringBuilder sb = new StringBuilder();  // 创建StringBuilder对象，用于保存中序遍历结果
            inorderTraversalHelper(root, sb);  // 调用辅助方法进行中序遍历
            return sb.toString();  // 返回中序遍历结果的字符串形式
        }

        private static void inorderTraversalHelper(TreeNode node, StringBuilder sb) {
            if (node == null) {  // 如果节点为空，表示到达叶子节点，直接返回
                return;
            }

            inorderTraversalHelper(node.left, sb);  // 递归遍历左子树
            sb.append(node.val).append(" ");  // 将当前节点值添加到结果中
            inorderTraversalHelper(node.right, sb);  // 递归遍历右子树
        }

这个程序首先读取用户输入的一串先序遍历字符串。然后使用buildTree函数根据该字符串建立二叉树，并使用inorderTraversal函数进行中序遍历。buildTree函数使用递归的方式构建二叉树，每次取出字符串中的一个字符，如果是#表示空树，则返回null，否则创建一个新的节点，并递归构建其左子树和右子树。inorderTraversal函数使用递归的方式进行中序遍历，先遍历左子树，然后将当前节点的值添加到结果字符串中，最后遍历右子树。

通过这个程序，可以根据输入的先序遍历字符串建立二叉树，并输出中序遍历的结果。每个字符后面都有一个空格，每个输出结果占一行。

7. 二叉树的分层遍历

 给你二叉树的根节点 root ，返回其节点值的层序遍历 。（即逐层地，从左到右访问所有节点）。

力扣：102. 二叉树的层序遍历 - 力扣（Leetcode）

import java.util.ArrayList;
import java.util.LinkedList;
import java.util.List;
import java.util.Queue;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> result = new ArrayList<>();
        if (root == null) {
            return result;  //注意，这里如果给的是[]，那么你也要返回[]，而不是null
        }
        
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        
        while (!queue.isEmpty()) {
            int levelSize = queue.size();
            List<Integer> levelValues = new ArrayList<>();
            
            for (int i = 0; i < levelSize; i++) {
                TreeNode node = queue.poll();
                levelValues.add(node.val);
                
                if (node.left != null) {
                    queue.offer(node.left);
                }
                
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            
            result.add(levelValues);
        }
        
        return result;
    }
}

在levelOrder函数中，我们首先创建一个结果列表result来存储层序遍历的结果。然后，我们创建一个队列queue并将根节点入队。接下来，我们使用一个循环来处理每一层的节点。在循环中，我们首先获取当前层的节点数levelSize，然后创建一个列表levelValues来存储当前层的节点值。接着，我们从队列中取出levelSize个节点，将它们的值加入levelValues列表，并将它们的非空子节点加入队列。完成当前层的处理后，我们将levelValues列表加入result列表。最终，当队列为空时，我们完成了二叉树的层序遍历。

通过这个程序，可以获得二叉树节点值的层序遍历结果，并将其存储在一个列表中返回。每个层的节点值都存储在独立的列表中，按层级顺序排列。

8. 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先

 给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。
百度百科中最近公共祖先的定义为：“对于有根树 T 的两个节点 p、q，最近公共祖先表示为一个节点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

力扣：236. 二叉树的最近公共祖先 - 力扣（Leetcode）

我们当然可以利用之前写过的判断是否为子树的方法来做这道题，同样也要用到递归的思想：

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q){
        if(root==null||p==null||q==null){
            return null;
        }
        if(p==root||q==root){
            return root;
        }
    if (isSubtree(root.left, p) && isSubtree(root.left, q)) {
        return lowestCommonAncestor(root.left, p, q);
    }
    if (isSubtree(root.right, p) && isSubtree(root.right, q)) {
        return lowestCommonAncestor(root.right, p, q);
    }
    return root;
    }

    public boolean isSubtree(TreeNode root, TreeNode subRoot) {
        if (root == null) {
            return false;
        }
        if (isSameTree(root, subRoot)) {
            return true;
        }
        return isSubtree(root.left, subRoot) || isSubtree(root.right, subRoot);
    }

    private boolean isSameTree(TreeNode p, TreeNode q) {
        if (p == null && q == null) {
            return true;
        }
        if (p == null || q == null) {
            return false;
        }
        if (p.val != q.val) {
            return false;
        }
        return isSameTree(p.left, q.left) && isSameTree(p.right, q.right);
    }
}

但是这个方法的时间复杂度太大了： 

所以我们换个思路： 

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int x) {
        val = x;
    }
}

class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) {
            return root;
        }
        
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        
        if (left != null && right != null) {
            return root;
        } else if (left != null) {
            return left;
        } else {
            return right;
        }
    }
}

在lowestCommonAncestor函数中，我们首先检查当前节点是否为空或等于节点p或节点q。如果是，那么当前节点就是最近公共祖先，我们直接返回该节点。否则，我们分别在左子树和右子树中递归寻找最近公共祖先。如果左子树和右子树都返回非空节点，那么说明节点p和节点q分别在当前节点的左子树和右子树中，当前节点就是最近公共祖先。如果只有左子树返回非空节点，那么说明节点p和节点q都在左子树中，返回左子树的结果作为最近公共祖先。如果只有右子树返回非空节点，那么说明节点p和节点q都在右子树中，返回右子树的结果作为最近公共祖先。

 

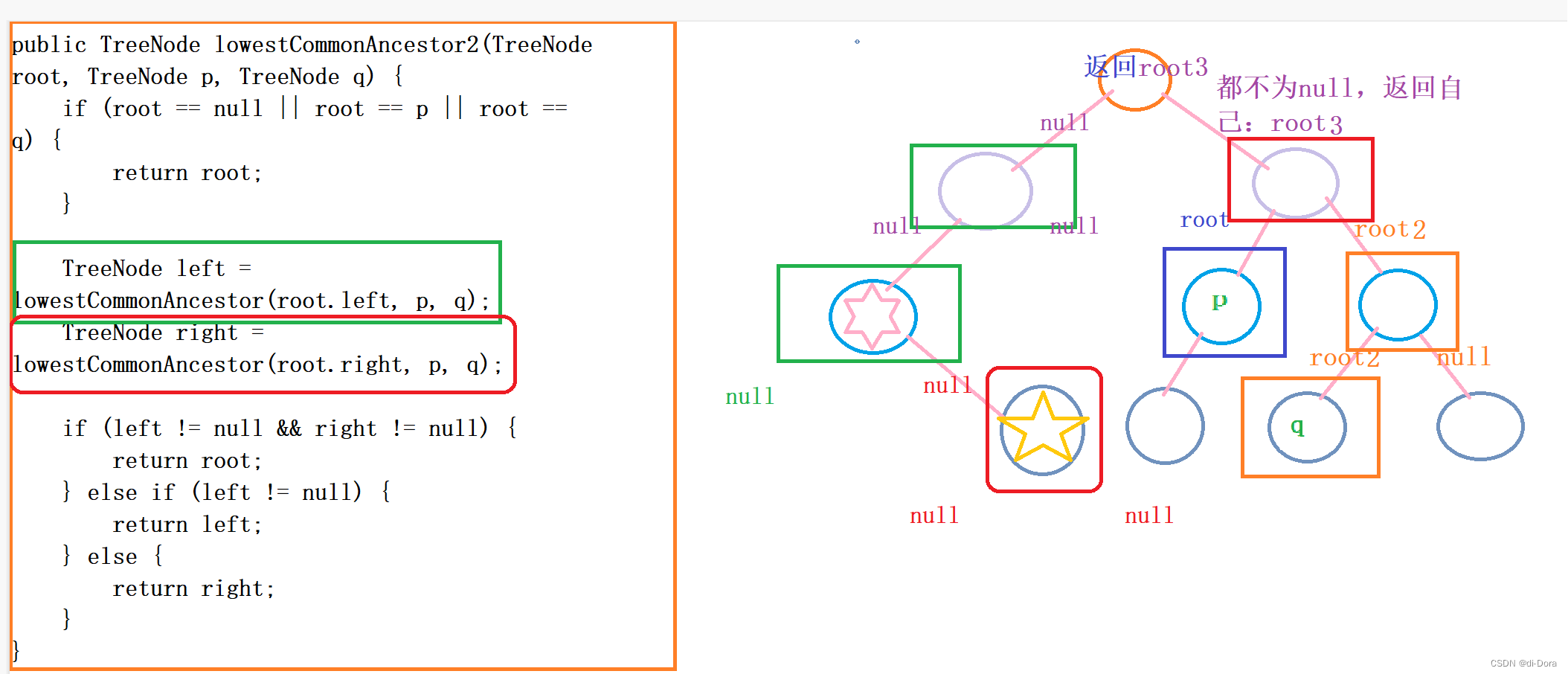
这个写法不太好理解，我建议你最好自己画一个图来感受，并且把p和q放到不同的位置来进行多次判断。 

通过这个程序，我们就可以找到二叉树中两个指定节点的最近公共祖先，并将其作为结果返回。

9. 根据一棵树的前序遍历与中序遍历构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

这个题就是我们之前的选择题的程序代码不是吗？你一定要理解之前的判断原理，才能够写出这个代码。

力扣：105. 从前序与中序遍历序列构造二叉树 - 力扣（Leetcode） 

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        return buildTreeHelper(preorder, inorder, 0, 0, inorder.length - 1);
    }
    
    private TreeNode buildTreeHelper(int[] preorder, int[] inorder, int preStart, int inStart, int inEnd) {
        if (preStart > preorder.length - 1 || inStart > inEnd) {
            return null;
        }
        
        TreeNode root = new TreeNode(preorder[preStart]);
        
        int inIndex = 0;
        for (int i = inStart; i <= inEnd; i++) {
            if (inorder[i] == root.val) {
                inIndex = i;
                break;
            }
        }
        
        root.left = buildTreeHelper(preorder, inorder, preStart + 1, inStart, inIndex - 1);
        root.right = buildTreeHelper(preorder, inorder, preStart + inIndex - inStart + 1, inIndex + 1, inEnd);
        
        return root;
    }
}

在buildTree函数中，我们调用辅助函数buildTreeHelper来构建二叉树。辅助函数接受先序遍历数组preorder、中序遍历数组inorder，以及先序遍历的起始位置preStart、中序遍历的起始位置inStart和结束位置inEnd作为参数。首先，我们检查基准情况，如果preStart大于先序遍历数组的最大索引值或inStart大于inEnd，则返回null，表示空树。否则，我们创建一个根节点，值为preorder[preStart]。接下来，我们在中序遍历数组inorder中找到根节点的索引inIndex，然后根据inIndex将中序遍历数组分为左子树和右子树。递归地构建左子树和右子树，并将它们分别作为根节点的左孩子和右孩子。最后，返回根节点。

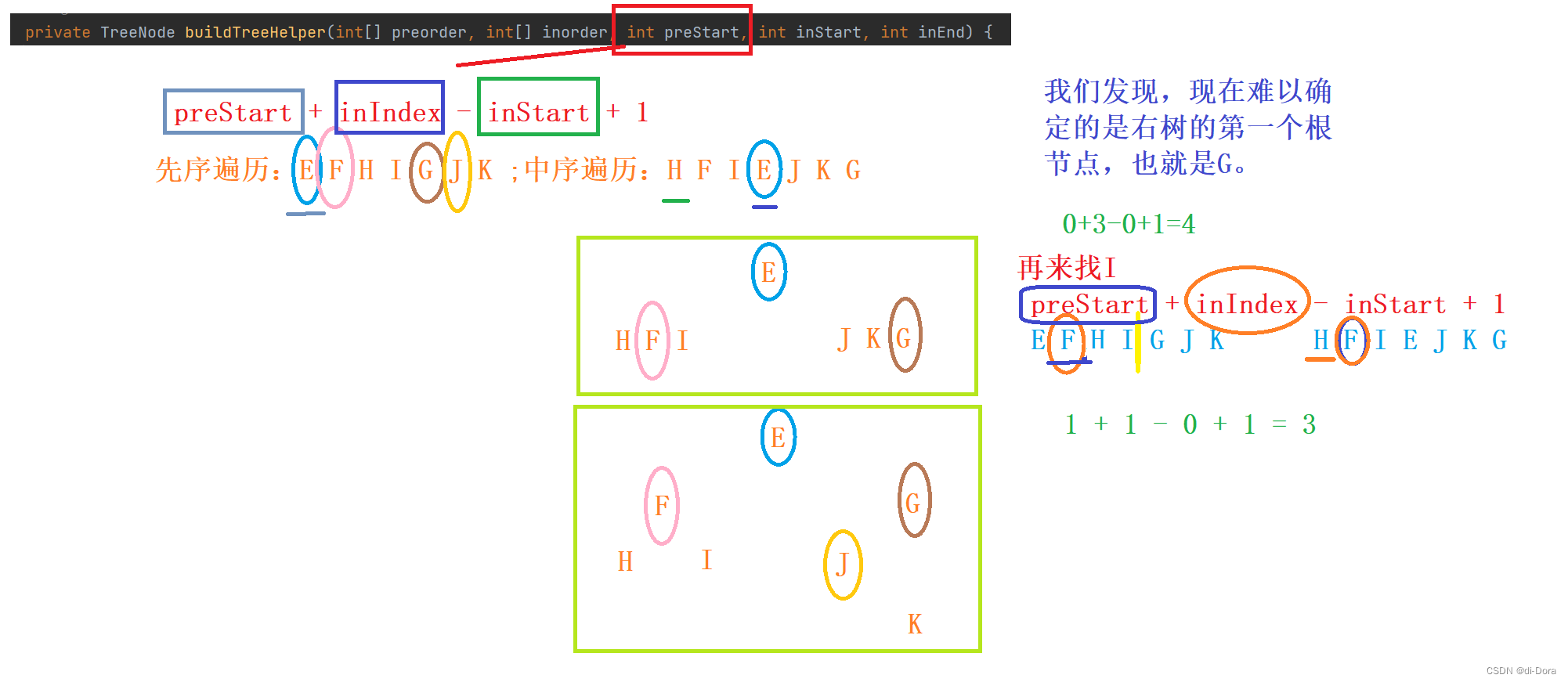
这里面，preStart + inIndex - inStart + 1 或许需要作出一些解释：

我们首先需要明确一个点——我们现在在干什么？我们在创建右子树。

这里的右子树有什么？以图上的树为例：我们有以E作为根节点的J、K、G形成的右子树，有以F为根节点的 I 形成的右子树。

所以，preStart其实是我们用来确定此次根节点的指标。也就是说，此次的前序遍历是从preStart开始的，而前序遍历里面第一个节点就是根节点。我们最终需要得到的“ preStart + inIndex - inStart + 1 ” 就是在前序遍历里面的坐标。

接下来的“inIndex - inStart” 是中序遍历里面本次的根节点距离本次子树的中序遍历开头节点的相对距离（每调用一遍这个方法，都会生成新的Index）。

最后+1，代表坐标后挪一位，是我们中序遍历里面紧挨着中间节点的“左根右”里的右子树的根节点。

通过这个程序，可以根据先序遍历数组和中序遍历数组构造二叉树，并返回根节点。

 力扣的官方题解还给出了另一种奇特的办法——迭代，但是不是很好理解，你需要多看一会儿，优点是，它的时间复杂度很低（我建议你去看看力扣的官方的解析，比较多，我就不粘贴过来了，前面已经放了链接）：

class Solution {
    public TreeNode buildTree(int[] preorder, int[] inorder) {
        if (preorder == null || preorder.length == 0) {
            return null;
        }
        TreeNode root = new TreeNode(preorder[0]);
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        stack.push(root);
        int inorderIndex = 0;
        for (int i = 1; i < preorder.length; i++) {
            int preorderVal = preorder[i];
            TreeNode node = stack.peek();
            if (node.val != inorder[inorderIndex]) {
                node.left = new TreeNode(preorderVal);
                stack.push(node.left);
            } else {
                while (!stack.isEmpty() && stack.peek().val == inorder[inorderIndex]) {
                    node = stack.pop();
                    inorderIndex++;
                }
                node.right = new TreeNode(preorderVal);
                stack.push(node.right);
            }
        }
        return root;
    }
}

10. 根据一棵树的中序遍历与后序遍历构造二叉树

 给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗二叉树 。

这题和刚刚的没有什么太大的区别，无非是前序遍历和后序遍历的不同。

力扣：106. 从中序与后序遍历序列构造二叉树 - 力扣（Leetcode）

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public TreeNode buildTree(int[] inorder, int[] postorder) {
        return buildTreeHelper(inorder, postorder, 0, inorder.length - 1, postorder.length - 1);
    }
    
    private TreeNode buildTreeHelper(int[] inorder, int[] postorder, int inStart, int inEnd, int postEnd) {
        if (inStart > inEnd || postEnd < 0) {
            return null;
        }
        
        TreeNode root = new TreeNode(postorder[postEnd]);
        
        int inIndex = 0;
        for (int i = inStart; i <= inEnd; i++) {
            if (inorder[i] == root.val) {
                inIndex = i;
                break;
            }
        }
        
        root.right = buildTreeHelper(inorder, postorder, inIndex + 1, inEnd, postEnd - 1);
        root.left = buildTreeHelper(inorder, postorder, inStart, inIndex - 1, postEnd - (inEnd - inIndex) - 1);
        
        return root;
    }
}

在buildTree函数中，我们调用辅助函数buildTreeHelper来构建二叉树。辅助函数接受中序遍历数组inorder、后序遍历数组postorder，以及中序遍历的起始位置inStart和结束位置inEnd，以及后序遍历的结束位置postEnd作为参数。首先，我们检查基准情况，如果inStart大于inEnd或postEnd小于0，则返回null，表示空树。否则，我们创建一个根节点，值为postorder[postEnd]。接下来，我们在中序遍历数组inorder中找到根节点的索引inIndex，然后根据inIndex将中序遍历数组分为左子树和右子树。递归地构建右子树和左子树，并将它们分别作为根节点的右孩子和左孩子。最后，返回根节点。

这里就和前面反过来了，右树比较好确定，左树的话就比较难确定：

通过这个程序，就可以根据中序遍历数组和后序遍历数组构造二叉树，并返回根节点。

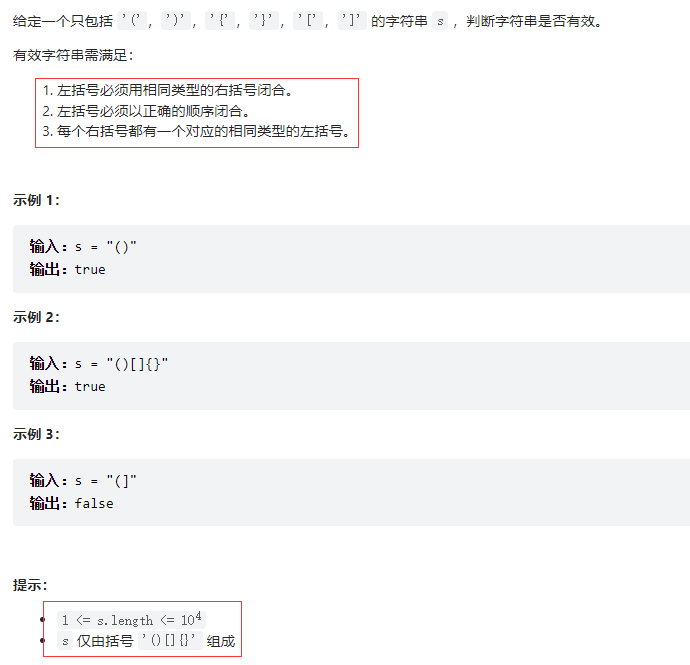
11. 二叉树创建字符串

 给你二叉树的根节点 root ，请你采用前序遍历的方式，将二叉树转化为一个由括号和整数组成的字符串，返回构造出的字符串。
空节点使用一对空括号对 "()" 表示，转化后需要省略所有不影响字符串与原始二叉树之间的一对一映射关系的空括号对。

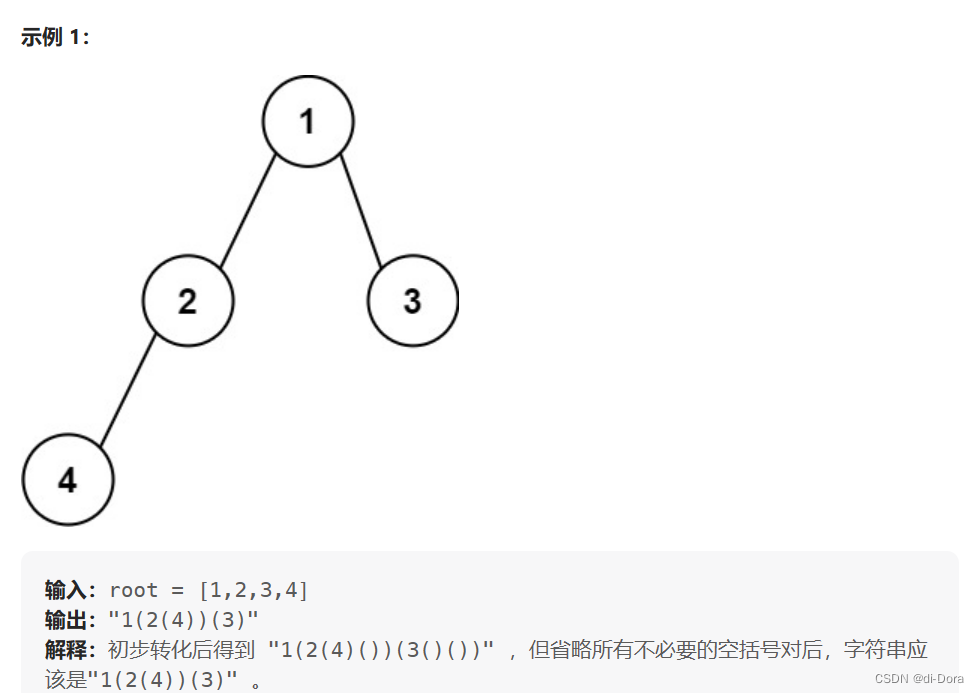
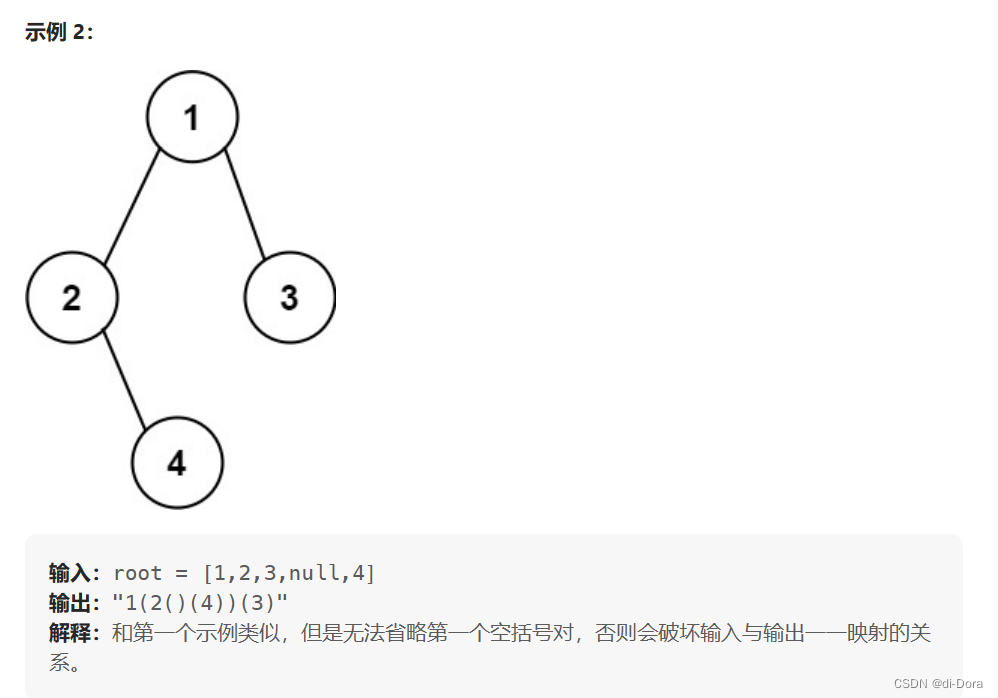 力扣：606. 根据二叉树创建字符串 - 力扣（Leetcode）

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public String tree2str(TreeNode root) {
        if (root == null) {
            return "";
        }
        
        StringBuilder sb = new StringBuilder();
        tree2strHelper(root, sb);
        return sb.toString();
    }
    
    private void tree2strHelper(TreeNode root, StringBuilder sb) {
        if (root == null) {
            return;
        }
        
        sb.append(root.val);
        
        if (root.left != null || root.right != null) {
            sb.append("(");
            tree2strHelper(root.left, sb);
            sb.append(")");
        }
        
        if (root.right != null) {
            sb.append("(");
            tree2strHelper(root.right, sb);
            sb.append(")");
        }
    }
}

在tree2str函数中，我们首先检查根节点是否为空，如果为空则返回空字符串。否则，我们创建一个StringBuilder对象sb用于构建结果字符串，并调用辅助函数tree2strHelper来进行递归遍历。辅助函数接受当前节点root和StringBuilder对象sb作为参数。首先，我们将当前节点的值添加到sb中。然后，我们检查当前节点的左子树和右子树是否存在。如果至少一个子树存在，我们在结果字符串中添加一个左括号"("，然后递归处理左子树，并在结果字符串中添加一个右括号")"。如果右子树存在，我们再次在结果字符串中添加一个左括号"("，然后递归处理右子树，并在结果字符串中添加一个右括号")"。通过这样的方式，我们可以按照前序遍历的顺序将二叉树转化为字符串。

力扣给的官方题解更简洁，直接区分了两种情况：没有右子树的需要省略空括号的，可能没有左子树的不能省略空括号的大部分情况（我稍微拆开了了一点，方便看）：

class Solution {
    public String tree2str(TreeNode root) {
        if (root == null) {
            return "";
        }
        if (root.left == null && root.right == null) {
            return Integer.toString(root.val);
        }
        if (root.right == null) {
            return new StringBuffer().append(root.val)
                                     .append("(")
                                     .append(tree2str(root.left))
                                     .append(")")
                                     .toString();
        }

        return new StringBuffer().append(root.val)
                                 .append("(")
                                 .append(tree2str(root.left))
                                 .append(")(")
                                 .append(tree2str(root.right))
                                 .append(")")
                                 .toString();
        }
}

这样，我们就可以将二叉树按照前序遍历的方式转化为字符串，并返回构造出的字符串。

12. 二叉树前序非递归遍历实现

 给你二叉树的根节点 root ，返回它节点值的 前序 遍历。

力扣：144. 二叉树的前序遍历 - 力扣（Leetcode）

1、递归（我们写过了）

import java.util.ArrayList;
import java.util.List;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        preorderTraversalHelper(root, result);
        return result;
    }
    
    private void preorderTraversalHelper(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        
        result.add(root.val);
        preorderTraversalHelper(root.left, result);
        preorderTraversalHelper(root.right, result);
    }
}

2、迭代

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }
        
        Stack<TreeNode> stack = new Stack<>();
        stack.push(root);
        
        while (!stack.isEmpty()) {
            TreeNode node = stack.pop();
            result.add(node.val);
            
            if (node.right != null) {
                stack.push(node.right);
            }
            
            if (node.left != null) {
                stack.push(node.left);
            }
        }
        
        return result;
    }
}

 注意，这里前序遍历是“根左右”，而先压入栈中的元素是最后出栈的，所以我们先把右子树压进去，再压左子树。

13. 二叉树中序非递归遍历实现

 给定一个二叉树的根节点 root ，返回 它的 中序 遍历。

力扣：94. 二叉树的中序遍历 - 力扣（Leetcode）

1、递归

import java.util.ArrayList;
import java.util.List;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        inorderTraversalHelper(root, result);
        return result;
    }
    
    private void inorderTraversalHelper(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        
        inorderTraversalHelper(root.left, result);
        result.add(root.val);
        inorderTraversalHelper(root.right, result);
    }
}

2、迭代

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }
        
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        
        while (curr != null || !stack.isEmpty()) {
            while (curr != null) {
                stack.push(curr);
                curr = curr.left;
            }
            
            curr = stack.pop();
            result.add(curr.val);
            curr = curr.right;
        }
        
        return result;
    }
}

这个代码值得好好品一下。 

 14. 二叉树后序非递归遍历实现

给你一棵二叉树的根节点 root ，返回其节点值的 后序遍历 。

力扣：145. 二叉树的后序遍历 - 力扣（Leetcode）

1、递归

import java.util.ArrayList;
import java.util.List;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        postorderTraversalHelper(root, result);
        return result;
    }
    
    private void postorderTraversalHelper(TreeNode root, List<Integer> result) {
        if (root == null) {
            return;
        }
        
        postorderTraversalHelper(root.left, result);
        postorderTraversalHelper(root.right, result);
        result.add(root.val);
    }
}

2、迭代

import java.util.ArrayList;
import java.util.List;
import java.util.Stack;

class TreeNode {
    int val;
    TreeNode left;
    TreeNode right;
    
    TreeNode(int val) {
        this.val = val;
    }
}

class Solution {
    public List<Integer> postorderTraversal(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        if (root == null) {
            return result;
        }
        
        Stack<TreeNode> stack = new Stack<>();
        TreeNode curr = root;
        TreeNode lastVisited = null;
        
        while (curr != null || !stack.isEmpty()) {
            while (curr != null) {
                stack.push(curr);
                curr = curr.left;
            }
            
            TreeNode peekNode = stack.peek();
            
            if (peekNode.right == null || peekNode.right == lastVisited) {
                result.add(peekNode.val);
                lastVisited = stack.pop();
            } else {
                curr = peekNode.right;
            }
        }
        
        return result;
    }
}

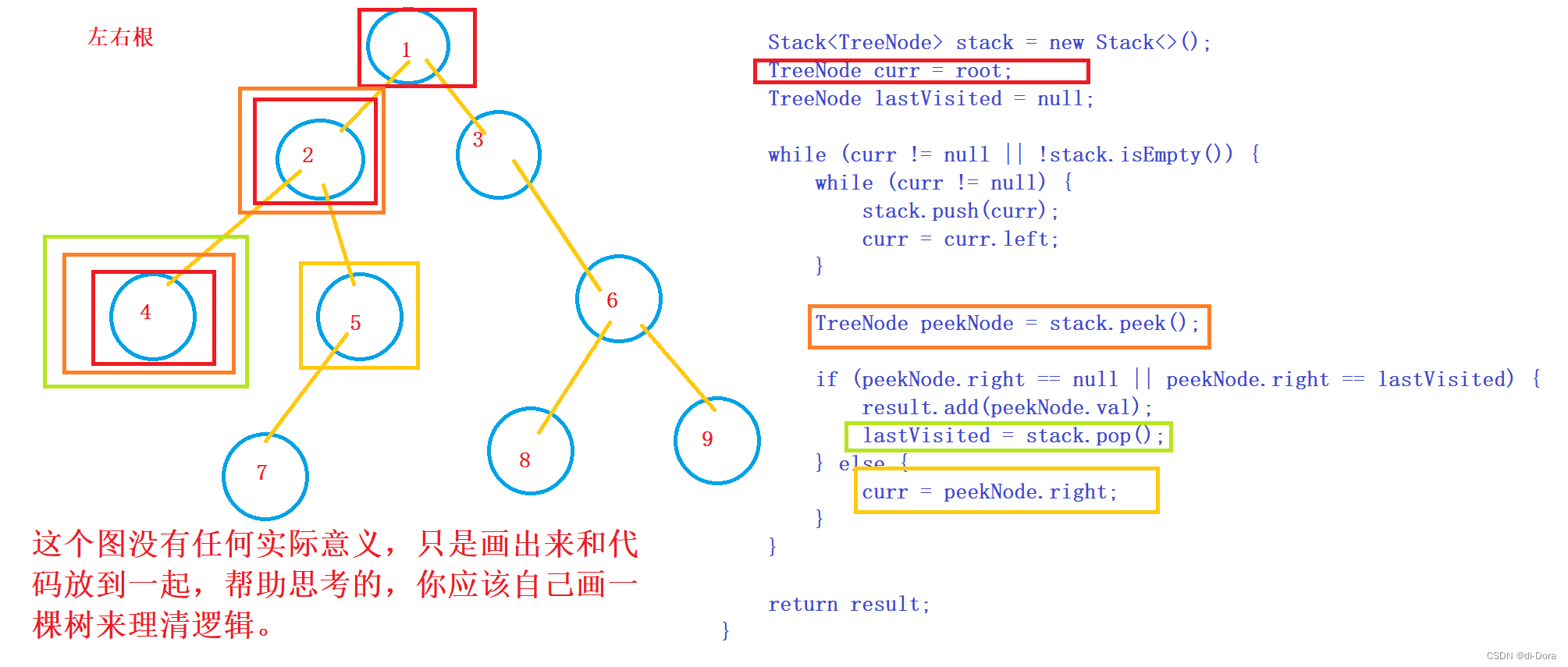
逐步压栈，直到找到最左边的元素，再去看看它有没有右子树。没有右子树的话，就相当于它是一个叶子节点，可以压到结果栈里面了。有的话就代表它不是叶子节点，而是一个有右子树的根节点，因为后序遍历是先右边再为根，所以再去定位右边子树为新的节点，去找它的最左边。
因为压栈就等于已经保存了一个逐次调用的顺序了，所以我们可以逐次弹出每一层的主节点，在依次去每次判断每个节点的右子树的情况。