目录
- 0 写在前面
- 1 串行集成学习
- 2 AdaBoost原理推导
- 3 Python实现
- 3.1 算法流程
- 3.2 核心代码
- 3.3 可视化
0 写在前面
机器学习强基计划聚焦深度和广度,加深对机器学习模型的理解与应用。“深”在详细推导算法模型背后的数学原理;“广”在分析多个机器学习模型:决策树、支持向量机、贝叶斯与马尔科夫决策、强化学习等。强基计划实现从理论到实践的全面覆盖,由本人亲自从底层编写、测试与文章配套的各个经典算法,不依赖于现有库,可以大大加深对算法的理解。
🚀详情:机器学习强基计划(附几十种经典模型源码)
1 串行集成学习
串行集成学习是一种机器学习的技术,旨在通过将多个基学习器按顺序组合起来,以提高整体学习性能。在串行集成学习中,基学习器按照一定的顺序进行训练和集成,每个基学习器都依赖于前一个学习器的输出。
Boosting是一族将弱学习器提升为强学习器的串行集成算法,这族算法核心原理为:先从初始训练集训练出一个基学习器;再根据基学习器的表现对训练样本分布进行调整,实现不同学习器的差异性,同时使先前基学习器的误分类样本在后续受到更多关注;然后基于调整后的样本分布训练下一个基学习器;重复进行直至基学习器数目达到事先指定值 T T T,最终将这 T T T个基学习器进行集成输出。

Boosting族的著名算法是自适应提升(Adaptive Boosting, AdaBoost),其采用指数损失函数,具体原理参见第二节
2 AdaBoost原理推导
AdaBoost具体而言,分为两个步骤:
- 从样本分布 D t \mathcal{D} _t Dt中训练分类器 h t h_t ht,使 H t − 1 H_{t-1} Ht−1的误分类样本在 h t h_t ht作用下误分类概率下降
- 生成 h t h_t ht后计算其权重 α t \alpha _t αt使总体损失最小
注意,标准AdaBoost算法只用于二分类问题。
具体原理推导如下:首先考察 h t h_t ht的产生,理想的 h t h_t ht能纠正 H t − 1 H_{t-1} Ht−1的所有错误,使损失最小
h t = a r g min h ∈ H ∑ x e − f ( x ) [ H t − 1 ( x ) + α t h ( x ) ] = a r g min h ∈ H ∑ x : h ( x ) = f ( x ) e − f ( x ) H t − 1 ( x ) e − α t + ∑ x : h ( x ) ≠ f ( x ) e − f ( x ) H t − 1 ( x ) e α t = a r g min h ∈ H ∑ x e − f ( x ) H t − 1 ( x ) e − α t + ∑ x : h ( x ) ≠ f ( x ) e − f ( x ) H t − 1 ( x ) ( e α t − e − α t ) = a r g min h ∈ H ∑ x : h ( x ) ≠ f ( x ) e − f ( x ) H t − 1 ( x ) = a r g min h ∈ H ∑ x : h ( x ) ≠ f ( x ) e − f ( x ) H t − 1 ( x ) ∑ x e − f ( x ) H t − 1 ( x ) \begin{aligned}h_t&=\underset{h\in \mathcal{H}}{\mathrm{arg}\min}\sum_{\boldsymbol{x}}{e^{-f\left( \boldsymbol{x} \right) \left[ H_{t-1}\left( \boldsymbol{x} \right) +\alpha _th\left( \boldsymbol{x} \right) \right]}}\\&=\underset{h\in \mathcal{H}}{\mathrm{arg}\min}\sum_{\boldsymbol{x}:h\left( \boldsymbol{x} \right) =f\left( \boldsymbol{x} \right)}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}e^{-\alpha _t}}+\sum_{\boldsymbol{x}:h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right)}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}e^{\alpha _t}}\\&=\underset{h\in \mathcal{H}}{\mathrm{arg}\min}\sum_{\boldsymbol{x}}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}e^{-\alpha _t}}+\sum_{\boldsymbol{x}:h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right)}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}\left( e^{\alpha _t}-e^{-\alpha _t} \right)}\\&=\underset{h\in \mathcal{H}}{\mathrm{arg}\min}\sum_{\boldsymbol{x}:h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right)}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}\\&=\underset{h\in \mathcal{H}}{\mathrm{arg}\min}\sum_{\boldsymbol{x}:h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right)}{\frac{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}{\sum\nolimits_{\boldsymbol{x}}^{}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}}}\end{aligned} ht=h∈Hargminx∑e−f(x)[Ht−1(x)+αth(x)]=h∈Hargminx:h(x)=f(x)∑e−f(x)Ht−1(x)e−αt+x:h(x)=f(x)∑e−f(x)Ht−1(x)eαt=h∈Hargminx∑e−f(x)Ht−1(x)e−αt+x:h(x)=f(x)∑e−f(x)Ht−1(x)(eαt−e−αt)=h∈Hargminx:h(x)=f(x)∑e−f(x)Ht−1(x)=h∈Hargminx:h(x)=f(x)∑∑xe−f(x)Ht−1(x)e−f(x)Ht−1(x)
其中 f f f为训练集 D D D中样本 x \boldsymbol{x} x到其标签 y y y的映射。若设分布
D t ( x ) = e − f ( x ) H t − 1 ( x ) ∑ x e − f ( x ) H t − 1 ( x ) \mathcal{D} _t\left( \boldsymbol{x} \right) =\frac{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}{\sum\nolimits_{\boldsymbol{x}}^{}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}} Dt(x)=∑xe−f(x)Ht−1(x)e−f(x)Ht−1(x)
其中误分类样本 f ( x ) H t − 1 ( x ) < 0 f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right) <0 f(x)Ht−1(x)<0权重升高,正确分类样本权重降低,则
h t = a r g min h ∈ H ∑ x : h ( x ) ≠ f ( x ) D t ( x ) = a r g min h ∈ H P x D t ( h ( x ) ≠ f ( x ) ) h_t=\underset{h\in \mathcal{H}}{\mathrm{arg}\min}\sum_{\boldsymbol{x}:h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right)}{\mathcal{D} _t\left( \boldsymbol{x} \right)}=\underset{h\in \mathcal{H}}{\mathrm{arg}\min}P_{\boldsymbol{x}~\mathcal{D} _t}\left( h\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right) \right) ht=h∈Hargminx:h(x)=f(x)∑Dt(x)=h∈HargminPx Dt(h(x)=f(x))
换言之,只要根据 H t − 1 H_{t-1} Ht−1调整下一轮迭代时的样本分布 D t ( x ) \mathcal{D} _t\left( \boldsymbol{x} \right) Dt(x),就能降低 H t − 1 H_{t-1} Ht−1中误分类样本再次被误分类的概率。考虑迭代性,有
D t ( x ) = D t − 1 ( x ) ∑ x e − f ( x ) H t − 2 ( x ) ∑ x e − f ( x ) H t − 1 ( x ) e − f ( x ) H t − 1 ( x ) e − f ( x ) H t − 2 ( x ) = D t − 1 ( x ) e − f ( x ) α t − 1 h t − 1 ( x ) ∑ x D t − 1 ( x ) e − f ( x ) α t − 1 h t − 1 ( x ) \mathcal{D} _t\left( \boldsymbol{x} \right) =\mathcal{D} _{t-1}\left( \boldsymbol{x} \right) \frac{\sum\nolimits_{\boldsymbol{x}}^{}{e^{-f\left( \boldsymbol{x} \right) H_{t-2}\left( \boldsymbol{x} \right)}}}{\sum\nolimits_{\boldsymbol{x}}^{}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}}\frac{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}{e^{-f\left( \boldsymbol{x} \right) H_{t-2}\left( \boldsymbol{x} \right)}}=\frac{\mathcal{D} _{t-1}\left( \boldsymbol{x} \right) e^{-f\left( \boldsymbol{x} \right) \alpha _{t-1}h_{t-1}\left( \boldsymbol{x} \right)}}{\sum\nolimits_{\boldsymbol{x}}^{}{\mathcal{D} _{t-1}\left( \boldsymbol{x} \right) e^{-f\left( \boldsymbol{x} \right) \alpha _{t-1}h_{t-1}\left( \boldsymbol{x} \right)}}} Dt(x)=Dt−1(x)∑xe−f(x)Ht−1(x)∑xe−f(x)Ht−2(x)e−f(x)Ht−2(x)e−f(x)Ht−1(x)=∑xDt−1(x)e−f(x)αt−1ht−1(x)Dt−1(x)e−f(x)αt−1ht−1(x)
接下来考虑 α t \alpha _t αt的计算,同样从优化指数损失出发
α t = a r g min α e − α ∑ x : h t ( x ) = f ( x ) e − f ( x ) H t − 1 ( x ) ∑ x e − f ( x ) H t − 1 ( x ) + e α ∑ x : h t ( x ) ≠ f ( x ) e − f ( x ) H t − 1 ( x ) ∑ x e − f ( x ) H t − 1 ( x ) = a r g min α e − α ∑ x : h t ( x ) = f ( x ) D t ( x ) + e α ∑ x : h t ( x ) ≠ f ( x ) D t ( x ) = a r g min α e − α P x D t ( h t ( x ) = f ( x ) ) + e α P x D t ( h t ( x ) ≠ f ( x ) ) = η = P x D t ( h t ( x ) ≠ f ( x ) ) a r g min α e − α ( 1 − η ) + e α η \begin{aligned}\alpha _t&=\underset{\alpha}{\mathrm{arg}\min}e^{-\alpha}\sum_{\boldsymbol{x}:h_t\left( \boldsymbol{x} \right) =f\left( \boldsymbol{x} \right)}{\frac{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}{\sum\nolimits_{\boldsymbol{x}}^{}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}}}+e^{\alpha}\sum_{\boldsymbol{x}:h_t\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right)}{\frac{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}{\sum\nolimits_{\boldsymbol{x}}^{}{e^{-f\left( \boldsymbol{x} \right) H_{t-1}\left( \boldsymbol{x} \right)}}}}\\&=\underset{\alpha}{\mathrm{arg}\min}e^{-\alpha}\sum_{\boldsymbol{x}:h_t\left( \boldsymbol{x} \right) =f\left( \boldsymbol{x} \right)}{\mathcal{D} _t\left( \boldsymbol{x} \right)}+e^{\alpha}\sum_{\boldsymbol{x}:h_t\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right)}{\mathcal{D} _t\left( \boldsymbol{x} \right)}\\&=\underset{\alpha}{\mathrm{arg}\min}e^{-\alpha}P_{\boldsymbol{x}~\mathcal{D} _t}\left( h_t\left( \boldsymbol{x} \right) =f\left( \boldsymbol{x} \right) \right) +e^{\alpha}P_{\boldsymbol{x}~\mathcal{D} _t}\left( h_t\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right) \right) \\&\xlongequal{\eta =P_{\boldsymbol{x}~\mathcal{D} _t}\left( h_t\left( \boldsymbol{x} \right) \ne f\left( \boldsymbol{x} \right) \right)}\underset{\alpha}{\mathrm{arg}\min}e^{-\alpha}\left( 1-\eta \right) +e^{\alpha}\eta\end{aligned} αt=αargmine−αx:ht(x)=f(x)∑∑xe−f(x)Ht−1(x)e−f(x)Ht−1(x)+eαx:ht(x)=f(x)∑∑xe−f(x)Ht−1(x)e−f(x)Ht−1(x)=αargmine−αx:ht(x)=f(x)∑Dt(x)+eαx:ht(x)=f(x)∑Dt(x)=αargmine−αPx Dt(ht(x)=f(x))+eαPx Dt(ht(x)=f(x))η=Px Dt(ht(x)=f(x))αargmine−α(1−η)+eαη
从而
α t = 1 2 ln 1 − η η \alpha _t=\frac{1}{2}\ln \frac{1-\eta}{\eta} αt=21lnη1−η
最终结果采用加权平均法集成输出
Boosting算法要求基学习器能对特定数据分布进行学习,有两种实现方式:
- 带权学习算法:重赋权(re-weighting)——在每次迭代时根据样本分布为每个训练样本重新赋权;
- 无权学习算法:重采样(re-sampling)——在每次迭代时根据样本分布对训练集重新进行采样,再用重采样而得的样本集对基学习器进行训练。
3 Python实现
3.1 算法流程
基本流程如表所示

3.2 核心代码
核心训练代码如下
def train(self):
self.base = []
self.alpha = []
# 样本权重
w = np.ones(self.m) / self.m
data = self.data
for i in range(self.T):
# 训练个体学习器
tree = DT(data)
tree.generateTree(tree.calGainInfo, layer=1)
# 计算错误率
_, res = tree.calPredictAcc(data, tree.tree)
epi = np.sum(w[np.squeeze(np.argwhere(res==0))])
if epi > 0.5 or epi == 0:
break
# 计算分类器权重
alpha = 0.5 * np.log((1 - epi) / epi)
# 更新样本权重
res[res==0] = -1
w = w * np.exp(-alpha * res)
w = w / sum(w)
# 添加个体学习器
self.base.append(tree)
self.alpha.append(alpha)
# 基于样本权重采样(轮盘赌算法)
p0 = 0
cp = []
for j in range(self.m):
p0 = p0 + w[j]
cp.append(p0)
index = [bisect_left(cp, random.random()) for _ in range(self.m)]
data = self.data.iloc[index]
3.3 可视化
1个个体学习器的分类情况
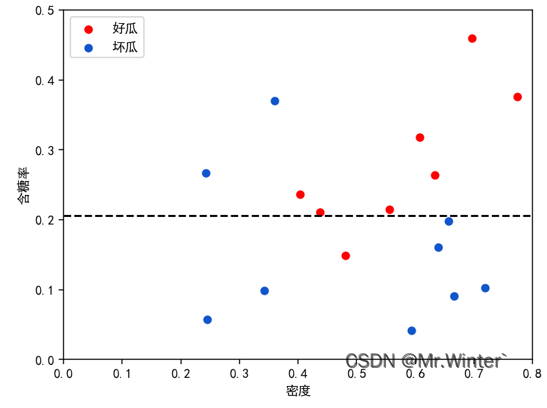
3个个体学习器的分类情况
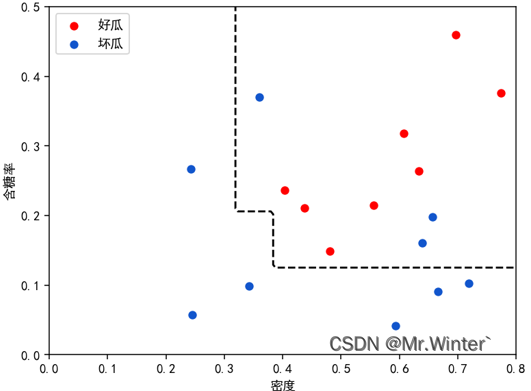
5个个体学习器的分类情况

完整代码通过下方名片联系博主获取
🔥 更多精彩专栏:
- 《ROS从入门到精通》
- 《Pytorch深度学习实战》
- 《机器学习强基计划》
- 《运动规划实战精讲》
- …