离散分类问题中的模型评价
假设分类目标只有两类:正样本(positive)和负样本(negative)。
分类器的分类结果会出现以下四种情况:
- TP: 若一个实例为正,且被预测为正,即为“真正类”(True Positive)。
- TN:若一个实例为负,且被预测为负,即为“真负类”(True Negative)。
- FP:若一个实例为负,但被预测为正,即为“假正类”(False Positive)。
- FN:若一个实例为正,但被预测为负,即为“假负类”(False Negative)。
说明:True或False表示预测正确与否。
混淆矩阵:也称误差矩阵,是分析分类器识别不同类元组的一种有用工具。
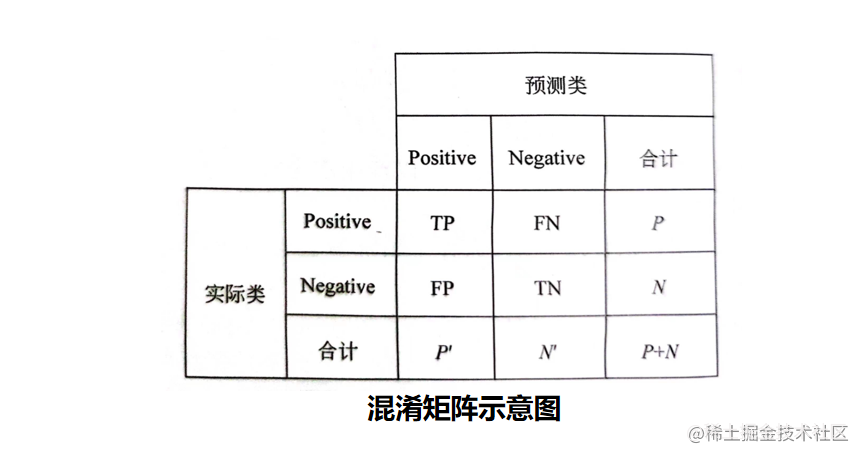
其中,每一列代表预测值,每一行代表实际的类别。
分类模型的评价指标—准确率
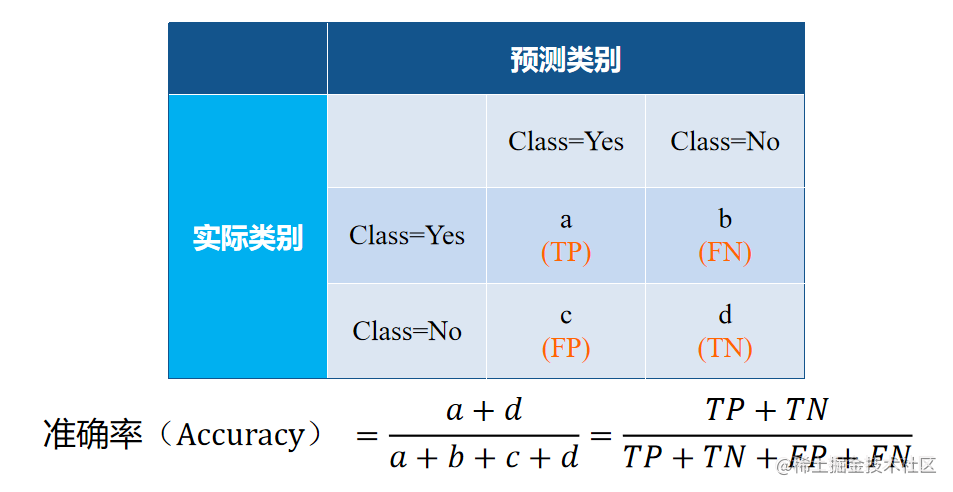
- 准确率:被准确分类的样本数占总样本数的比例。
- 准确率是评价分类模型的一个常见的评价指标。
- 一般而言,准确率越高,分类器性能越好。

- 如果模型预测每个实例为0类, 则准确率为多少?
- 显然,此时模型并不能正确预测任何1类的实例,准确率也成为了误导。特别是疾病检测中,1类更需要被关注。
- 在正负样本不平衡的情况下,准确率会有很大的缺陷。
这个时候只用准确率去评估一个模型就显得不够准确,此时就需要精确率和召回率去一起评估模型.
分类模型的评价指标—精确率
精确率(精确性的度量,也称精度):
- 针对预测结果而言,表示被预测为正的样本数中实际为正样本的比例。
- 预测为正有两种情况:一种是TP,一种是FP。

分类模型的评价指标—召回率
召回率(覆盖面的度量):
- 针对测试样本而言,表示样本集中的正样本被预测正确的比例。
- 原样本集中有两种情况:一种是TP,一种是FN

分类模型的评价指标—F1分数
对于地震的预测,我们往往希望召回率非常高,而牺牲准确率。
宁可发1000次警报,把10次地震都预测正确
也不希望发100次警报,只有8次预测正确,而漏掉2次
而对于买西瓜而言,我们往往希望买到甜的西瓜,但也存在一些不甜的西瓜。由于不可能把所有西瓜都尝一遍,所以根据常识选择一个西瓜时,
可能买到甜西瓜,此时精确率是高的;
而同时也可能把甜的误判为了不甜的,而导致了低的召回率;
这种情况要了高精确率而牺牲了召回率,因为买到了甜的西瓜,也是值得的。
- 如果一些场景下要兼顾精确率和召回率,可以使用F1分数。
- F1值是精确率和召回率的调和均值。
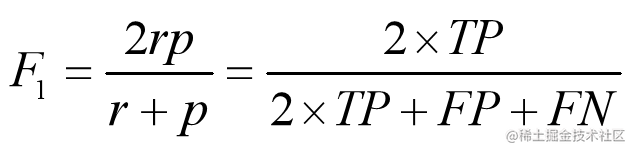
分类模型的评价指标—其它度量
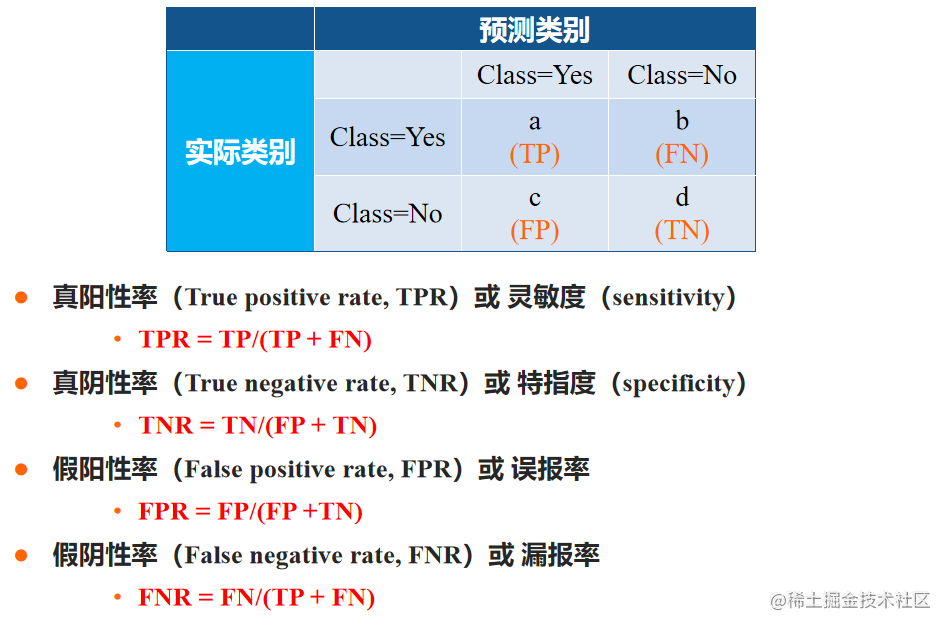
非离散分类问题中的模型评价
分类模型的评价指标— ROC曲线
-
前面讨论的分类器预测结果为离散的正类、负类,
-
如果是针对连续型数据分类,可能会得到一个数值作为分类的阈值,此时该如何进行评价呢?
-
如表所示,给出10条样本数据,对应按
朴素贝叶斯分类器得到的后验概率。如何
选定阈值以及把≥阈值的归为正类,<阈值
归为负类呢?
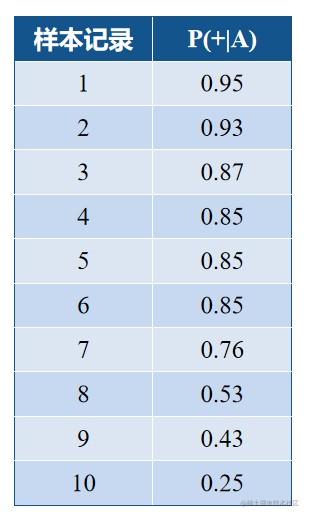
-
解决方法:连续的值离散化
-
导致的问题:离散阈值难以确定
这个时候就引出了roc曲线即受试者工作特征曲线,它是一种坐标图式的分析工具,用于: -
选择最佳的分类模型、舍弃次佳的模型。
-
在同一模型中设定最佳阈值。
-
给定一个二元分类模型和它的阈值,就能从所有样本的(阳性/阴性)真实值和预测值计算出一个 (X=FPR, Y=TPR) 坐标点。
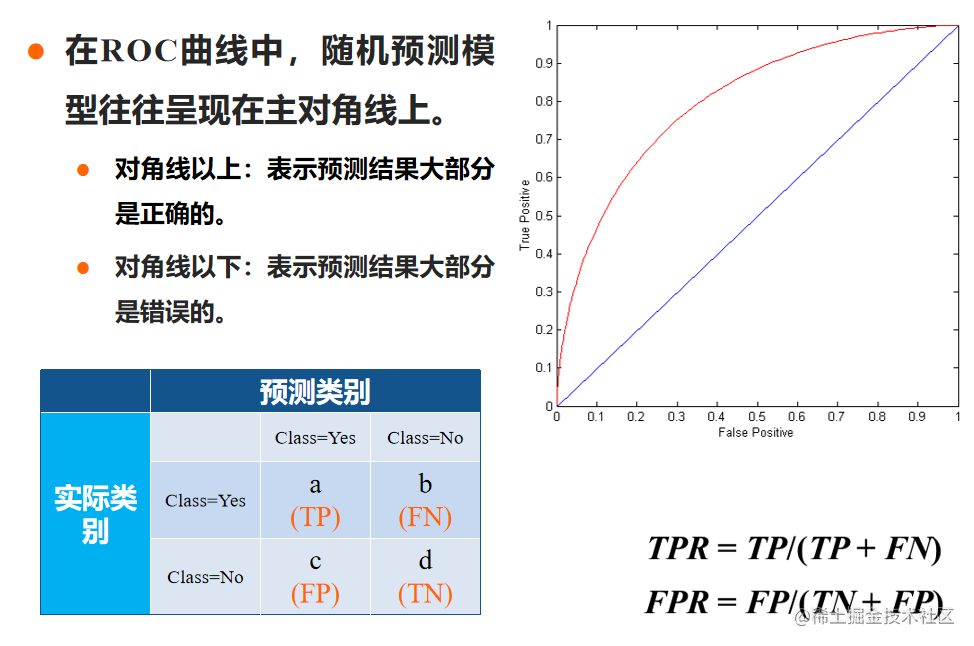
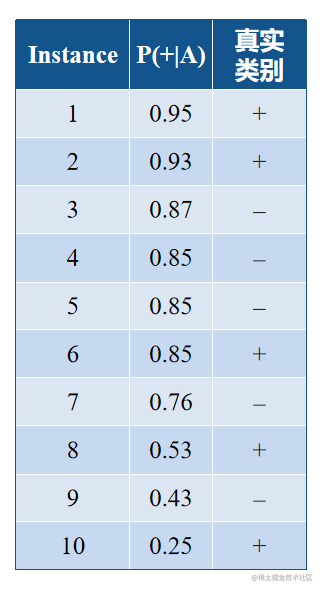
如何构建ROC曲线
- 首先利用分类器计算每个数据记录的后验概率P(+|A)
- 将这些数据记录对应的P(+|A)从高到低排列(如下表):
- 由低到高, 将每个P(+|A)值分别作为阈值,把对应的记录以及那些值高于或等于阈值指派为阳性类positive, 把那些值低于阈值指派为阴性类negative。
- 统计 TP, FP, TN, FN;
- 计算TPR 和FPR 。
- 绘出诸点(FPR, TPR)并连接它们。
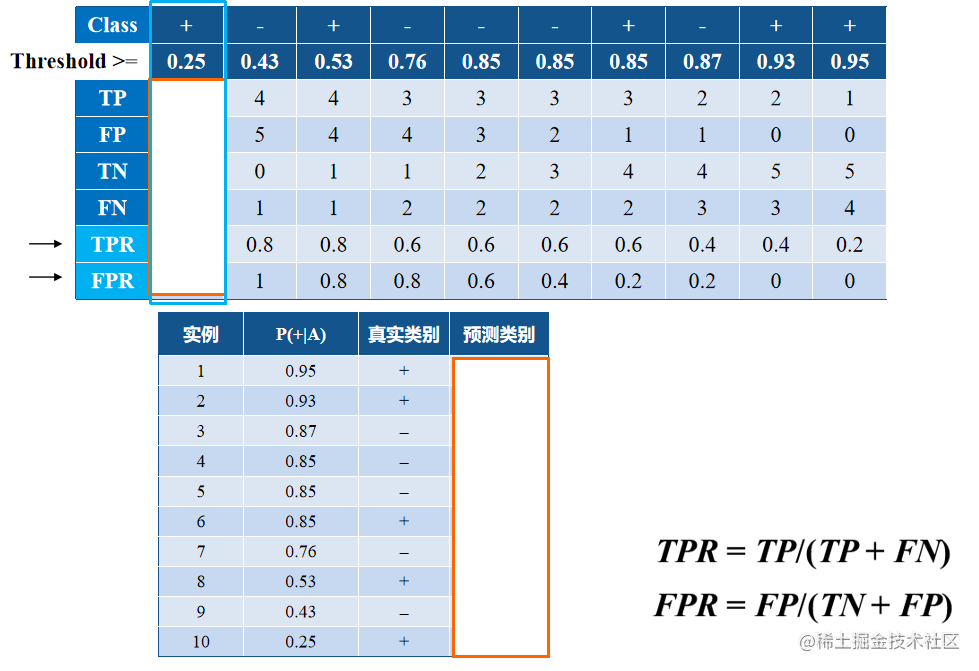
将折线图按照连接凸点忽略凹点的方式去画出弧线图.
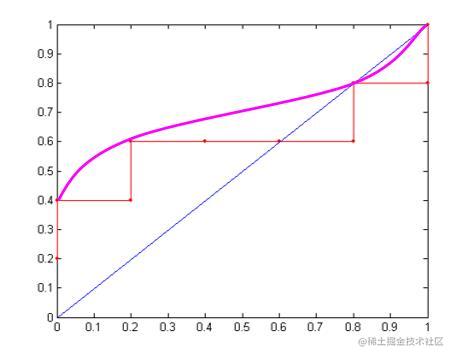
- ROC曲线越靠近左上角,模型的准确性越高。
ROC曲线的缺点: - 如果根据ROC曲线对分类器模型进行比较时,两个分类器模型的ROC曲线发生交叉,则难以断言两者孰优孰劣。
解决办法——AUC: - AUC即ROC曲线下与坐标轴围成的面积。用于衡量二分类模型的优劣,表示预测的正例排在负例前面的概率。
- AUC取值一般在【0.5,1】之间,等于1表示准确性最高,等于0.5则没有应用价值。








![解决Dockerfile错误: ERROR [3/3] RUN yum install -y wget vim net-tools](https://img-blog.csdnimg.cn/645686d83bac4537b1bcf7c40f2dac7d.png)