从0实现基于Alpha zero的中国象棋AI

0.0、前言

​ 题主对于阿尔法狗的实现原理好奇，加上毕业在即，因此选择中国象棋版的阿尔法zero，阿尔法zero是阿尔法狗的升级版。在完成代码编写的历程中，深刻感受到深度学习环境的恶劣，网络上固然资料繁多，但要么水平不行，不知所云，要么国外课程，门槛过高。因而碰壁良多，才想着自己写一篇博文，完整详细的阐述作为普通人的我以及大家如何去一步步实现中国象棋AI。

​ 同时，预先说明：题主认为学习深度学习一定要有目标，如完成一个垃圾检测等等，具体落实到项目，以完成项目为驱动力，无关知识了解即可，切勿系统学习，贪多。深度学习庞大而深奥，一个小方向就足以研究一生。

​ 总体而言，想要基于python编写阿尔法zero需要使用到如下知识：

• 熟悉python语法
• 知道如何使用pytorch完成卷积神经网络与残差神经网络
• 会使用Anaconda创建虚拟环境

默认读者有以上三者基础，没有也无所吊谓，只是无法敲出代码，理论才是最重要的。

​ 阿尔法zero算法主要由两部分组成：残差神经网络与蒙特卡洛树搜索。这二者也是下面会详细阐述的内容，同时会扩展到卷积神经网络与原生蒙特卡洛树搜索。

0.1、阿尔法狗 和 阿尔法 zero区别

阿尔法狗：需要预先收集大量棋局信息制作成数据集，对神经网络进行训练，然后在人机对弈时会结合神经网络的输出与蒙特卡洛树搜索进行落子

阿尔法zero：无需事先准备棋局数据，通过自我对弈，在对弈过程中收集棋局信息，然后将信息制作成数据集对神经网络进行训练，在自我对弈与人机对弈中同样使用神经网络与蒙特卡洛树搜索进行落子

很显然，对于普通人来讲，不需要额外数据的阿尔法zero更适合

1.0、原生蒙特卡洛树搜索

​ 鉴于阿尔法zero所需知识过多，若直接概览全局，反而不知所云。因此题主边提出问题边讲解，让读者知道为啥要这样做，而不是这样做就行了。

1.1、穷举法

​ 我们以最简单的井字棋为例，在一个空白的棋盘上选择哪一步落子为当前方最优捏？

​ 最简单的方法就是穷举、如红方落在左上角位置，黑方落在旁边，一直交替落子最终分出胜负，然后棋局回归到红方落子在左上角位置，此时黑方再选择不同地方落子，再次交替落子，再次分出胜负。直到黑方无未重复落子位置，则记录模拟次数以及这些次数中红胜利的次数形成，红落子在左上角的胜率，仿照上述行为，模拟出空棋盘下红方所有可以落子的行动以及行动对应的胜率，最终选择胜率最大的作为真实落子。

​ 可以看到，上述方法确实是有用的，但缺点也很明显，需要庞大的算力支持，如果将游戏改为象棋或者围棋，是不可能支撑如此庞大的运算。

​ 因此，我们需要一种算法，能够减少计算量，使其更加高效。

​ 蒙特卡洛树搜索应运而生。

1.2、原生蒙特卡洛树搜索

​ 原生的蒙特卡洛树搜索会从开始到随机策略，逐渐过渡到有一定选择性的策略。具体如下：

​ 原生蒙特卡洛树搜索有四步骤：选择，扩展，模拟，反向传播、

​ 先大致讲一下原生蒙特卡洛树搜索：

​ 通过算法选择输入局面的所有可能落子中一个，生成子节点（子节点被选择次数加一，总搜索次数加一），以子节点开始模拟红黑方交替落子，直至分出胜负，若红胜且子节点为红方落子，则子节点价值设置为1，然后重新以初始局面选择所有落子可能中一个，且某些动作已生成子节点且存在价值，则计算此动作的最终值需加入此节点价值进行计算。然后重复以上步骤，最终输出被选择次数多的落子动作为真实落子。

​ 再详细讲解（以井字棋为例）：

1、初始局面为3X3的空棋盘。创建全局变量all_count：记录总搜索次数，输入此局面下应该为哪一方落子，这里默认红方

初始化一颗树的数据结构（后续以 A 表示此初始节点与棋盘），树中存储：

• a_count=0（表示此节点被选中次数，但是初始节点用不到，后面节点才用得到）
• 一个二维数组，表示空棋盘
• value：表示此节点价值（初始节点用不到）
• play：表示是红方还是黑方（初始节点用不到）

2、计算此局面下红方所有可能都落子动作，很显然有9种。

3、使用 上置信界算法 计算每一种落子动作的最终价值（此价值与节点中存储的价值不是一个东西），并选择值最大的动作生成子节点**(扩展**)

---------------------------------------------------------------------------------上置信界算法---------------------------------------------------------------------------------------

上置信界算法：

​ 核心：兼顾探索与价值。

​ 解释：在此棋局中，若一味使用价值最大的作为子节点，会照成每次都选择相同节点，因初始时价值都为0，一旦选择一个子节点且价值大于0后，后续就只会选择此节点，若有其他落子潜在价值大于此也不会被选中，因此需要一种算法，让搜索次数增加的同时，选中次数小的动作其被选中的概率增加。只要符合算法思想，怎样设计算法都没问题，这里提供一个简单的：

UCB(上置信界) = value + c X 总搜索次数 / 节点被选中次数 + 1 (这里是为了方便理解，所以化繁为简，真实的算法可以适当更改以更贴合)

value：节点价值，c：偏置，就是一个自定义的常数，用来平衡探索与价值的

---------------------------------------------------------------------------------回到步骤---------------------------------------------------------------------------------------------

​ 由算法可知、当前局面下的 UCB 全部一样，都是 0，因为此时没有子节点生成，所有 9 种动作都没有价值 且都没有被选择，总次数也为 0 。所以我们还是会依据算法选择一个动作进行扩展，比如说是左上角第一个，这里无关紧要因为并非最终落子。

​ 选择左上角第一个后，总次数加一，创建子节点 B ，且其父节点为初始节点，子节点被选中次数加一，即：

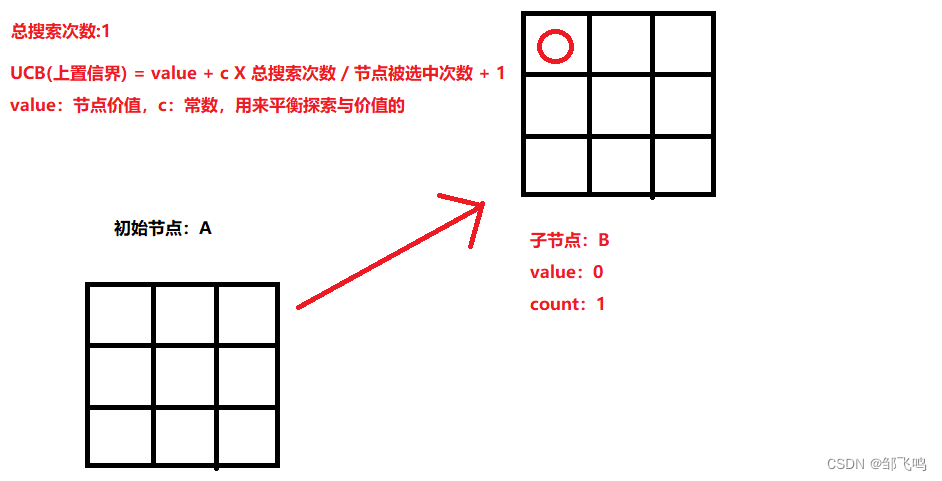
4、模拟

​ 我们以子节点B为起始，模拟红黑双方交替落子，直至分出胜负。

​ 注意，交替落子不会生成子节点，且完全随机。（因为模拟的落子是没有 价值 这个变量，所以只能随机）若最终胜方与此子节点落子方一致则value变为1，反之变为-1

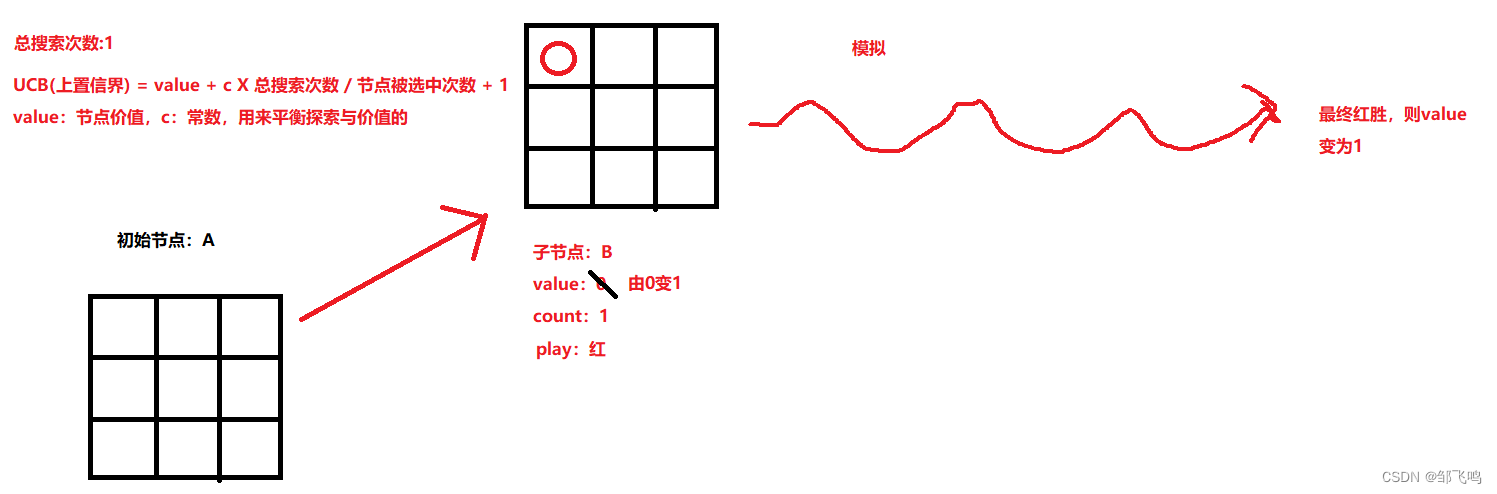
5、反向传播：就是上述value变为1了，由于只进行一次搜索只有一个子节点，且树深度为2，所以不能完全体现反向传播，后面会再讲。

6、此时才算进行完一次搜索，接下来进行第二次搜索，（注：总搜索次数增加应该是在搜索完成时增加，节点被访问次数是在节点被访问或者创建时增加）

7、同样以初始空棋盘为起点，再次计算上置信界值（常数我们设置为2，这里是为了方便演示所以尽量减少探索，注重价值），计算可知：因此，我们再次选择第一排第一个作为

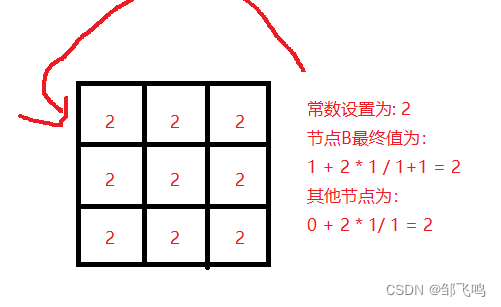
8、由于选择的是已经存在的节点，因此我们不进行扩展，而是以此节点局面再次计算此节点局面下所有可能落子动作的UCB值，注意此时就是应该黑方落子了，所以是求黑方所有可能落子。由此局面可知，黑方有 8 种落子方式。我们分别求取这八种方式的 UCB 值，并选择落子动作进行扩展，同样这八种的UCB全为 2 （即此局面下不存在任何一个子节点，因此也就不存在价值），因此，我们选哪一个都可以，这里选第一排第二个，此时局面变为：

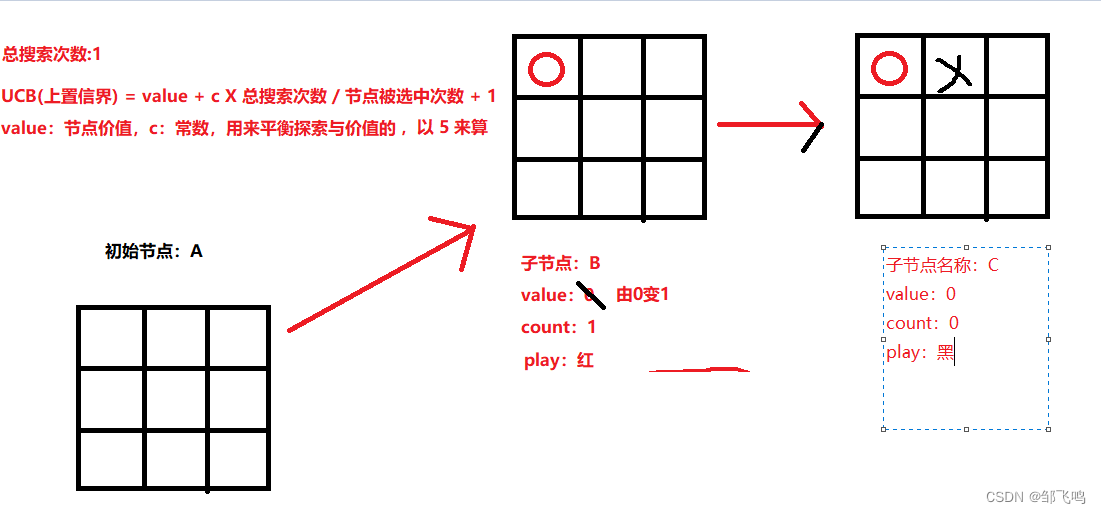
9、再次以 C 节点的局面作为模拟初始局面，此时若模拟结果是黑赢，那么此局面最终价值应该为：1

10、反向传播：我们通过模拟知道了C节点价值，此时需要将价值回传，即通过子节点寻找父节点，又因为父节点是另一方落子，所以父节点更新后价值应该为：（父节点原价值 - 子节点价值）/ 2。也就是B节点更新后价值

由于B节点的父节点为初始节点，所以不需要再将价值传递给初始节点了。

同时，总搜索次数加一，即all_count = 2，至于节点被访问次数，则是按照关系链来进行增加，比如上述节点C次数需要加一，其父节点B在反向传播时也需要加一。所以最终结果如下：

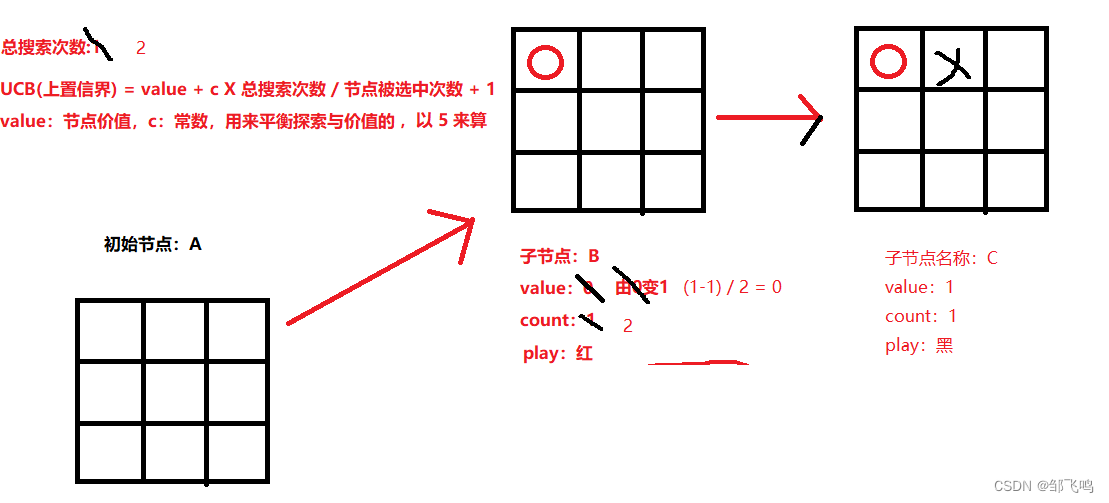
11、此时我们再次计算初始局面（空棋盘）时个落子动作的UCB值：

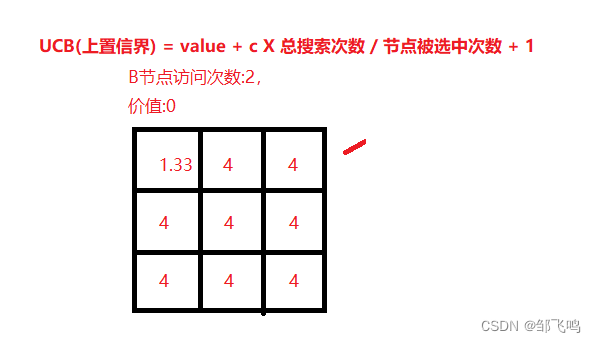
由图可知，我们可取第一排第二个作为节点 D 进行扩展：

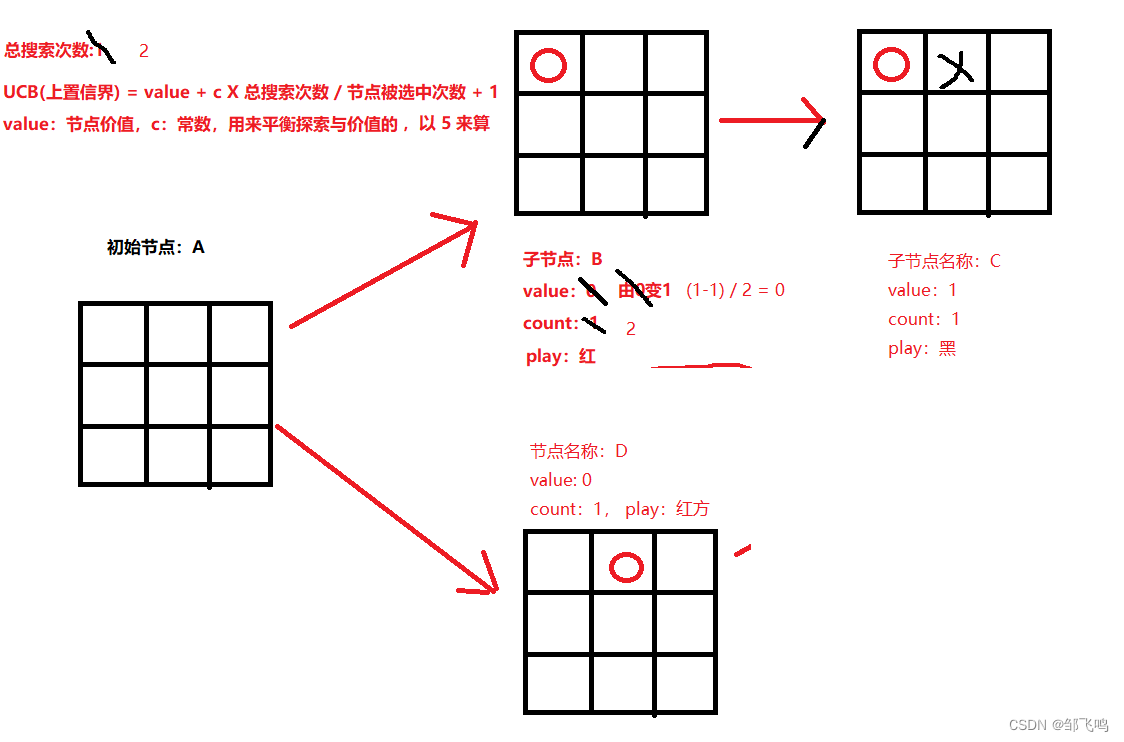
12、然后就是继续模拟，反向传播，然后再次从初始节点开始进行新一轮搜索，如此循环往复直到到达指定搜索次数。

13、最终，我们会选择初始节点下的子节点中被访问次数最大的作为蒙特卡洛树搜索的输出，如上图中，子节点有 2 个，且B节点次数大于D节点，因此我们选择B节点作为输出，也就是第一排第一个的动作。

总结：

优点：

​ 纵观全部原生蒙特卡洛树搜索，最关键处就是上置信界算法和模拟这两者去抉择最优解。它比穷举法更加高效，通过算法可以不需要全部遍历完就能选择出相对优解。同时又保留了一部分穷举的特点，模拟操作可以真实知道对应动作的价值，并且在后续选择中由开始的注重探索过渡到注重价值。

缺点：

​ 经过上述过程可以看出，虽然能够节省大部分时间，但是我们每一次搜索的模拟步骤中必须要到达终局，这对于大型棋类游戏而言还是不太适合，还是需要算力，因此，基于残差神经网络的蒙特卡洛树搜索应运而生。

1.3、基于残差神经网络的蒙特卡洛树搜索

在原蒙特卡洛树搜索基础上增加了两个东西，策略与价值。

也就是原来的 上置信界算法 算法被修改为：

上述讲解value值时还要细节没提到，等下会详细讲。

先说说残差神经网络的输出，一般神经网络只输出只有一个，但是为啥需要两个输出呢？

正常情况其实我们只需要价值输出即可，即value值，在模拟时用到，但是这里还加了一个概率输出。

说实话，有用，但是具体为啥一定需要就找不到很有说服力的依据。

再说说策略输出到底输出的是啥？

若将空棋盘输入到残差神经网络。因为刚开始红方有9种可能落子，所以策略网络最终会输出每一个可能动作被选择的概率，如下：

其和应该是1，这里只是示例，随便设置了几个数值。

策略输出相当于神经网络对当前局面的预判，它认为某些落子动作更有价值，就会提高对应概率，这样在计算此局面所有动作的UCB值时加入，可提高对应动作的值，使最优解能够更明显，这也是为啥我说有用的地方。

价值网络输出：就是输出一个值，这个值可以当做当前局面的价值来看（可以看作当前局面对于落子方的有利程度）。但是一般我们不直接将此局面的价值设置为此节点价值。而是通过模拟这个步骤获得节点最终价值。

模拟步骤会与原生蒙特卡洛树搜索不同！

原生蒙特卡洛树搜索一定是要达到终究，无论双方交替落子多少次，但是基于残差神经网络的蒙特卡洛树搜索由于残差神经网络可以输出每个局面的价值，即每次交替落子的局面价值，这样存储每个局面价值，然后交替落子一定步骤后，即使未到达终局也可以使用反向传播的方式求取平均价值作为此子节点价值。当然，在指定次数中若出现终局则价值以终局价值为准。

总结：基于残差神经网络的蒙特卡洛树搜索，有两方面提示：

1、神经网络会输出每个动作的概率，这样可以更加准确找到最优解，因为概率越大最终值越大。

2、由于神经网络还可以输出某个局面价值，使用我们在模拟步骤时，不需要一定到达终局就能够获得价值。

且随着神经网络训练次数的增加，概率与价值的值会越贴近正确值。如上，也是为何需要残差神经网络辅助的原因。