1.2.2 基于最小势能原理的线性有限元一般格式

现在市场上的有限元分析软件普遍都是基于位移法进行求解的，其数学原理就是上节的最小势能原理变分提法。回顾上节推导过程，首先需要根据位移条件确定可能位移的范围，其次根据假设的可能位移代入几何方程和本构方程，得到基于位移的应力应变的表达式，最后代入$\delta II=0$的方程求解相关待定参数。线性有限元求解的一般格式基本上也是一样的，除此之外线性有限元会多一些其他步骤，比如结构的离散化、位移模式假定等。下图为线性有限元求解的一般格式。
（加图）

1.2.2.1 离散化

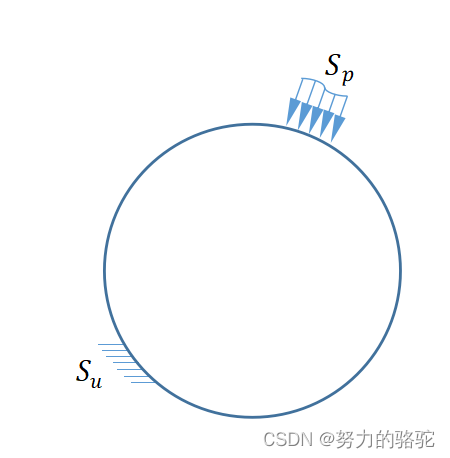
将结构进行离散化建模，是有限元分析工作中的第一步，某典型的结构如下图所示，其中结构为一个圆盘，将其离散成若干四边形网格单元，如下图所示。结构离散化合适与否一定程度上决定使用有限元分析方法解决工程问题的精度。

1.2.2.2 位移插值

（a）位移模式
在最小势能原理中首先需要根据位移条件确定可能位移的范围，但是在通常的分析中，我们为了方便处理，往往将可能位移用多项式来逼近，这个过程就是单元的位移模式选择。
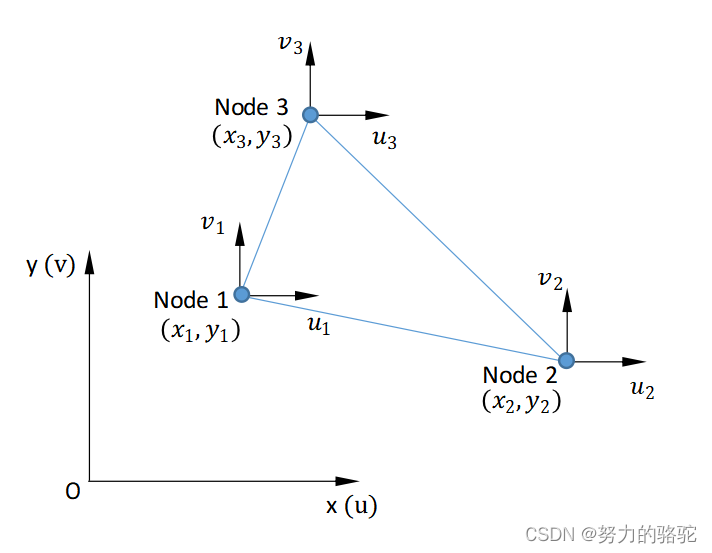
我们以一阶二维三角形单元为例，二维三角形单元有6各位移自由度。用多项式拟合可能位移，如下式所示

$$\begin{array}{r}u(x,y)={\overline{a}}_0+{\overline{a}}_{1}x+{\overline{a}}_{2}y\\ v(x,y)={\overline{b}}_0+{\overline{b}}_{1}x+{\overline{b}}_{2}y\end{array}\text{\hspace{1em}(1-54)}$$

（b）形函数
多项式位移模式有六个待定参数，二维三角形单元有六个节点位移变量，所以六个待定参数可以表示成六个节点位移变量的形式，如下式，待定系数满足下式。
$$\begin{array}{r}\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\right]=\left[\begin{array}{ccc}1& x_1& y_1\\ 1& x_2& y_2\\ 1& x_3& y_3\end{array}\right]\left[\begin{array}{c}{\overline{a}}_0\\ {\overline{a}}_1\\ {\overline{a}}_2\end{array}\right],\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\end{array}\right]=\left[\begin{array}{ccc}1& x_1& y_1\\ 1& x_2& y_2\\ 1& x_3& y_3\end{array}\right]\left[\begin{array}{c}{\overline{b}}_0\\ {\overline{b}}_1\\ {\overline{b}}_2\end{array}\right]\end{array}\text{\hspace{1em}(1-55)}$$
那么系数为
$$\begin{array}{r}\left[\begin{array}{c}{\overline{a}}_0\\ {\overline{a}}_1\\ {\overline{a}}_2\end{array}\right]={\left[\begin{array}{ccc}1& x_1& y_1\\ 1& x_2& y_2\\ 1& x_3& y_3\end{array}\right]}^{-1}\left[\begin{array}{c}{u}_1\\ u_2\\ u_3\end{array}\right],\left[\begin{array}{c}{\overline{b}}_0\\ {\overline{b}}_1\\ {\overline{b}}_2\end{array}\right]={\left[\begin{array}{ccc}1& x_1& y_1\\ 1& x_2& y_2\\ 1& x_3& y_3\end{array}\right]}^{-1}\left[\begin{array}{c}{v}_1\\ v_2\\ v_3\end{array}\right]\end{array}\text{\hspace{1em}(1-56)}$$
其中逆矩阵的求解如下
$${\left[\begin{array}{ccc}1& x_1& y_1\\ 1& x_2& y_2\\ 1& x_3& y_3\end{array}\right]}^{-1}=\frac{[M_{ij}\cdot (-1{)}^{i+j}{]}^T}{A}\text{\hspace{1em}(1-57)}$$
其中$M_{ij}$为原矩阵的余子式，典型如下，其乘上$(-1{)}^{i+j}$称为代数余子式，矩阵的逆是其代数余子式组成的伴随矩阵除以该矩阵的行列式。

经过求解，系数矩阵的逆矩阵如下式
$$\begin{array}{rl}{\left[\begin{array}{ccc}1& x_1& y_1\\ 1& x_2& y_2\\ 1& x_3& y_3\end{array}\right]}^{-1}& ={\left|\begin{array}{ccc}1& x_1& y_1\\ 1& x_2& y_2\\ 1& x_3& y_3\end{array}\right|}^{-1}\cdot \left[\begin{array}{ccc}\left|\begin{array}{cc}{x}_2& y_2\\ x_3& y_3\end{array}\right|& -\left|\begin{array}{cc}{x}_1& y_1\\ x_3& y_3\end{array}\right|& \left|\begin{array}{cc}{x}_1& y_1\\ x_2& y_2\end{array}\right|\\ & & \\ -\left|\begin{array}{cc}1& y_2\\ 1& y_3\end{array}\right|& \left|\begin{array}{cc}1& y_1\\ 1& y_3\end{array}\right|& -\left|\begin{array}{cc}1& y_1\\ 1& y_2\end{array}\right|\\ & & \\ \left|\begin{array}{cc}1& x_2\\ 1& x_3\end{array}\right|& -\left|\begin{array}{cc}1& x_1\\ 1& x_3\end{array}\right|& \left|\begin{array}{cc}1& x_1\\ 1& x_2\end{array}\right|\end{array}\right]\\ =\frac{1}{A}\left[\begin{array}{ccc}{a}_1& a_2& a_3\\ b_1& b_2& b_3\\ c_1& c_2& c_3\end{array}\right]& \end{array}\text{\hspace{1em}(1-58)}$$
那么，系数可以表达成
$$\begin{array}{r}{\overline{a}}_0=\frac{1}{A}(a_1{u}_1+a_2{u}_2+a_3{u}_3)\\ {\overline{a}}_1=\frac{1}{A}(b_1{u}_1+b_2{u}_2+b_3{u}_3)\\ {\overline{a}}_2=\frac{1}{A}(c_1{u}_1+c_2{u}_2+c_3{u}_3)\end{array}\text{\hspace{1em}(1-59)}$$
上式代入位移模式，可得
$$\begin{array}{rl}u(x,y)& ={\overline{a}}_0+{\overline{a}}_{1}x+{\overline{a}}_{2}y\\ & =\frac{1}{A}(a_1{u}_1+a_2{u}_2+a_3{u}_3)+\frac{1}{A}(b_1{u}_1+b_2{u}_2+b_3{u}_3)x+\frac{1}{A}(c_1{u}_1+c_2{u}_2+c_3{u}_3)y\\ & =\frac{1}{A}(a_1+b_{1}x+c_{1}y)u_1+\frac{1}{A}(a_2+b_{2}x+c_{2}y)u_2+\frac{1}{A}(a_3+b_{3}x+c_{3}y)u_3\\ & =N_1(x,y)u_1+N_2(x,y)u_2+N_3(x,y)u_3\end{array}\text{\hspace{1em}(1-60)}$$
同理，可得
$$\begin{array}{rl}v(x,y)& ={\overline{a}}_0+{\overline{a}}_{1}x+{\overline{a}}_{2}y\\ & =\frac{1}{A}(a_1{v}_1+a_2{v}_2+a_3{v}_3)+\frac{1}{A}(b_1{v}_1+b_2{v}_2+b_3{v}_3)x+\frac{1}{A}(c_1{v}_1+c_2{v}_2+c_3{v}_3)y\\ & =\frac{1}{A}(a_1+b_{1}x+c_{1}y)v_1+\frac{1}{A}(a_2+b_{2}x+c_{2}y)v_2+\frac{1}{A}(a_3+b_{3}x+c_{3}y)v_3\\ & =N_1(x,y)v_1+N_2(x,y)v_2+N_3(x,y)v_3\end{array}\text{\hspace{1em}(1-61)}$$
可以将二维三角形单元内任意一点的位移写成矩阵的形式，如下
$$\begin{array}{rl}\mathbf{u}(x,y)=\left[\begin{array}{c}u(x,y)\\ v(x,y)\end{array}\right]& =\left[\begin{array}{cccccc}{N}_1(x,y)& 0& N_2(x,y)& 0& N_3(x,y)& 0\\ 0& N_1(x,y)& 0& N_2(x,y)& 0& N_3(x,y)\end{array}\right]\left[\begin{array}{c}{u}_1\\ v_1\\ u_2\\ v_2\\ u_3\\ v_3\end{array}\right]\\ & =\mathbf{N}(x,y)\cdot {\mathbf{q}}^e\end{array}\text{\hspace{1em}(1-62)}$$
我们称$\mathbf{N}(x,y)$为形状函数矩阵，而 ${\mathbf{q}}^e$为单元的节点位移列阵。形状函数矩阵作用 就是用节点位移列阵插值得到任意一点位移的插值函数。

1.2.2.3 单元应变

应变和位移的关系由几何方程确定，在本文二维的例子中，应变仅有三个分量，那么应变与位移的关系可以如下式所示。
$$\begin{array}{rl}\mathbf{\epsilon }(x,y)=\left[\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\gamma }_{xy}\end{array}\right]=\left[\begin{array}{c}\frac{\partial u}{\partial x}\\ \frac{\partial v}{\partial y}\\ \frac{\partial u}{\partial y}+\frac{\partial v}{\partial x}\end{array}\right]& =\left[\begin{array}{cc}\frac{\partial }{\partial x}& 0\\ 0& \frac{\partial }{\partial y}\\ \frac{\partial }{\partial y}& \frac{\partial }{\partial x}\end{array}\right]\cdot \left[\begin{array}{c}u(x,y)\\ v(x,y)\end{array}\right]\\ & =\left[\begin{array}{cc}\frac{\partial }{\partial x}& 0\\ 0& \frac{\partial }{\partial y}\\ \frac{\partial }{\partial y}& \frac{\partial }{\partial x}\end{array}\right]\cdot \mathbf{N}(x,y)\cdot {\mathbf{q}}^e\\ & =\mathbf{B}(x,y)\cdot {\mathbf{q}}^e\end{array}\text{\hspace{1em}(1-63)}$$

1.2.2.4 单元应力

应力应变关系又成本构方程，在线性范围内，应力与应变的关系写成矩阵如下(本例中为二维三角形单元，应力分量只有三个)
$$\begin{array}{rl}\mathbf{\sigma }(x,y)=\left[\begin{array}{c}{\sigma }_{xx}\\ {\sigma }_{yy}\\ {\tau }_{xy}\end{array}\right]& =\frac{E}{1-{\mu }^2}\left[\begin{array}{ccc}1& \mu & 0\\ \mu & 1& 0\\ 0& 0& \frac{1-\mu }{2}\end{array}\right]\left[\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\gamma }_{xy}\end{array}\right]\\ & =\mathbf{D}(x,y)\cdot \mathbf{\epsilon }(x,y)\\ & =\mathbf{D}(x,y)\cdot \mathbf{B}(x,y)\cdot {\mathbf{q}}^e\\ & =\mathbf{S}(x,y)\cdot {\mathbf{q}}^e\end{array}\text{\hspace{1em}(1-64)}$$

1.2.2.5 单元刚度矩阵

回顾物体的总势能表达式，并将其写成矩阵的形式
$$\begin{array}{rl}II& =\frac{1}{2}{\int }_{\Omega }{\sigma }_{ij}{\epsilon }_{ij}d\Omega -{\int }_{\Omega }{b}_i{u}_{i}d\Omega -{\int }_A{p}_i{u}_{i}dA\\ & =\frac{1}{2}{\int }_{\Omega }{\mathbf{\sigma }}^T\mathbf{\epsilon }\mathbf{d}\Omega -{\int }_{\Omega }{\mathbf{b}}^T\mathbf{ud}\Omega -{\int }_A{\mathbf{p}}^T\mathbf{ud}A\end{array}\text{\hspace{1em}(1-65)}$$
将前述单元的应力、应变矩阵等代入上式，建立单元的总势能表达式，如下所示

$$\begin{array}{rl}II& =\frac{1}{2}{\int }_{\Omega }{\mathbf{\sigma }}^T\mathbf{\epsilon }\mathbf{d}\Omega -{\int }_{\Omega }{\mathbf{b}}^T\mathbf{ud}\Omega -{\int }_A{\mathbf{p}}^T\mathbf{ud}A\\ & =\frac{1}{2}{\int }_{\Omega }{{\mathbf{q}}^{\mathbf{e}}}^T{\mathbf{B}}^{\mathbf{T}}{\mathbf{D}}^{\mathbf{T}}\mathbf{B}{\mathbf{q}}^{\mathbf{e}}\mathbf{d}\Omega -{\int }_{\Omega }{\mathbf{b}}^T\mathbf{N}{\mathbf{q}}^{\mathbf{e}}\mathbf{d}\Omega -{\int }_A{\mathbf{p}}^T\mathbf{N}{\mathbf{q}}^{\mathbf{e}}\mathbf{d}A\\ & =\frac{1}{2}{{\mathbf{q}}^{\mathbf{e}}}^T({\int }_{\Omega }{\mathbf{B}}^{\mathbf{T}}{\mathbf{D}}^{\mathbf{T}}\mathbf{Bd}\Omega ){\mathbf{q}}^{\mathbf{e}}-({\int }_{\Omega }{\mathbf{b}}^T\mathbf{Nd}\Omega +{\int }_A{\mathbf{p}}^T\mathbf{Nd}A){\mathbf{q}}^{\mathbf{e}}\\ & =\frac{1}{2}{{\mathbf{q}}^{\mathbf{e}}}^T{\mathbf{K}}^{\mathbf{e}}{\mathbf{q}}^{\mathbf{e}}-{{\mathbf{P}}^{\mathbf{e}}}^T{\mathbf{q}}^{\mathbf{e}}\end{array}\text{\hspace{1em}(1-66)}$$
回顾之前最小势能原理，真实位移是使得势能取得最小值，上式是单元的总势能，那么真实的位移使得势能取到最小值，也就是说总势能一阶变分为零，即
$$\delta II=\frac{\partial II}{\partial q^e}\delta q^e=({\mathbf{K}}^{\mathbf{e}}{\mathbf{q}}^{\mathbf{e}}-{\mathbf{P}}^{\mathbf{e}})\delta q^e=0\text{\hspace{1em}(1-67)}$$
由于$\delta q^e$的任意性，可以得到
$${\mathbf{K}}^{\mathbf{e}}{\mathbf{q}}^{\mathbf{e}}-{\mathbf{P}}^{\mathbf{e}}=0\text{\hspace{1em}(1-68)}$$
其中${\mathbf{K}}^{\mathbf{e}}$为单元刚度矩阵（由上式中的量纲分析，${\mathbf{K}}^{\mathbf{e}}$为刚度的量纲），${\mathbf{P}}^{\mathbf{e}}$为节点等效载荷。

1.2.2.6 整体刚度矩阵

对于物体来说，一般有多个单元，那么就可以建立多个单元平衡方程，如下所示
$${\mathbf{K}}_{(\mathbf{i})}^{\mathbf{e}}{\mathbf{q}}_{(\mathbf{i})}^{\mathbf{e}}-{\mathbf{P}}_{(\mathbf{i})}^{\mathbf{e}}=0\text{\hspace{1em}(1-69)}$$
按照顺序将所有的单元的节点位移组成总体节点位移列阵，相应的节点等效载荷和单元刚度矩阵组成总体节点等效载荷列阵和整体刚度矩阵，以下图为例，下图总共有两个单元，得到两个单元平衡方程
$$\begin{array}{r}\left[\begin{array}{cccccc}{k}_{11}^1& k_{12}^1& k_{13}^1& k_{14}^1& k_{15}^1& k_{16}^1\\ k_{21}^1& k_{22}^1& k_{23}^1& k_{24}^1& k_{25}^1& k_{26}^1\\ k_{31}^1& k_{32}^1& k_{33}^1& k_{34}^1& k_{35}^1& k_{36}^1\\ k_{41}^1& k_{42}^1& k_{43}^1& k_{44}^1& k_{45}^1& k_{46}^1\\ k_{51}^1& k_{52}^1& k_{53}^1& k_{54}^1& k_{55}^1& k_{56}^1\\ k_{61}^1& k_{62}^1& k_{63}^1& k_{64}^1& k_{65}^1& k_{66}^1\end{array}\right]\left[\begin{array}{c}{u}_1\\ v_1\\ u_2\\ v_2\\ u_3\\ v_3\end{array}\right]=\left[\begin{array}{c}{p}_{x1}^1\\ p_{y1}^1\\ p_{x2}^1\\ p_{y2}^1\\ p_{x3}^1\\ p_{y3}^1\end{array}\right]\\ \left[\begin{array}{cccccc}{k}_{11}^2& k_{12}^2& k_{13}^2& k_{14}^2& k_{15}^2& k_{16}^2\\ k_{21}^2& k_{22}^2& k_{23}^2& k_{24}^2& k_{25}^2& k_{26}^2\\ k_{31}^2& k_{32}^2& k_{33}^2& k_{34}^2& k_{35}^2& k_{36}^2\\ k_{41}^2& k_{42}^2& k_{43}^2& k_{44}^2& k_{45}^2& k_{46}^2\\ k_{51}^2& k_{52}^2& k_{53}^2& k_{54}^2& k_{55}^2& k_{56}^2\\ k_{61}^2& k_{62}^2& k_{63}^2& k_{64}^2& k_{65}^2& k_{66}^2\end{array}\right]\left[\begin{array}{c}{u}_2\\ v_2\\ u_3\\ v_3\\ u_4\\ v_4\end{array}\right]=\left[\begin{array}{c}{p}_{x2}^2\\ p_{y2}^2\\ p_{x3}^2\\ p_{y3}^2\\ p_{x4}^2\\ p_{y4}^2\end{array}\right]\end{array}\text{\hspace{1em}(1-70)}$$
叠加整理后，整体平衡方程为
$$\left[\begin{array}{cccccccc}{k}_{11}^1& k_{12}^1& k_{13}^1& k_{14}^1& k_{15}^1& k_{16}^1& 0& 0\\ k_{21}^1& k_{22}^1& k_{23}^1& k_{24}^1& k_{25}^1& k_{26}^1& 0& 0\\ k_{31}^1& k_{32}^1& k_{33}^1+k_{11}^2& k_{34}^1+k_{12}^2& k_{35}^1+k_{13}^2& k_{36}^1+k_{14}^2& k_{15}^2& k_{16}^2\\ k_{41}^1& k_{42}^1& k_{43}^1+k_{21}^2& k_{44}^1+k_{22}^2& k_{45}^1+k_{23}^2& k_{46}^1+k_{24}^2& k_{25}^2& k_{26}^2\\ k_{51}^1& k_{52}^1& k_{53}^1+k_{31}^2& k_{54}^1+k_{32}^2& k_{55}^1+k_{33}^2& k_{56}^1+k_{34}^2& k_{35}^2& k_{36}^2\\ k_{61}^1& k_{62}^1& k_{63}^1+k_{41}^2& k_{64}^1+k_{42}^2& k_{65}^1+k_{43}^2& k_{66}^1+k_{44}^2& k_{45}^2& k_{46}^2\\ 0& 0& k_{51}^2& k_{52}^2& k_{53}^2& k_{54}^2& k_{55}^2& k_{56}^2\\ 0& 0& k_{61}^2& k_{62}^2& k_{63}^2& k_{64}^2& k_{65}^2& k_{66}^2\end{array}\right]\left[\begin{array}{c}{u}_1\\ v_1\\ u_2\\ v_2\\ u_3\\ v_3\\ u_4\\ v_4\end{array}\right]=\left[\begin{array}{c}{p}_{x1}^1\\ p_{y1}^1\\ p_{x2}^1+p_{x2}^2\\ p_{y2}^1+p_{y2}^2\\ p_{x3}^1+p_{x3}^2\\ p_{y3}^1+p_{y3}^2\\ p_{x4}^2\\ p_{y4}^2\end{array}\right]\text{\hspace{1em}(1-71)}$$

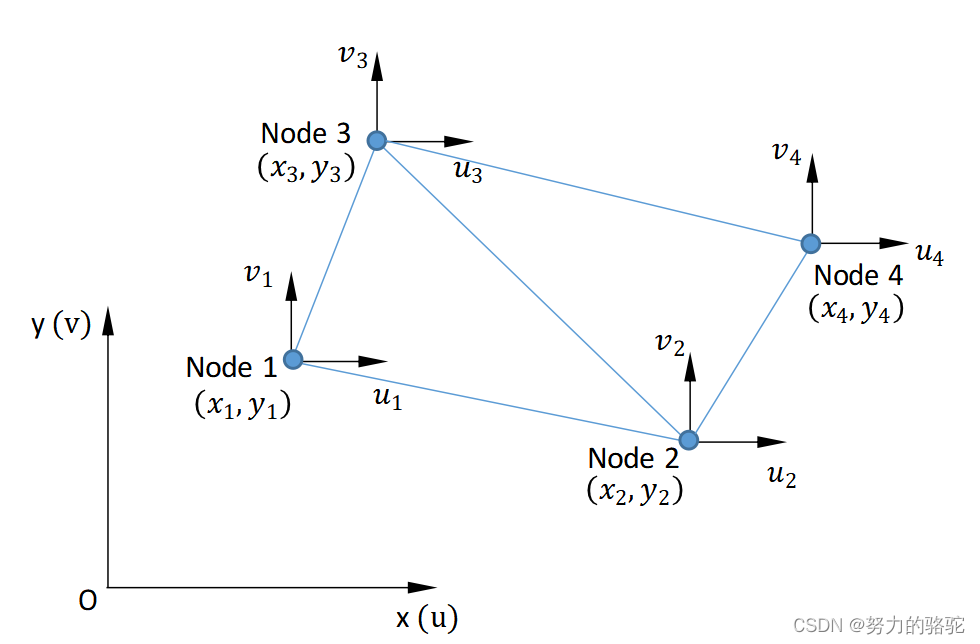
1.2.2.7 处理约束

如果在上例中，假设节点1为约束，那么$u_1=v_1=0$，上式变为
$$\left[\begin{array}{cccccccc}{k}_{11}^1& k_{12}^1& k_{13}^1& k_{14}^1& k_{15}^1& k_{16}^1& 0& 0\\ k_{21}^1& k_{22}^1& k_{23}^1& k_{24}^1& k_{25}^1& k_{26}^1& 0& 0\\ k_{31}^1& k_{32}^1& k_{33}^1+k_{11}^2& k_{34}^1+k_{12}^2& k_{35}^1+k_{13}^2& k_{36}^1+k_{14}^2& k_{15}^2& k_{16}^2\\ k_{41}^1& k_{42}^1& k_{43}^1+k_{21}^2& k_{44}^1+k_{22}^2& k_{45}^1+k_{23}^2& k_{46}^1+k_{24}^2& k_{25}^2& k_{26}^2\\ k_{51}^1& k_{52}^1& k_{53}^1+k_{31}^2& k_{54}^1+k_{32}^2& k_{55}^1+k_{33}^2& k_{56}^1+k_{34}^2& k_{35}^2& k_{36}^2\\ k_{61}^1& k_{62}^1& k_{63}^1+k_{41}^2& k_{64}^1+k_{42}^2& k_{65}^1+k_{43}^2& k_{66}^1+k_{44}^2& k_{45}^2& k_{46}^2\\ 0& 0& k_{51}^2& k_{52}^2& k_{53}^2& k_{54}^2& k_{55}^2& k_{56}^2\\ 0& 0& k_{61}^2& k_{62}^2& k_{63}^2& k_{64}^2& k_{65}^2& k_{66}^2\end{array}\right]\left[\begin{array}{c}0\\ 0\\ u_2\\ v_2\\ u_3\\ v_3\\ u_4\\ v_4\end{array}\right]=\left[\begin{array}{c}{R}_{x1}\\ R_{y1}\\ p_{x2}^1+p_{x2}^2\\ p_{y2}^1+p_{y2}^2\\ p_{x3}^1+p_{x3}^2\\ p_{y3}^1+p_{y3}^2\\ p_{x4}^2\\ p_{y4}^2\end{array}\right]\text{\hspace{1em}(1-72)}$$
其中$R_{x1}、R_{y1}$为支反力，将上式化为两个方程
$$\begin{array}{rl}\left[\begin{array}{cccccc}{k}_{33}^1+k_{11}^2& k_{34}^1+k_{12}^2& k_{35}^1+k_{13}^2& k_{36}^1+k_{14}^2& k_{15}^2& k_{16}^2\\ k_{43}^1+k_{21}^2& k_{44}^1+k_{22}^2& k_{45}^1+k_{23}^2& k_{46}^1+k_{24}^2& k_{25}^2& k_{26}^2\\ k_{53}^1+k_{31}^2& k_{54}^1+k_{32}^2& k_{55}^1+k_{33}^2& k_{56}^1+k_{34}^2& k_{35}^2& k_{36}^2\\ k_{63}^1+k_{41}^2& k_{64}^1+k_{42}^2& k_{65}^1+k_{43}^2& k_{66}^1+k_{44}^2& k_{45}^2& k_{46}^2\\ k_{51}^2& k_{52}^2& k_{53}^2& k_{54}^2& k_{55}^2& k_{56}^2\\ k_{61}^2& k_{62}^2& k_{63}^2& k_{64}^2& k_{65}^2& k_{66}^2\end{array}\right]\left[\begin{array}{c}{u}_2\\ v_2\\ u_3\\ v_3\\ u_4\\ v_4\end{array}\right]& =\left[\begin{array}{c}{p}_{x2}^1+p_{x2}^2\\ p_{y2}^1+p_{y2}^2\\ p_{x3}^1+p_{x3}^2\\ p_{y3}^1+p_{y3}^2\\ p_{x4}^2\\ p_{y4}^2\end{array}\right]\\ \overline{K}{\overline{q}}^e& =\overline{P}\end{array}\text{\hspace{1em}(1-73)}$$

$$\left[\begin{array}{cccc}{k}_{13}^1& k_{14}^1& k_{15}^1& k_{16}^1\\ k_{23}^1& k_{24}^1& k_{25}^1& k_{26}^1\end{array}\right]\left[\begin{array}{c}{u}_2\\ v_2\\ u_3\\ v_3\end{array}\right]=\left[\begin{array}{c}{R}_{x1}\\ R_{y1}\end{array}\right]\text{\hspace{1em}(1-74)}$$

1.2.2.8 求解节点载荷列阵

1.2.2.9 求解位移列阵

最终通过上式求得位移列阵${\overline{q}}^e={\overline{K}}^{-1}\cdot \overline{P}$，再将与$[u_1,v_1{]}^T=[0,0{]}^T$组装成最终的节点位移列阵${\mathbf{q}}^{\mathbf{e}}$。

1.2.2.10 计算应力矩阵等

计算得到最终的节点位移列阵${\mathbf{q}}^{\mathbf{e}}$后通过一系列的回代得到单元内任意位置的位移、应变、应力矩阵，而式（1-74）用来求解约束支反力。
$$\begin{array}{r}\mathbf{u}(x,y)=\mathbf{N}(x,y)\cdot {\mathbf{q}}^e\\ \mathbf{\epsilon }(x,y)=\mathbf{B}(x,y)\cdot {\mathbf{q}}^e\\ \mathbf{\sigma }(x,y)=\mathbf{S}(x,y)\cdot {\mathbf{q}}^e\end{array}\text{\hspace{1em}(1-75)}$$