F. Editorial for Two（二分答案+反悔贪心）

F. Editorial for Two

1、问题

给定一个$n$和$k$，以及一个长度为$n$数组。现在从$n$个数中，挑出$k$个数，称作个子序列。然后将这个子序列分成两部分，记作子序列1和子序列2。那么子序列1和子序列2都有一个对应的和。这两个和能够比较出一个最大值。现在我们要求的是最大值的最小值。

2、分析

这里有一个很常用的套路，当题目中让我们求最大值的最小值或者最小值的最大值的时候，一般采用二分来解决。

我们这里二分最终的答案。

对于二分而言，难点在于$check$函数的书写。

这道题中，$check$函数的作用是判断二分过程中的$mid$值是否合理。

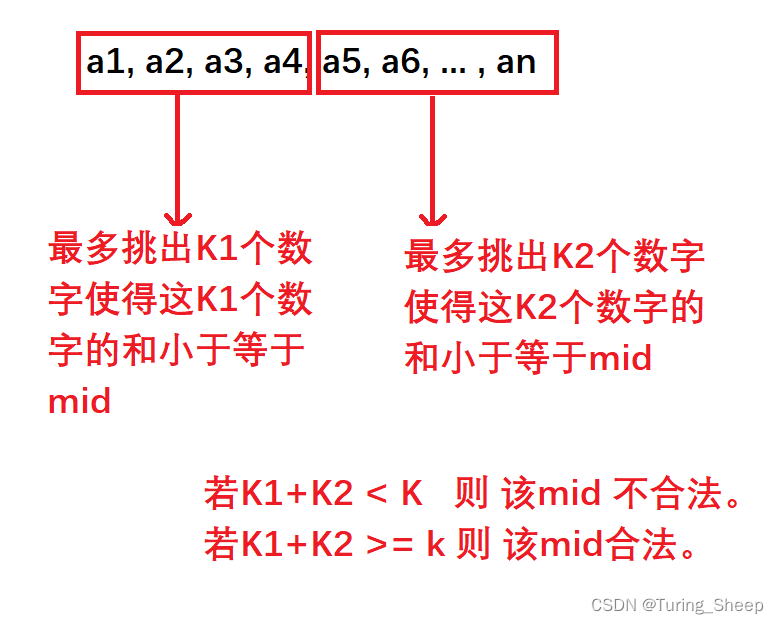
那么这个挑出最多$k1$个数的过程，用到了反悔贪心，反悔贪心的思路就是当所选数字的和小于$mid$的时候，就尽可能多的选数字，当大于$mid$的时候，就删除选择数字中的最大值，目的是留出更大空间选择更多的数字，而这个选择最大值的过程可以用大根堆来优化。

除此以外，图中前缀后缀划分的位置是不确定的，所以我们需要枚举所有的划分位置，找到一个可行的方案。

因此，我们可以先利用反悔贪心先预处理出来所有的前缀后缀中最多选择的数字$k1,k2$。然后再枚举划分位置，判断是否存在一组$k1+k2\ge k$。

3、代码

#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;


bool check(int maxv, int n, vector<int>a, int k)
{
	vector<int>f(n + 1, 0), g(n + 1, 0);
	priority_queue<int>q, qq;
	int sum = 0;
	for(int i = 0; i < n; i ++)
	{
		if(sum + a[i] <= maxv)
		{
			sum += a[i];
			q.push(a[i]);
			f[i + 1] = f[i] + 1;
		}
		else
		{
			q.push(a[i]);
			sum += a[i];
			sum -= q.top();
			q.pop();
			f[i + 1] = f[i];
		}
	}
	sum = 0;
	reverse(a.begin(), a.end());
	for(int i = 0; i < n; i ++)
	{
		if(sum + a[i] <= maxv)
		{
			sum += a[i];
			qq.push(a[i]);
			g[i + 1] = g[i] + 1;
		}
		else
		{
			sum += a[i];
			qq.push(a[i]);
			sum -= qq.top();
			qq.pop();
			g[i + 1] = g[i]; 
		}
	}

	for(int i = 1; i <= n; i ++ )
	{
		if(f[i] + g[n - i] >= k)
			return true;			
	}
	return false;

}

void solve()
{
	int n, k;
	cin >> n >> k;
	vector<int>a(n);
	int sum = 0;
	for(int i = 0; i < n; i ++)
	{
		cin >> a[i];
		sum += a[i];
	}
	int l = 0, r = sum;
	while(l < r)
	{
		int mid = l + r >> 1;
		if(check(mid, n, a, k))
			r = mid;
		else
			l = mid + 1;
	}
	cout << l << endl;
}

signed main()
{
	ios::sync_with_stdio(0);
	cin.tie(0);
	cout.tie(0);
	int t;
	cin >> t;
	while(t--)
	solve();
}