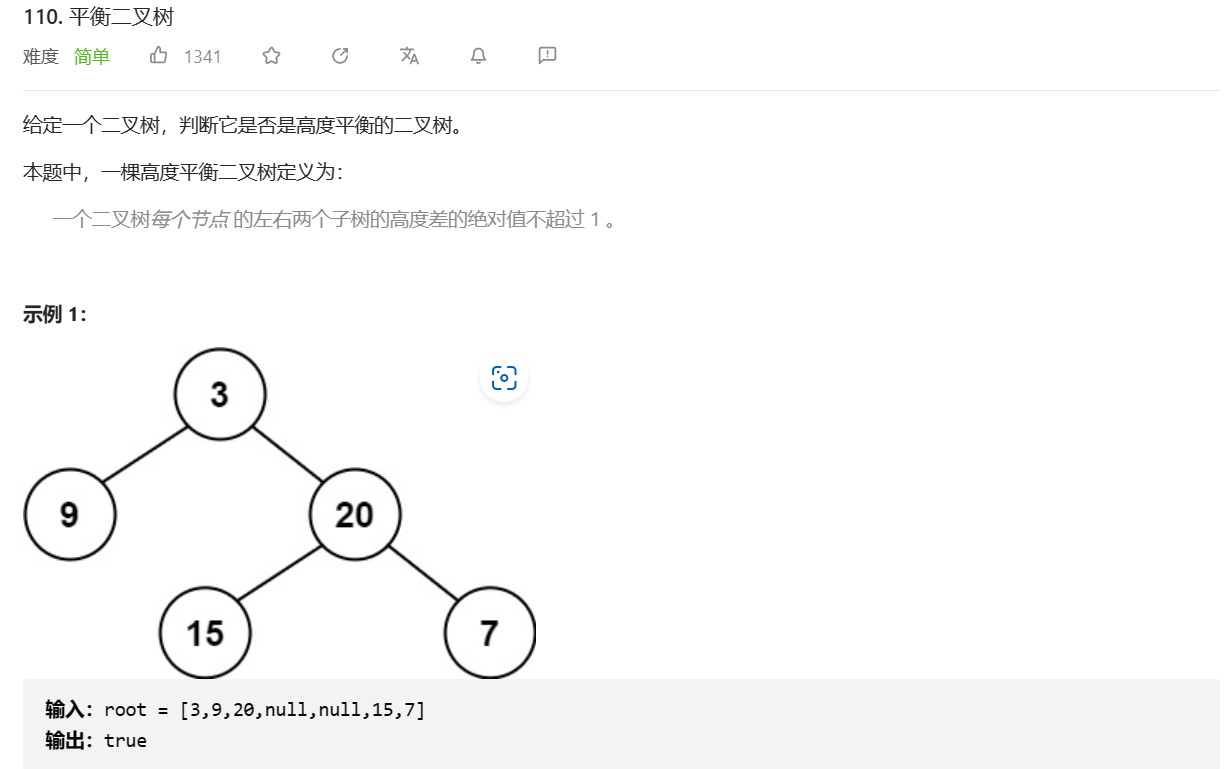
1. 递归法求解

递归三部曲：

• 确定递归函数的参数及其返回值
• 确定终止条件
• 确定单层递归逻辑

深度：从上往下
高度：从下往上

1.1 根据深度求解

• 构建求二叉树节点深度的函数（后序遍历）
• 递归求该树是否是平衡二叉树（前序遍历）
  • 递归函数的参数只需要当前节点 TreeNode* cur，返回值为 bool
  • 终止条件：当前节点为空，则直接返回 true
  • 单层递归逻辑：（1）判断当前节点（2）判断左子树（3）判断右子树

  int lDepth = getDepth(root->left);
  int rDepth = getDepth(root->right);
  if(abs(lDepth - rDepth) > 1){				//判断中间节点是否满足条件
      return false;
  }
  bool lflag = isBalanced(root->left);		//判断左子树是否满足条件
  bool rflag = isBalanced(root->right);		//判断右子树是否满足条件
  return lflag && rflag;
  

int getDepth(TreeNode* node){
   if(node == NULL)
       return 0;
   return 1 + max(getDepth(node->left), getDepth(node->right));
}

bool isBalanced(TreeNode* root) {
   if(root == NULL)
       return true;
   int lDepth = getDepth(root->left);
   int rDepth = getDepth(root->right);
   if(abs(lDepth - rDepth) > 1){
       return false;
   }
   return isBalanced(root->left) && isBalanced(root->right);
}

1.2 根据高度求解（后序遍历）

• 递归求高度
  • 递归函数的参数只需要当前节点 TreeNode* node，返回值为以该节点为根节点树的高度

  //-1表示已经不是平衡二叉树了，否则返回值为以该节点为根节点树的高度
  int getHeight(TreeNode* node)
  

  • 终止条件：当前节点为空，直接返回0
  • 单层递归逻辑

  int lHeight = getHeight(node->left);					//左
  if(lHeight == -1)	return -1;
  int rHeight = getHeight(node->right);					//右
  if(rHeight == -1)	return -1;
  
  int result;
  if(abs(lHeight - rHeight) > 1)							//中
  	result = -1;
  else
  	result = 1 + max(lHeight, rHeight);					//以当前节点为根节点的树的最大高度
  return result;
  

// 返回以该节点为根节点的二叉树的高度，如果不是平衡二叉树了则返回-1
int getHeight(TreeNode* node) {
    if (node == NULL) {
        return 0;
    }
    int leftHeight = getHeight(node->left);
    if (leftHeight == -1) return -1;
    int rightHeight = getHeight(node->right);
    if (rightHeight == -1) return -1;
    return abs(leftHeight - rightHeight) > 1 ? -1 : 1 + max(leftHeight, rightHeight);
}
bool isBalanced(TreeNode* root) {
    return getHeight(root) == -1 ? false : true;
}