B树(C语言描述)

news2024/11/28 14:42:37

一.概念

B树是一种多路平衡查找树，不同于二叉平衡树，他不只是有两个分支，而是有多个分支，一棵m阶B树(balanced tree of order m)是一棵平衡的m路搜索树，B树用于磁盘寻址，它是一种高效的查找算法。

二.性质

  • 根节点至少有2个子女
  • 每个非根节点所包含的关键字个数x满足以下关系：⌈m/2⌉−1⩽x⩽m−1\lceil m/2 \rceil - 1 \leqslant x \leqslant m - 1⌈m/2⌉−1⩽x⩽m−1
  • 所有叶子结点都在同一层
  • 除根结点以外的所有结点（不包括叶子结点）的度数正好是关键字总数加1，故内部子树个数 k 满足：⌈m/2⌉⩽k⩽m\lceil m/2 \rceil \leqslant k \leqslant m⌈m/2⌉⩽k⩽m

三.B树的各种操作 

1.B树的插入 

B树的插入操作只能在叶子结点上进行操作，而且叶子结点上关键字的个数要严格满足B树的性质：⌈m/2⌉−1⩽x⩽m−1\lceil m/2 \rceil - 1 \leqslant x \leqslant m - 1⌈m/2⌉−1⩽x⩽m−1

插入步骤如下：

  1. 寻找合适的叶子结点
  2. 在叶子结点上找到合适的插入位置
  3. 插入后判断关键字个数是否超过m-1，如果超过则结点需要分裂，分裂从中间劈开，并将中间的元素插入到当前结点的父亲结点中，判断父亲结点关键字个数是否超过m-1，如果超过继续分裂，重复第3步

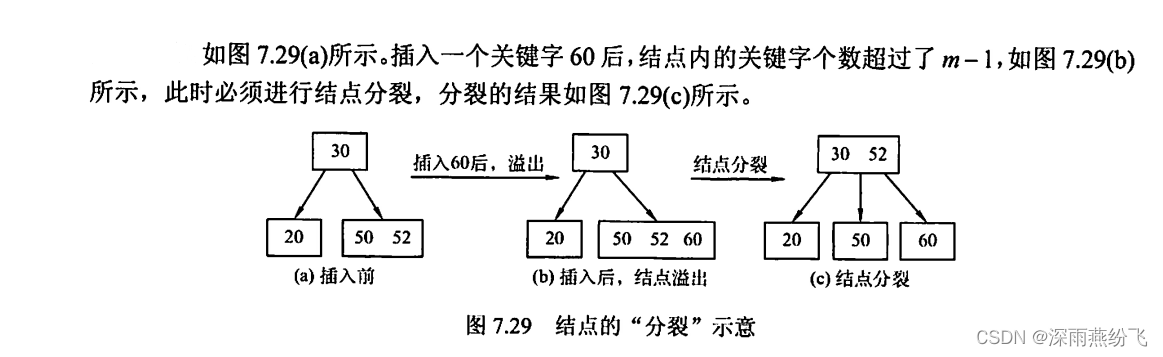
 2.B树的删除

 

 

 

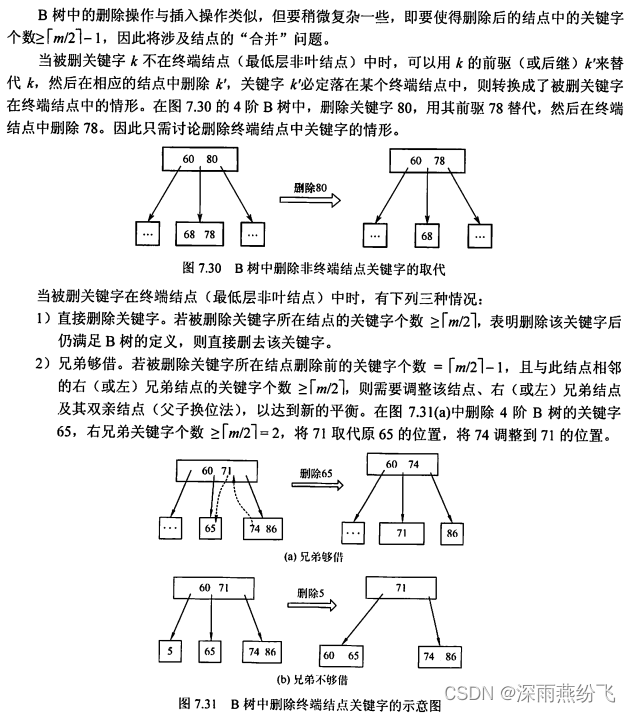
 四.代码各函数分解实例

1.结点的结构体定义 

typedef struct Node
{
	int level;//阶数 
	int keyNum;//关键数的数量
	int childNum;//孩子的数量
	int *keys;//关键字指针数组
	struct Node **children;//孩子数组
	struct Node *parent;//父亲指针 
}Node;

 2.初始化结点

Node *initNode(int level)
{/*参数:树的阶数*/
	Node *node = (Node*)malloc(sizeof(Node));//申请结点的空间 
	node->level = level;//将阶数写入 
	node->keyNum = 0;//关键字个数初始为0 
	node->childNum = 0;//孩子个数初始为0 
	/*level+1是为了后面的插入和删除,方便索引*/
	node->keys = (int*)malloc(sizeof(int)*(level+1));//结点内关键字指针申请空间 
	node->children = (Node**)malloc(sizeof(Node*)*level);//孩子指针申请空间 
	node->parent = NULL;//父结点初始为空 
	int i;
	for(i=0;i<level;i++)
	{/*关键字和孩子指针循环遍历都初始化*/
		node->keys[i] = 0;
		node->children[i] = NULL;
	}
	node->keys[i] = 0;//关键字指针多一个,因此额外初始化 
	return node;//指针函数,返回值为指针 
}

 3.找合适的索引方便插入和删除

int findSuiteIndex(Node *node,int data)
{/*参数一:结点指针
参数二:要查找的元素*/
	int index;//下标 
	for(index=1;index<=node->keyNum;index++)
	{/*从1开始,向后遍历寻找第一个比该元素大的key,返回该key的下标,就是要插入的位置*/
		if(data<node->keys[index])
			break;
	}
	return index;
}

 4.找合适的叶子结点

Node *findSuiteLeafNode(Node *T,int data)
{/*参数一:根节点指针
参数二:要插入的元素*/
	int index;//元素下标 
	if(T->childNum==0)//结点无孩子说明找到了叶子结点 
		return T;
	else
	{
		index = findSuiteIndex(T,data);//寻找合适的插入位置 
		return findSuiteLeafNode(T->children[index-1],data);//递归,往左子树走 
	}
}

 5.往结点中插入数据

void addData(Node *node,int data,Node **T)
{/*参数一:结点指针
参数二:要插入的数据
参数三:父结点,由于要改变,因此使用二级指针*/
	int index = findSuiteIndex(node,data);
	int i,mid;
	for(i=node->keyNum;i>=index;i--)
		node->keys[i+1] = node->keys[i];
	node->keys[index] = data;
	node->keyNum += 1;
	//判断是否进行分裂 
	if(node->keyNum==node->level)
	{//找到分裂的位置 
		mid = node->level/2+node->level%2;
		//分裂 
		Node *lchild = initNode(node->level);//初始化左孩子结点 
		Node *rchild = initNode(node->level);//初始化右孩子结点
		//将mid左边的值赋值给左孩子 
		for(i=1;i<mid;i++)
			addData(lchild,node->keys[i],T);
		//将mid右边的值赋值给右孩子 
		for(i=mid+1;i<=node->keyNum;i++)
			addData(rchild,node->keys[i],T);
		//将原先结点mid左边的孩子赋值给分裂出来的左孩子 
		for(i=0;i<mid;i++)
		{
			lchild->children[i] = node->children[i];
			if(node->children[i]!=NULL)
			{
				node->children[i]->parent = lchild;
				lchild->childNum++;
			}
		}
		//将原先结点mid右边的孩子赋值给分裂出来的右孩子 
		int index = 0;
		for(i=mid;i<node->childNum;i++)
		{
			rchild->children[index++] = node->children[i];
			if(node->children[i]!=NULL)
			{
				node->children[i]->parent = rchild;
				rchild->childNum++;
			}
		}
		//判断当前结点是不是根结点 
		if(node->parent==NULL)
		{//是根结点 
			Node *newParent = initNode(node->level);
			addData(newParent,node->keys[mid],T);
			newParent->children[0] = lchild;
			newParent->children[1] = rchild;
			newParent->childNum = 2;
			lchild->parent = newParent;
			rchild->parent = newParent;
			*T = newParent;
		}
		else
		{//不是根结点 
			index = findSuiteIndex(node->parent,node->keys[mid]);
			lchild->parent = node->parent;
			rchild->parent = node->parent;
			node->parent->children[index-1] = lchild;
			if(node->parent->children[index]!=NULL)
			{
				for(i=node->parent->childNum-1;i>=index;i--)
					node->parent->children[i+1] = node->parent->children[i];
			}
			node->parent->children[index] = rchild;
			node->parent->childNum++;
			addData(node->parent,node->keys[mid],T);
		}
	}
}

 6.插入结点

void insert(Node** T, int data) 
{/*参数一:父结点
参数二:要插入的数据*/
    Node* node = findSuiteLeafNode(*T, data);//先找到适合插入的叶子结点 
    addData(node, data, T);//执行插入数据函数 
}

 7.遍历输出

void printTree(Node* T) 
{/*参数:根结点*/
	int i;
    if (T != NULL) {
        for (i  = 1; i <= T -> keyNum; i++)//按序遍历结点内的关键字 
            printf("%d ", T -> keys[i]);
        printf("\n");

        for (i = 0; i < T -> childNum; i++)//按序遍历孩子结点 
            printTree(T -> children[i]);//递归遍历 
    }
}

 8.主函数

int main()
{
	int i;
	Node *T = initNode(5);//初始化 
	for(i=1;i<=10;i++)
		insert(&T,i);//插入 
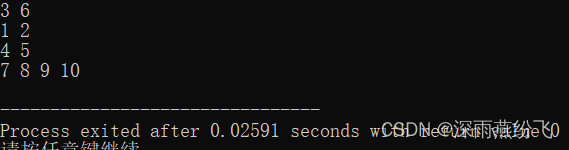
	printTree(T);//遍历打印 
	return 0;
}

 完整代码:

#include <stdio.h>
#include <stdlib.h>
typedef struct Node
{
	int level;//阶数 
	int keyNum;//关键数的数量
	int childNum;//孩子的数量
	int *keys;//关键字指针数组
	struct Node **children;//孩子数组
	struct Node *parent;//父亲指针 
}Node;
/*初始化结点*/
Node *initNode(int level)
{/*参数:树的阶数*/
	Node *node = (Node*)malloc(sizeof(Node));//申请结点的空间 
	node->level = level;//将阶数写入 
	node->keyNum = 0;//关键字个数初始为0 
	node->childNum = 0;//孩子个数初始为0 
	/*level+1是为了后面的插入和删除,方便索引*/
	node->keys = (int*)malloc(sizeof(int)*(level+1));//结点内关键字指针申请空间 
	node->children = (Node**)malloc(sizeof(Node*)*level);//孩子指针申请空间 
	node->parent = NULL;//父结点初始为空 
	int i;
	for(i=0;i<level;i++)
	{/*关键字和孩子指针循环遍历都初始化*/
		node->keys[i] = 0;
		node->children[i] = NULL;
	}
	node->keys[i] = 0;//关键字指针多一个,因此额外初始化 
	return node;//指针函数,返回值为指针 
}
/*找合适的索引方便插入和删除*/
int findSuiteIndex(Node *node,int data)
{/*参数一:结点指针
参数二:要查找的元素*/
	int index;//下标 
	for(index=1;index<=node->keyNum;index++)
	{/*从1开始,向后遍历寻找第一个比该元素大的key,返回该key的下标,就是要插入的位置*/
		if(data<node->keys[index])
			break;
	}
	return index;
}
/*找合适的叶子结点*/
Node *findSuiteLeafNode(Node *T,int data)
{/*参数一:根节点指针
参数二:要插入的元素*/
	int index;//元素下标 
	if(T->childNum==0)//结点无孩子说明找到了叶子结点 
		return T;
	else
	{
		index = findSuiteIndex(T,data);//寻找合适的插入位置 
		return findSuiteLeafNode(T->children[index-1],data);//递归,往左子树走 
	}
}
/*往结点中插入数据*/
void addData(Node *node,int data,Node **T)
{/*参数一:结点指针
参数二:要插入的数据
参数三:父结点,由于要改变,因此使用二级指针*/
	int index = findSuiteIndex(node,data);
	int i,mid;
	for(i=node->keyNum;i>=index;i--)
		node->keys[i+1] = node->keys[i];
	node->keys[index] = data;
	node->keyNum += 1;
	//判断是否进行分裂 
	if(node->keyNum==node->level)
	{//找到分裂的位置 
		mid = node->level/2+node->level%2;
		//分裂 
		Node *lchild = initNode(node->level);//初始化左孩子结点 
		Node *rchild = initNode(node->level);//初始化右孩子结点
		//将mid左边的值赋值给左孩子 
		for(i=1;i<mid;i++)
			addData(lchild,node->keys[i],T);
		//将mid右边的值赋值给右孩子 
		for(i=mid+1;i<=node->keyNum;i++)
			addData(rchild,node->keys[i],T);
		//将原先结点mid左边的孩子赋值给分裂出来的左孩子 
		for(i=0;i<mid;i++)
		{
			lchild->children[i] = node->children[i];
			if(node->children[i]!=NULL)
			{
				node->children[i]->parent = lchild;
				lchild->childNum++;
			}
		}
		//将原先结点mid右边的孩子赋值给分裂出来的右孩子 
		int index = 0;
		for(i=mid;i<node->childNum;i++)
		{
			rchild->children[index++] = node->children[i];
			if(node->children[i]!=NULL)
			{
				node->children[i]->parent = rchild;
				rchild->childNum++;
			}
		}
		//判断当前结点是不是根结点 
		if(node->parent==NULL)
		{//是根结点 
			Node *newParent = initNode(node->level);
			addData(newParent,node->keys[mid],T);
			newParent->children[0] = lchild;
			newParent->children[1] = rchild;
			newParent->childNum = 2;
			lchild->parent = newParent;
			rchild->parent = newParent;
			*T = newParent;
		}
		else
		{//不是根结点 
			index = findSuiteIndex(node->parent,node->keys[mid]);
			lchild->parent = node->parent;
			rchild->parent = node->parent;
			node->parent->children[index-1] = lchild;
			if(node->parent->children[index]!=NULL)
			{
				for(i=node->parent->childNum-1;i>=index;i--)
					node->parent->children[i+1] = node->parent->children[i];
			}
			node->parent->children[index] = rchild;
			node->parent->childNum++;
			addData(node->parent,node->keys[mid],T);
		}
	}
}
/*插入结点*/
void insert(Node** T, int data) 
{/*参数一:父结点
参数二:要插入的数据*/
    Node* node = findSuiteLeafNode(*T, data);//先找到适合插入的叶子结点 
    addData(node, data, T);//执行插入数据函数 
}
/*遍历输出*/
void printTree(Node* T) 
{/*参数:根结点*/
	int i;
    if (T != NULL) {
        for (i  = 1; i <= T -> keyNum; i++)//按序遍历结点内的关键字 
            printf("%d ", T -> keys[i]);
        printf("\n");

        for (i = 0; i < T -> childNum; i++)//按序遍历孩子结点 
            printTree(T -> children[i]);//递归遍历 
    }
} 
int main()
{
	int i;
	Node *T = initNode(5);//初始化 
	for(i=1;i<=10;i++)
		insert(&T,i);//插入 
	printTree(T);//遍历打印 
	return 0;
}

 运行结果:

 

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/597782.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

【Kubernetes 入门实战课】Day03——容器的本质

【Kubernetes 入门实战课】Day03——容器的本质

系列文章目录 【Kubernetes 入门实战课】Day01——虚拟机创建及安装 【Kubernetes 入门实战课】Day02——初识容器 文章目录 系列文章目录前言一、容器到底是什么&#xff1f;二、为什么要隔离三、与虚拟机的区别是什么四、隔离是怎么实现的 前言 上一节中我们完成了在Linux虚…
阅读更多...
Anaconda下载安装及使用方法汇总

Anaconda下载安装及使用方法汇总

软件说明: Anaconda是Red Hat Linux和Fedora的安装管理程式。它以Python及C语言写成&#xff0c;以图形的PyGTK和文字的python-newt介面写成。它可以用来自动安装配置&#xff0c;使用户能够以最小的监督运行。Anaconda安装管理程式应用在RHEL&#xff0c;Fedora和其他一些项目…
阅读更多...
IMX6ULL裸机篇之I2C实验-

IMX6ULL裸机篇之I2C实验-

一. I2C 实验简介 I2C实验&#xff0c;我们就来学习如何使用 I.MX6U 的 I2C 接口来驱动 AP3216C&#xff0c;读取 AP3216C 的传感器数据。 AP3216C是一个三合一的环境光传感器&#xff0c;ALSPSIRLED&#xff0c;ALS是环境光&#xff0c;PS是接近传感器&#xff0c;IR是红外L…
阅读更多...
MANTOO车联网RSU终端助您畅享智慧出行！

MANTOO车联网RSU终端助您畅享智慧出行！

一、案例背景 随着社会经济的飞速发展&#xff0c;汽车逐渐走进了千家万户&#xff0c;目前我国家庭乘用汽车保有量在2.6亿辆&#xff0c;平均每6个人就拥有一辆汽车。汽车保有量的上涨同时也给道路交通安全带来了极大的挑战&#xff0c;为了降低交通事故发生&#xff0c;保障…
阅读更多...
牛客网项目—开发社区首页

牛客网项目—开发社区首页

视频连接&#xff1a;开发社区首页_哔哩哔哩_bilibili 代码地址&#xff1a;Community: msf begin 仿牛客论坛项目 (gitee.com) 本文是对仿牛客论坛项目的学习&#xff0c;学习本文之前需要了解Java开发的常用框架&#xff0c;例如SpringBoot、Mybatis等等。如果你也在学习牛…
阅读更多...
遗传算法讲解

遗传算法讲解

遗传算法&#xff08;Genetic Algorithm&#xff0c;GA&#xff09; 是模拟生物在自然环境中的遗传和进化的过程而形成的自适应全局优化搜索算法。它借用了生物遗传学的观点&#xff0c;通过自然选择、遗传和变异等作用机制&#xff0c;实现各个个体适应性的提高。 基因型 (G…
阅读更多...
文件阅览功能的实现(适用于word、pdf、Excel、ppt、png...)

文件阅览功能的实现(适用于word、pdf、Excel、ppt、png...)

需求描述&#xff1a; 需要一个组件&#xff0c;同时能预览多种类型文件&#xff0c;一种类型文件可有多个的文件。 看过各种博主的方案&#xff0c;其中最简单的是利用第三方地址进行预览解析&#xff08;无需任何插件&#xff09;&#xff1b; 这里推荐三个地址&#xff1a…
阅读更多...
EasyExcel实现excel区域三级联动(模版下载)

EasyExcel实现excel区域三级联动(模版下载)

序号 前言需求不通过excel,实现省市区级联实战pom.xml配置controller配置service类业务处理类测试 前言 首先&#xff0c;我们先来了解一下java实现模板下载的几种方式 1、使用poi实现2、使用阿里的easyexcel实现 今天社长就给大家说一下easyexcel的实现模板下载的之旅。在这里…
阅读更多...
phpword使用整理

phpword使用整理

目录 介绍 安装 创建文档 设置默认字体和字号 设置文本样式 编号标题 换行符 分页符 超链接 创建表格 添加图片 文件保护 加载word文件 内容转化为html 保存 模板替换 格式 加载模板 替换字符串 替换图片 替换表格 总结 参考 介绍 PHPWord 是一个用纯 …
阅读更多...
Vue3 过渡动画效果

Vue3 过渡动画效果

文章目录 Vue3 过渡动画效果概述<Transition>组件简单使用为过渡效果命名自定义过渡classJavaScript动画效果元素间过渡 <transition-group>组件列表动画状态动画 Vue3 过渡动画效果 概述 Vue 提供了两个内置组件&#xff0c;可以帮助你制作基于状态变化的过渡和…
阅读更多...
中服云设备全生命周期管理系统4.0全新升级，震撼登场！

中服云设备全生命周期管理系统4.0全新升级，震撼登场！

6月2日&#xff0c;中服云设备全生命周期管理系统4.0将在中服云官方视频号线上直播震撼发布。在此次线上直播发布会上&#xff0c;中服云将详细地介绍设备全生命周期管理系统4.0版本的全新特性和创新功能。同时邀请了业内权威售前顾问、设备管理工程师和合作伙伴&#xff0c;共…
阅读更多...
降低FTP服务器速度的解决方案（Filezilla等）

降低FTP服务器速度的解决方案（Filezilla等）

我最近发现&#xff0c;尽管有70Mbps&#xff08;8.75MB / s&#xff09;的互联网连接和1Gbps&#xff08;125MB / s&#xff09;的专用服务器可以从中下载&#xff0c;但我似乎只能从FTP服务器上以大约16.8Mbps&#xff08;2.1MB / s&#xff09;的速度下载。在一个线程上。但…
阅读更多...
深入篇【Linux】学习必备：理解文件权限

深入篇【Linux】学习必备：理解文件权限

深入篇【Linux】学习必备&#xff1a;理解文件权限 Ⅰ.Linux权限的概念Ⅱ.Linux权限管理①.文件访问者的分类(访问者的身份)②.文件类型和访问权限(文件本身的事物属性)1.文件类型&#xff1a;2.基本权限: ③.文件权限值的表示方法1.字符表示方法2.八进制数值表示法 ④.文件访问…
阅读更多...
【活动回顾】Databend 数据库表达式框架设计与实现 @GOTC

【活动回顾】Databend 数据库表达式框架设计与实现 @GOTC

5月28日&#xff0c;“全球开源技术峰会 GOTC 2023 ”圆满落幕。在本次会上&#xff0c;Databend 数据库的 优化器 研发工程师 骆迪安作为嘉宾中的一员&#xff0c;在 rust 专题专区分会场进行了一次主题为《 Rust 实现的先进 SQL Parser 与高效表达式执行框架 — Databend 数…
阅读更多...
多语言跨境商城源码，出海跨境商城软件开发模式平台

多语言跨境商城源码，出海跨境商城软件开发模式平台

一、多语言跨境商城模式 多商家模式&#xff1a;容纳不同的商家 多用户模式&#xff1a;用户之社区&#xff0c;用户交互&#xff0c;分享和推广 支持扩展&#xff1a;使用现代化的技术架构和设计&#xff0c;包括支持并发访问、分布式数据存储等功能。 采用常用技术&#x…
阅读更多...
合工大Java大作业1：货物进销管理系统

合工大Java大作业1：货物进销管理系统

问题描述 编写一个Inventory.java完成以下功能&#xff08;没有学过Java文件处理之前&#xff0c;各位同学可以使用硬编码将数据放进两个Vector变量里。等学过Java文件处理之后&#xff0c;再补充数据文件读取部分&#xff09;&#xff1a; 1&#xff0e;程序首先打开并读取In…
阅读更多...
SpringMVC源码分析：SpringMVC九大组件分析（三）

SpringMVC源码分析：SpringMVC九大组件分析（三）

一、概述 SpringMVC九大组件如下图&#xff0c;我将一个个进行介绍。各个组件使用的入口DispatcherServlet.doDispatch是各个组件使用的入口&#xff0c;我们大部分代码都是从这里开始进入的。 二、MultipartResolver 下面是MultipartResolver组件具体的使用流程&#xff0c;…
阅读更多...
【UE打包apk过程遇到的报错】

【UE打包apk过程遇到的报错】

教程遇到的问题UE5 打包android提示 sdk未设置解决方案 UE5打包apk 报错 ERROR: cmd.exe failed with args :app:assembleDebug解决方案 我在打包的时候&#xff0c;日志中的报错信息如下&#xff08;每个人的报错信息可能不一样&#xff0c;根据报错日志找对应的解决方案&…
阅读更多...
扼流圈天线是如何解决RTK的误差源

扼流圈天线是如何解决RTK的误差源

扼流圈天线是一种用于GPS定位的天线&#xff0c;它将电流流过一圈线圈来产生电磁场&#xff0c;这个电磁场可以用来接收卫星信号。扼流圈天线的优势在于它可以有效地减少多径干扰和多路传播所造成的误差&#xff0c;从而提高定位精度。 对于RTK定位来说&#xff0c;扼流圈天线可…
阅读更多...
__LINE__打印出来的值与source insight不一致

__LINE__打印出来的值与source insight不一致

一个project里面有几百个文件&#xff0c;有些&#xff0c;__LINE__ 和pc上看到的值总是不一致 在这个函数前重新定义一下line
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023