目录

结构方程模型概述

结构方程模型匹配

1.协方差SEM

2.分段SEM 

---

在R语言中实现sem进行结构方程建模和路径图可视化 – 拓端tecdat

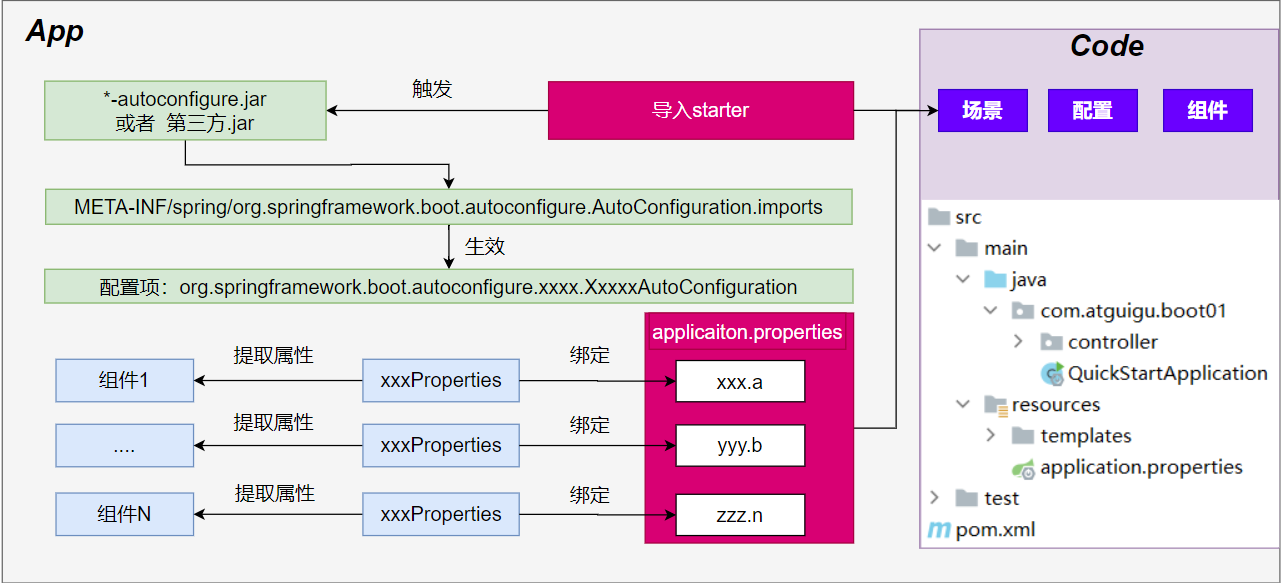
结构方程模型是一个线性模型框架，它对潜变量同时进行回归方程建模。

​​​​​​​在R语言中实现SEM进行结构方程建模和路径图可视化！

结构方程模型概述

SEM需要分析人员首先自行建立一个因子之间的关系模型，之后使用SEM对该模型进行分析，根据结果评估模型的效果，之后不断的对模型进行调整，随后重复“调整-评估”这一循环，直至结果满意为止。

首先，一点，起始模型的建立，没有统一的标准，只能由每个分析人员根据研究的实际情况自行摸索。当然也有一些前期的基本工作，比如通过一些相关性分析、VIF、CCA/RDA等筛选一下用于建模的因子，去除不必要的因子，使得起始模型的建立更简单一些，也可以通过相关性结合研究实际初步评估一下直接作用和间接作用。

第二点，对模型的调整，每个因子应该放在什么位置，因子之间的关联如何改变。常规分析两个变量间是否存在关联时，我们会使用相关性分析，但是相关性只能表明两个变量存在相互关系，但无法得出哪个变量是因？哪个变量是果？

此外，相关性分析只是两个变量数量上的相互关系，而在实际情况中，有些变量可能不是直接与其它变量发生相互作用，而是通过第三个变量间接的与靶标变量关联。

结构方程模型（Structural Equation Modeling，SEM）就是一种将两个或多个结构模型联合起来，以实现对多元关系进行建模的统计框架，其可以解决相关性分析中无法得到的因果关系以及区别直接和间接作用。

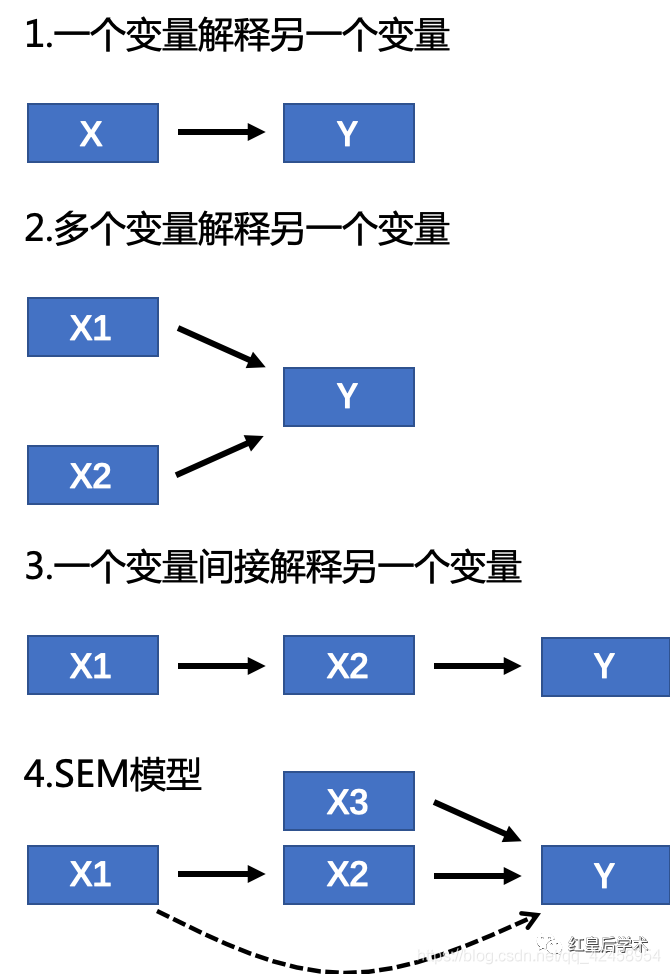
结构方程模型匹配

SEM可以分为协方差SEM和分段SEM；

1.协方差SEM

协方差SEM假定所有变量均具有正态分布，即数据服从多元正态分布，同时该分析还假定所有的变量均为独立的。

使用piecewisedSEM包的keeley数据作为示例数据，假定的初始关系为firesev由age决定，同时firesev还决定cover，使用lavaan包进行协方差SEM模型匹配。

install.packages("piecewiseSEM")
install.packages("lavaan")
library(lavaan)
library(piecewiseSEM)

data(keeley)
keeley_formula <- '
firesev ~ age
cover ~ firesev
'
keeley_sem <- sem(keeley_formula, data = keeley)

summary(keeley_sem, standardize = T, rsq = T)

lavaan 0.6-12 ended normally after 1 iterations

  Estimator                                         ML
  Optimization method                           NLMINB
  Number of model parameters                         4

  Number of observations                            90

Model Test User Model:
                                                      
  Test statistic                                 3.297
  Degrees of freedom                                 1
  P-value (Chi-square)                           0.069

Parameter Estimates:

  Standard errors                             Standard
  Information                                 Expected
  Information saturated (h1) model          Structured

Regressions:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
  firesev ~                                                             
    age               0.060    0.012    4.832    0.000    0.060    0.454
  cover ~                                                               
    firesev          -0.084    0.018   -4.611    0.000   -0.084   -0.437

Variances:
                   Estimate  Std.Err  z-value  P(>|z|)   Std.lv  Std.all
   .firesev           2.144    0.320    6.708    0.000    2.144    0.794
   .cover             0.081    0.012    6.708    0.000    0.081    0.809

R-Square:
                   Estimate
    firesev           0.206
    cover             0.191

keeley_sem <- sem(keeley_formula, data = keeley)

summary(keeley_sem, standardize = T, rsq = T)



keeley_psem <- psem(
  lm(firesev ~ age, data = keeley),
  lm(cover ~ firesev, data = keeley),
  data = keeley)
keeley_psem
fisherC(keeley_psem)
##   Fisher.C df P.Value
## 1     5.18  2   0.075
AIC(keeley_psem)
## [1] 17.18
BIC(keeley_psem)
## [1] 32.179
summary(keeley_psem, .progressBar = FALSE)

2.分段SEM 

不同于协方差SEM，分段SEM使用Fisher's C statistic代替卡方检验，但是同样要求P>0.05。AIC会在给定模型的复杂性与其拟合优度之间进行权衡，可以将AIC值视为对应了模型的准确性，AIC值越小的模型表明越有可能准确地预测新数据，AIC小于2时认为模型效果很好。

Structural Equation Model of keeley_psem 

Call:
  firesev ~ age
  cover ~ firesev

    AIC      BIC
 17.180   32.179

---
Tests of directed separation:

     Independ.Claim Test.Type DF Crit.Value P.Value 
  cover ~ age + ...      coef 87    -1.8018   0.075 

Global goodness-of-fit:

  Fisher's C = 5.18 with P-value = 0.075 and on 2 degrees of freedom

---
Coefficients:

  Response Predictor Estimate Std.Error DF Crit.Value P.Value Std.Estimate    
   firesev       age   0.0597    0.0125 88     4.7781       0       0.4539 ***
     cover   firesev  -0.0839    0.0184 88    -4.5594       0      -0.4371 ***

  Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05

---
Individual R-squared:

  Response method R.squared
   firesev   none      0.21
     cover   none      0.19

---

（于 2023-06-01 09:18:42 发布 ）