1. 相关系数

1.1 概述

相关系数是衡量两个变量之间线性相关程度的统计量。它的取值范围在-1到1之间，表示变量之间的相关性强度和方向。

1.2 Pearson相关系数

常用的相关系数有皮尔逊相关系数（Pearson correlation coefficient），它衡量的是两个连续变量之间的线性关系。皮尔逊相关系数的计算公式为：

$r(X,Y)=\frac{Cov(X,Y)}{\sigma _{x}\sigma _{y}}=\frac{E[(X-\mu _{x})(Y-\mu _{y})]}{\sigma _{x}\sigma _{y}}$ （两组数据分别减去均值后相乘）

公式中的Cov(X, Y)表示X和Y的协方差，而σ_x和σ_y分别表示X和Y的标准差，μ_x和μ_y分别表示X和Y的均值。

Pearson相关系数衡量的是两个变量之间的线性关系强度和方向。它的取值范围在-1到1之间，当相关系数r接近1时，表示变量之间存在强正相关关系；当r接近-1时，表示变量之间存在强负相关关系；当r接近0时，表示变量之间不存在线性相关关系。

示例：

X=(1,0,1） Y=(2,0,2) -> r=1

X=(1,-3,1) Y=(-2,6,-2) -> r=-1

1.3 Spearman相关系数

Spearman相关系数是一种用于衡量两个变量之间的单调关系的非参数统计指标。它与Pearson相关系数不同，不要求变量之间的关系是线性的。

公式：

$\rho _{s}=1-\frac{6\sum d_{i}^{2}}{n(n^{2}-1)}$

ρs 是Spearman相关系数
Σdᵢ² 是排序差值d的平方和的和
n 是样本大小

这个公式用于计算Spearman相关系数，它是通过排名差值的平方和来度量变量之间的单调关系。公式中的分子部分表示排序差值的平方和，分母部分则是一个归一化因子，用于调整相关系数的取值范围。

Spearman相关系数的取值范围在-1到1之间，与Pearson相关系数类似。当ρs接近1时，表示变量之间存在强正相关关系；当ρs接近-1时，表示变量之间存在强负相关关系；当ρs接近0时，表示变量之间不存在单调关系。

感谢你提供了正确的Spearman相关系数计算公式！如果还有其他问题，我会很乐意帮助你。

示例：

X=(6,11,8) Rank_X=(1,3,2)

Y=(7,4,3) Rank_Y=(3,2,1)

根据排名数据计算排名差值（d）：

d_X = (1 - 3, 3 - 2, 2 - 1) = (-2, 1, 1)
d_Y = (3 - 2, 2 - 1, 1 - 3) = (1, 1, -2)

接下来，使用Spearman相关系数的计算公式：

ρs = 1 - (6 * Σdᵢ²) / (n * (n² - 1))

其中，Σdᵢ² 表示排名差值平方和的总和，n 表示样本大小。

对于给定的数据，我们有：

Σdᵢ² = (-2)² + 1² + 1² = 6
n = 3

将这些值代入公式中，我们可以计算出Spearman相关系数：

ρs = 1 - (6 * 6) / (3 * (3² - 1)) = = 1 - (36) / (3 * (9 - 1)) = 1 - (36) / (3 * 8) = 1 - (36) / (24) = 1 - 1.5 = -0.5

因此，根据提供的数据，X和Y的Spearman相关系数为-0.5。它表明X和Y之间存在完全逆向的相关关系。

无论原始数据的绝对值大小如何变化，只要它们的排序顺序保持不变，Spearman相关系数的计算结果也会保持一致。（即使X=(9,11,8)，结果也是-0.5）

2. 线性回归

2.1 概述

回归：确定两种或两种以上变量间互相依赖的定量关系的一种统计分析方法。

线性回归是一种统计模型，用于建立自变量（预测变量）与因变量（目标变量）之间的线性关系。它假设自变量和因变量之间存在一个线性关系，并尝试通过拟合一条直线来预测因变量的值。

2.2 公式

$\hat{b}=\frac{\sum_{i=1}^{n}(x_{i}-\bar{x})(y_{i}-\bar{y})}{\sum_{i=1}^{n}(x_{i}-\bar{x})^{2}}=\frac{\sum_{i=1}^{n}x_{i}y_{i}-n\bar{x}\bar{y}}{\sum_{i=1}^{n}x_{i}^{2}-n\bar{x}^{2}}$

$\hat{a}=\bar{y}-\hat{b}\bar{x}.$

$\hat{y}=\hat{b}x+\hat{a}$

图例：

2.3 判定指标

（1）决定系数

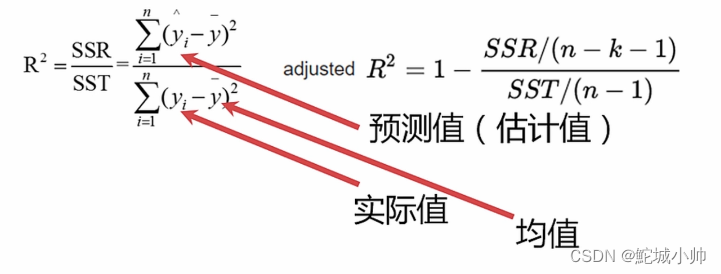
R方（决定系数）：R方是衡量回归模型拟合优度的指标，表示因变量的方差能够被自变量解释的比例。R方的取值范围在0到1之间，值越接近1表示模型的拟合效果越好。

调整R方：由于R方倾向于增加自变量的数量而提高，为了避免过拟合问题，可以使用调整R方，考虑模型中自变量的数量和样本量，更准确地评估模型的拟合效果。

（2）残差不相关（DW检验）

残差分析：通过分析回归模型的残差（预测值与实际值之间的差异）来评估模型的拟合效果。可以检查残差是否满足模型的假设，如正态性、独立性和同方差性等。

3. 主成分分析

3.1 概述

主成分分析（Principal Component Analysis，PCA）是一种常用的降维技术和数据预处理方法，用于将高维数据转换为低维数据，并发现数据中的主要变化方向。

3.2 分析步骤

主成分分析的步骤如下：

数据标准化：对原始数据进行标准化处理，使得每个变量具有相同的尺度，以避免某些变量对主成分分析结果的影响过大。
协方差矩阵计算：计算标准化后的数据的协方差矩阵，反映了各个变量之间的线性相关性。
特征值和特征向量计算：对协方差矩阵进行特征值分解，得到特征值和对应的特征向量。特征值表示了主成分的重要性，特征向量表示了主成分的方向。
主成分选择：根据特征值的大小选择保留的主成分数量。一般来说，可以根据特征值的累计贡献率来确定保留的主成分数量，通常选择累计贡献率达到一定阈值（如80%或90%）的主成分。
主成分计算：根据选择的主成分数量，将标准化后的数据投影到选定的主成分上，得到降维后的数据。

3.3 示例

A	B	C	D
10	7	9	2
10	19	8	5
10	15	10	7
10	6	7	10

表里的每个属性都是一个维度，每一行数据是四个维度，构成一个向量。

4. 编码-正态分布

4.1 偏峰度-检测是否为正态分布

import numpy as np
import scipy.stats as ss

# 生成符合正态分布的20个数
norm_dist=ss.norm.rvs(size=20)
norm_dist
Out[8]: 
array([-0.35253314,  1.30905351, -0.87697959, -0.81013325,  0.43607702,
       -0.86658611,  0.39143501, -0.49922316, -0.64487584,  1.20674725,
       -0.22658859, -0.20677417, -0.50409745,  1.35071198,  0.15582528,
        0.55242563, -0.15331266,  0.53300935,  0.55837149, -0.91415605])

# 分析是否符合正态分布
ss.normaltest(norm_dist)
Out[9]: NormaltestResult(statistic=2.001448058781207, pvalue=0.36761318204518334)

上述分析结果，统计值为2.00，P值为0.367。它是符合当前假设，即符合正态分布的。这里的normaltest() 是基于偏度和峰度的检验法

4.2 卡方检验 - 是否为正态分布

	男	女
化妆	15（55）	95（55）	110
不化妆	85（45）	5（45）	90
	100	100	200

计算公式： $x^{^{2}}=\sum_{i=1}^{k}\frac{(f_{i}-np_{i})^2}{np_{i}}$

对照表：

P	0.99	0.95	0.90	0.70	0.50	0.30	0.10	0.05	0.01
卡方	0.00016	0.004	0.016	0.148	0.455	1.074	2.706	3.841	6.635

使用python代码检验：

ss.chi2_contingency([[15,95],[85,5]])
Out[10]: 
Chi2ContingencyResult(statistic=126.08080808080808, pvalue=2.952141400507898e-29, dof=1, expected_freq=array([[55., 55.],
       [45., 45.]]))

根据python校验结果，得出卡方值为126.0，P值为2.952141400507898e-29（无限小），自由度为1，array 是理论分布。

4.3 独立分布 t 检验（例）

公式： $t=\frac{\bar{X_{1}}-\bar{X_{2}}}{\sqrt{\frac{(_{n_{1}-1})S_{1}^{2}+(_{n_{2}-1})S_{2}^{2}}{n_{1}+n_{2}-2}}(1/n_{1}+1/n_{2})}$

代码实现：

# ss.norm.rvs是标准正态分布生成10个数，ss.norm.rvs是标准正态分布生成20个数
ss.ttest_ind(ss.norm.rvs(size=10),ss.norm.rvs(size=20))
Out[11]: Ttest_indResult(statistic=-0.5705942877670696, pvalue=0.5728257925000966)

上述结果：得出检验统计量为-0.570，P值为0.572> 0.05，可以接受假设是成立的，即两次生成数的均值是没有差别的。

需知，当数量小的情况下，P值大于0.05，那么，当两组数的量更大后，比如：100个和200个数，它们的均值会更加符合假设，也就是说，比较值的量越大越稳定。

4.4 方差校验

数据分为m组，共n个采样：3组，共15个采样

编号	电池寿命
编号	甲	乙	丙
1	49	28	38
2	50	32	40
3	39	30	45
4	40	26	42
5	43	34	48

在前面用公式得出的结果是：

SSM = 604.93

SSE = 206

F = 17.6 # 检验统计量

P = 0.00027 < 0.05 # P值

使用python代码检验：

# 方差校验三组数据
ss.f_oneway([49,50,39,40,43],[28, 32, 30, 26, 34], [38, 40, 45, 42, 48])
Out[12]: F_onewayResult(statistic=17.619417475728156, pvalue=0.0002687153079821642)

由结果可知，检验结果与前面的计算结果基本一致。P值约等于 0.00027 < 0.05 。接受假设，这几组的均值没有差异。

4.5 QQ图

4.5.1概述

QQ图（Quantile-Quantile plot）是一种用于检验数据是否符合某种理论分布的方法。它通过将数据的分位数与理论分布的分位数进行比较，来评估数据与理论分布之间的偏差程度。

下面是使用QQ图进行检验的一般步骤：

收集样本数据。
根据所假设的理论分布（例如正态分布），计算样本数据的理论分位数。
对样本数据进行排序，计算其实际的分位数。
绘制QQ图，将实际分位数作为横轴，理论分位数作为纵轴。
观察QQ图中数据点的分布情况。如果数据点基本上沿着一条直线分布，与理论分布的分位数对应良好，那么可以认为数据符合所假设的理论分布。如果数据点明显偏离直线，那么可以怀疑数据与理论分布存在偏差。
可以使用一些统计量来量化数据与理论分布之间的偏差程度，例如斜率、拟合度等。这些统计量可以帮助进一步判断数据的符合度。

需要注意的是，QQ图并不能确定数据是否绝对符合某个理论分布，它只是一种可视化工具，用于检查数据与理论分布之间的整体趋势和偏差程度。因此，对于具体的判断和结论，还需要综合考虑其他统计方法和领域知识。

4.5.2 python函数分析

import matplotlib
matplotlib.use('TkAgg')

import scipy.stats as ss
from statsmodels.graphics.api import qqplot
import matplotlib.pyplot as plt

# 生成100个标准正态分布式，并使用QQ图校验
fig = qqplot(ss.norm.rvs(size=100))
# 根据检验结果创建QQ图
plt.show()

QQ图：

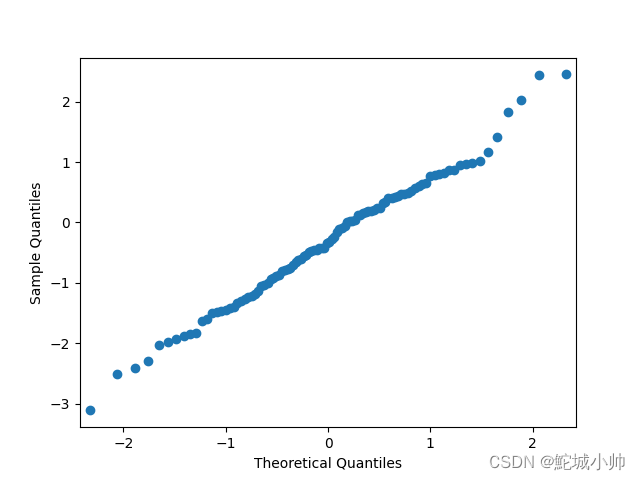
在分析 QQ 图时，我们通常会关注曲线是否接近一条直线，该直线代表理论分布（例如正态分布）。如上图， QQ 图的曲线基本分布在角平分线上，而个别点在顶部或底部偏离，这通常是正常的，尤其在样本量较小的情况下。

因此，如果大多数点接近角平分线，而只有少数个别点偏离，我们可以初步认为数据基本符合正态分布。

4.6 相关系数

4.6.1 Pearson相关系数

import pandas as pd
s1=pd.Series([0.1, 0.2, 1.1, 2.4, 1.3, 0.3, 0.5])
s2=pd.Series([0.5, 0.4, 1.2, 2.5, 1.1, 0.7, 0.1])
s1.corr(s2)
Out[6]: 0.9333729600465923

通过计算s1和s2的相关系数，得到的结果是0.9333729600465923。这个结果表示s1和s2之间存在一个强正相关关系，接近于1，说明两个变量具有高度的线性相关性。

4.6.2 Spearman相关系数

（1）示例一：

# 斯皮尔曼相关系数
s1.corr(s2,method="spearman")
Out[7]: 0.7142857142857144

通过s1.corr(s2, method="spearman")计算得到的结果0.7142857142857144是斯皮尔曼相关系数。斯皮尔曼相关系数是一种非参数的排名相关系数，用于衡量两个变量之间的单调关系，而不是线性关系。该系数的取值范围为-1到1，其中1表示完全的正相关，-1表示完全的负相关，0表示没有单调关系。

在这个例子中，斯皮尔曼相关系数为0.7142857142857144，表明两个变量之间存在着一定的正相关关系，但并非完全的线性关系。

（2）示例二：

import numpy as np

df=pd.DataFrame([s1,s2])
df.corr()
Out[9]: 
     0    1    2    3    4    5    6
0  1.0  1.0  1.0  1.0 -1.0  1.0 -1.0
1  1.0  1.0  1.0  1.0 -1.0  1.0 -1.0
2  1.0  1.0  1.0  1.0 -1.0  1.0 -1.0
3  1.0  1.0  1.0  1.0 -1.0  1.0 -1.0
4 -1.0 -1.0 -1.0 -1.0  1.0 -1.0  1.0
5  1.0  1.0  1.0  1.0 -1.0  1.0 -1.0
6 -1.0 -1.0 -1.0 -1.0  1.0 -1.0  1.0

# 创建一个二维数组，每一列代表一个Series对象的值
array = np.array([s1, s2]).T

# 使用二维数组创建DataFrame对象
df = pd.DataFrame(array)

# 计算DataFrame对象的相关系数矩阵
df.corr()
Out[13]: 
          0         1
0  1.000000  0.933373
1  0.933373  1.000000

#  获取斯皮尔曼矩阵
df.corr(method="spearman")
Out[14]: 
          0         1
0  1.000000  0.714286
1  0.714286  1.000000

在上述代码示例中，通过df.corr()计算得到了两个DataFrame之间的相关系数矩阵。请注意，DataFrame的默认相关系数计算是基于皮尔逊相关系数的，这适用于连续变量之间的线性关系。

在第一个相关系数矩阵中，每个元素表示两个变量之间的皮尔逊相关系数。由于s1和s2的值都是一样的，因此相关系数矩阵的对角线上的值都为1，表示每个变量与自身的完全正相关。

在第二个相关系数矩阵中，使用np.array([s1,s2]).T创建了一个新的DataFrame，使得s1和s2成为该DataFrame的两列。然后通过df.corr()计算得到的相关系数矩阵，此时得到的是两个变量之间的皮尔逊相关系数。在这个矩阵中，每个元素表示两个变量之间的线性关系程度，其中第(0, 1)和(1, 0)位置的值为0.933373，表示s1和s2之间存在较强的线性相关性。

最后，在第三个相关系数矩阵中，通过df.corr(method="spearman")计算得到的是斯皮尔曼相关系数矩阵。斯皮尔曼相关系数是一种非参数的排名相关系数，用于衡量两个变量之间的单调关系。在这个矩阵中，每个元素表示两个变量之间的单调关系程度。在(0, 1)和(1, 0)位置的值为0.714286，表示s1和s2之间存在一定的单调关系。

因此，df.corr(method="spearman")计算得到的相关系数矩阵是基于斯皮尔曼相关系数的，表示各列之间的单调关系程度。在你的示例中，该矩阵显示了每对变量之间的斯皮尔曼相关系数。

综上所述，相关系数矩阵可以用来衡量变量之间的线性关系（皮尔逊相关系数）或单调关系（斯皮尔曼相关系数）。具体选择哪种相关系数取决于变量类型和分析目的。

4.7 回归

import numpy as np

# 创建一个包含10个元素的一维数组，并将其转换为二维数组，形状为(10, 1)
x = np.arange(10, dtype=float).reshape((10, 1))

# 生成一个包含10个随机数的一维数组，并将其转换为二维数组，形状为(10, 1)
random_array = np.random.random((10, 1))

# 计算 y 值，根据公式 y = x * 3 + 4 + 随机数
y = x * 3 + 4 + random_array

x
Out[25]: 
array([[0.],
       [1.],
       [2.],
       [3.],
       [4.],
       [5.],
       [6.],
       [7.],
       [8.],
       [9.]])
y
Out[26]: 
array([[ 4.55591316],
       [ 7.50013161],
       [10.00540416],
       [13.0842534 ],
       [16.60159057],
       [19.93834815],
       [22.59267395],
       [25.36910513],
       [28.39982194],
       [31.75504123]])

上述代码，创建了一个形状为 (10, 1) 的浮点数数组 x，并使用随机数创建了另一个形状相同的数组 y。y 的值是根据 x 的值计算得出的，每个元素乘以 3，加上 4，并加上一个来自均匀分布的随机数。

from sklearn.linear_model import LinearRegression

# 创建线性回归模型对象
reg = LinearRegression()

# 使用线性回归模型拟合数据
res = reg.fit(x, y)

# 使用拟合的模型对输入数据进行预测
y_pred = reg.predict(x)

# 打印预测结果
y_pred
# Output:
# array([[ 4.35012354],
#        [ 7.37903572],
#        [10.40794789],
#        [13.43686007],
#        [16.46577224],
#        [19.49468442],
#        [22.52359659],
#        [25.55250877],
#        [28.58142094],
#        [31.61033312]])

# 打印回归系数（斜率）
reg.coef_
# Output: array([[3.02891218]])

# 打印截距
reg.intercept_
# Output: array([4.35012354])

4.8 主成分分析

4.8.1 示例一

# 创建一个二维数组
data=np.array([np.array([2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]), np.array([2.4, 0.7, 2.9, 2.2, 3, 2.7, 1.6, 1.1, 1.6, 0.9])]).T
data
Out[40]: 
array([[2.5, 2.4],
       [0.5, 0.7],
       [2.2, 2.9],
       [1.9, 2.2],
       [3.1, 3. ],
       [2.3, 2.7],
       [2. , 1.6],
       [1. , 1.1],
       [1.5, 1.6],
       [1.1, 0.9]])
from sklearn.decomposition import PCA

# 创建PCA对象并指定降维后的维度为1
lower_dim=PCA(n_components=1)

# 在原始数据上进行PCA降维
lower_dim.fit(data)
Out[43]: PCA(n_components=1)

# 输出降维后的数据所解释的方差比例
lower_dim.explained_variance_ratio_
Out[44]: array([0.96318131]) # 输出: [0.96318131]

lower_dim.fit_transform(data)
Out[45]: 
array([[-0.82797019],
       [ 1.77758033],
       [-0.99219749],
       [-0.27421042],
       [-1.67580142],
       [-0.9129491 ],
       [ 0.09910944],
       [ 1.14457216],
       [ 0.43804614],
       [ 1.22382056]])

以上代码利用sklearn.decomposition模块中的PCA类进行主成分分析。通过创建PCA对象并指定降维后的维度为1，然后调用fit()方法在原始数据上进行PCA降维。降维后的数据可通过调用fit_transform()方法获得，输出的结果是一个二维数组，每行表示一个样本在降维后的空间中的坐标。

主成分分析的结果可以通过explained_variance_ratio_属性获取，它表示每个主成分所解释的方差比例。在这个例子中，降维后的第一个主成分可以解释约96.3%的方差。

4.8.2 示例二

import pandas as pd
import numpy as np
def myPCA(data, n_components=100000000):
    # 计算均值向量
    mean_vals=np.mean(data, axis=0)  
    # 数据中心化
    mid=data-mean_vals
    # 计算协方差矩阵
    cov_mat=np.cov(mid,rowvar=False)
    # 利用线性代数库计算特征值和特征向量
    from scipy import linalg
    eig_vals,eig_vects=linalg.eig(np.mat(cov_mat))
    # 对特征值进行排序，取前n_components个特征向量
    eig_val_index=np.argsort(eig_vals)
    eig_val_index=eig_val_index[:-(n_components+1):-1]
    eig_vects=eig_vects[:,eig_val_index]
    # 计算降维后的数据
    low_dim_mat=np.dot(mid,eig_vects)
    return low_dim_mat,eig_vals
data=np.array([np.array([2.5, 0.5, 2.2, 1.9, 3.1, 2.3, 2, 1, 1.5, 1.1]), np.array([2.4, 0.7, 2.9, 2.2, 3, 2.7, 1.6, 1.1, 1.6, 0.9])]).T
# 调用自定义的PCA函数进行降维
print(myPCA(data,n_components=1))

以上代码定义了一个自定义的PCA函数myPCA，用于进行主成分分析。该函数接受一个数据矩阵和可选的降维维度参数。函数首先计算数据的均值向量，然后将数据中心化，接着计算协方差矩阵。利用线性代数库中的特征值分解函数，计算出特征值和特征向量。对特征值进行排序，取前n_components个特征向量，然后利用这些特征向量对数据进行降维。最后函数返回降维后的数据和特征值。

在代码的最后，调用myPCA函数对给定的数据进行降维，将降维后的数据和特征值打印输出。