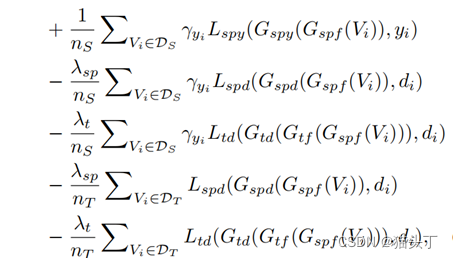摘要

本实验通过建立基于耦合 Lorenz 63 模式的孪生实验框架，使用集合调整卡尔曼滤波器EAKF实现参数估计，测试参数估计开始的不同阶段、观测误差、同化频率、协方差膨胀等方法细节对于参数估计结果的影响。

耦合 Lorenz 63 模式

Lorenz 63 模式是Lorenz于1963年从Saltzman提供的控制方程中推导简化出的新的动力模型，被广泛用来验证各类同化算法。Lorenz 63 模式耦合上平板的海洋模式构成概念海气耦合模式，耦合 Lorenz 63 模式的动力学模型可以写成
$\frac{dx_1}{dt}= -\sigma x_1 + \sigma x_2$
$\frac{dx_2}{dt}= -x_1 x_3 + (1 + c_1 w) \kappa x_1 - x_2$
$\frac{dx_3}{dt}= x_1 x_2 - b x_3$
$O_m \frac{dw}{dt} = c_2 x_2 - O_d w + S_m + S_s cos(2 \pi t / S_{pd} )$
其中， $x_1$ 、 $x_2$ 、 $x_3$ 为大气模式的高频率状态变量，大气模式的参数 $\sigma$ 、 $\kappa$ 、 $b$ 的标准值为9.95、28、8/3。状态变量 $w$ 作为缓慢变化的海洋引入，快速的大气模式与缓慢的海洋模式通过耦合系数 $c_1$ 、 $c_2$ 耦合。耦合模式的标准参数值 $(\sigma, \kappa, b, c_1, c_2, O_m, O_d, S_m, S_s, S_pd) = (9.95, 28, 8/3, 0.1, 1, 10, 1, 10, 1, 10)$ 。

In:

# 定义模式 
import numpy as np

# Lorenz 63 模式的右端项
def L63_rhs(x, Para, t):
    # x是初值，Para是参数
    # 右端项有forcing，因此是关于时刻t的
    dx = np.ones_like(x);
#    {sigma,kappa,beta,c1,c2,Om,Od,Sm,Ss,Spd}   # 参数
#    {9.95, 28, 8/3, 0.1, 1, 1, 10, 10, 1, 10}   # 标准参数
    sigma = Para[0]; kappa = Para[1]; beta = Para[2];  # "atmospheric" para.
    c1 = Para[3]; c2 = Para[4]     # couple para
    Om = Para[5]; Od = Para[6]     # scale para
    Sm = Para[7]; Ss = Para[8]; Spd = Para[9]   # external forcing para
    
    St = Sm + Ss * np.cos(2 * np.pi * t / Spd)
    
    dx[0] = sigma * (x[1] - x[0])
    dx[1] = (1 + c1 * x[3]) * kappa * x[0] - x[1] - x[0] * x[2]
    dx[2] = x[0] * x[1] - beta * x[2]
    dx[3] = (c2 * x[1] - Od * x[3] + St) / Om
    return dx

# Runge-Kutta 4-5 算法用于求解ODE
def RK45(x, func, h):
    K1 = func(x);
    K2 = func(x + h / 2 * K1);
    K3 = func(x + h / 2 * K2);
    K4 = func(x + h * K3);
    x1 = x + h / 6 * (K1 + 2 * K2 + 2 * K3 + K4)
    return x1

# L63模式利用RK-45算法积分一步，即模式积分
# x0是初值，delta_t是步长，Para是参数
def L63_adv_1step(x0, delta_t, Para, t):
    x1 = RK45(x0, lambda x:L63_rhs(x, Para, t), delta_t)
    return x1

EAKF 同化方法

EAKF算法是一种一种针对非线性非高斯系统的卡尔曼滤波算法，EAKF全称为Ensemble Adjustment Kalman Filter。与传统的卡尔曼滤波不同，EAKF算法使用集合统计学的方法，通过多次运行卡尔曼滤波器并对结果进行集成来估计系统的状态。

EAKF算法的主要思想是通过在卡尔曼滤波器中引入噪声来代替传统卡尔曼滤波的线性扰动模型，同时利用集合统计学的方法来估计状态的分布。具体来说，EAKF算法将初始状态的估计值分为多个成员（ensemble）并通过多次运行滤波器，每次都使用不同的初始值，来得到多个状态估计值。然后，这些成员的状态值可以被用来计算状态的统计分布，并作为预测值的不确定性度量。

EAKF算法的优点是可以更好地处理非线性、非高斯的系统，同时也具有很好的并行性。但是，由于在每个时间步中需要运行多个卡尔曼滤波器，因此具有较高的计算成本。

在针对每个标量观测的同化中，顺序EAKF算法对观测变量和模型状态变量的先验分布之间的关系作出（局部）最小二乘假设。在这种情况下，分析过程可以分为两部分进行：首先，通过应用针对标量的集合滤波器，为观测变量的每个先验集合计算更新增量。第二，执行每个状态变量对观测变量先验集合样本的线性回归，以根据相应的观测增量计算每个状态变量集合成员的更新增量。具体算法如下：

第一步，顺序EAKF算法首先将标量观测算子 $h$ 应用于状态的每个集合样本，从而产生观测投影的先验集合

$\begin{equation} y_{p, n}=h\left(x_{p, n}\right), n=1, \ldots, N \end{equation}$

然后利用集合样本计算观测投影的先验估计的样本均值 $\bar{y}_p$ 和样本方差 $\sigma_p^2$ 。给定（标量）观测值 $y^o$ 和观测误差方差 $\sigma_o^2$ ，先验值和似然值的乘积产生一个更新的估计，其方差为
$\begin{equation} \sigma_u^2=\left[\left(\sigma_p^2\right)^{-1}+\left(\sigma_o^2\right)^{-1}\right]^{-1} \end{equation}$
均值为
$\begin{equation} \bar{y}_u=\sigma_u^2\left(\bar{y}_p / \sigma_p^2+y^0 / \sigma_o^2\right) \end{equation}$
那么在观测空间里面的 $y$ 的后验集合为
$\begin{equation} y_{u, n}=\left(\sigma_u / \sigma_p\right)\left(y_{p, n}-\bar{y}_p\right)+\bar{y}_u \end{equation}$
其中的每个集合成员 $y_{u,n}$ 是通过移动平均值并对先验集合成员进行线性收缩来构成的。平移和收缩的操作使的样本均值为 $\bar{y}_p$ ，方差精确为 $\sigma_u^2$ 。观测空间的增量集合定义为 $\Delta y_n=y_{u, n}-y_{p, n}$ 。

第二步，顺序EAKF通过使用先验的联合集合样本统计关系将观测空间增量回归到状态向量分量上，独立计算每个状态向量分量的增量如下

$\begin{equation} \Delta x_{m, n}=\left(\sigma_{x m, y} / \sigma_p^2\right) \Delta y_n \end{equation}$

在上式中， $\Delta x_{m, n}$ 是状态向量分量 $m$ 的集合成员 $n$ 的增量，而 $\sigma_{xm},y$ 是状态向量分量 $m$ 和 $y$ 的先验样本协方差。（43）中的项 $\sigma_{x m, y} / \sigma_p^2$ 是卡尔曼增益在顺序EAKF中的形式。

In:

# 定义EAKF同化方法：
# (L63模式无需局地化)
def comp_cov_factor(z_in, c):
    z = abs(z_in)
    if z <= c:
        r = z/c;
        cov_factor = (((-0.25 * r + 0.5) * r + 0.625) * r - 5.0 / 3.0) * r**2 + 1.0
    elif z >= c * 2.0:
        cov_factor=0.0;
    else:
        r = z / c;
        cov_factor = ((((r / 12.0 - 0.5) * r + 0.625) * r + 5.0 / 3.0) * r - 5.0) * r + 4.0 - 2.0 / (3.0 * r)
    return cov_factor
# 观测增量
def obs_increment_eakf(ensemble, observation, obs_error_var):
    prior_mean = np.mean(ensemble)
    prior_var = np.var(ensemble)
    if prior_var > 0.1:
        post_var = 1.0 / (1.0 / prior_var + 1.0 / obs_error_var)
        post_mean = post_var * (prior_mean / prior_var + observation / obs_error_var)
    else:
        post_var = prior_var
        post_mean = prior_mean
    
    updated_ensemble = ensemble - prior_mean + post_mean

    var_ratio = post_var / prior_var;
    updated_ensemble = np.sqrt(var_ratio) * (updated_ensemble - post_mean) + post_mean

    obs_increments = updated_ensemble - ensemble
    return obs_increments
# 模式增量
def get_state_increments(state_ens, obs_ens, obs_incs):
    covar = np.cov(state_ens, obs_ens)
    state_incs = obs_incs * covar[0,1] / covar[1, 1]
    return state_incs
# 分析过程

def eakf_analysis(ensemble_in, obs_in, obs_error_var_vec):
    # obs_error_var_vec 是一个矢量，对应obs_in的每个entry的方差
    L = len(ensemble_in[0]);     # model dimension (model grids)
    m = len(obs_in);    # number of obs sites
    for i in range(m):
        ensemble_proj = ensemble_in; 
        obs_proj = ensemble_proj[:, i];   # project model grid to obs site
        obs_error_var = obs_error_var_vec[i]
        obs_inc = obs_increment_eakf(obs_proj, obs_in[i], obs_error_var)
        for j in range(L):
            # no localization for L63
            state_inc = get_state_increments(ensemble_in[:, j], obs_proj, obs_inc)
            ensemble_in[:, j] = ensemble_in[:, j] + state_inc
    ensemble_out = ensemble_in;
    return ensemble_out

def eakf_analysis_pe(ensemble_in,obs_in,ensemble_proj,obs_error_var_vec):
     # 差别在于观测投影是关于模式集合的观测，而非参数的观测，参数的观测投影是implicit
     # ensemble_in 是参数集合
    if len(ensemble_in.shape) > 1:
        L = len(ensemble_in[0])     
    else:
        L = 1
    m = len(obs_in);    # number of obs sites
    for i in range(m):
        obs_proj = ensemble_proj[:,i];   # project model grid to obs site
        obs_error_var = obs_error_var_vec[i]
        obs_inc = obs_increment_eakf(obs_proj, obs_in[i], obs_error_var)
        if L > 1:
            for j in range(L):
                # no localization for L63
                state_inc = get_state_increments(ensemble_in[:, j], obs_proj, obs_inc)
                ensemble_in[:, j] = ensemble_in[:, j] + state_inc
        else:
            state_inc = get_state_increments(ensemble_in, obs_proj, obs_inc)
            ensemble_in = ensemble_in + state_inc
    ensemble_out = ensemble_in
    return ensemble_out

孪生实验

在现实情况下，真实的状态值是未知的，而且有噪声的测量值是由传感设备收集的。然而，为了测试算法，需要事先知道真实的状态，以便评估所开发算法的收敛性和准确性。在这个意义上，孪生实验的概念在数据同化（和一般的反问题）研究中很受欢迎。首先，根据其动力模型和实际情况的相似性，选择一个原型测试案例（也被叫做“玩具问题”）。类似于你的第一个 "Hello World!"程序。Lorenz 63 和Lorenz 96 经常用于数值天气预报研究。通过固定所有参数和运行正向积分求解器，计算出一个参考的真实轨迹，直到达到某个最终时间。然后通过在空间和时间的某些点上对真实轨迹进行取样来收集合成观测值。可以对真实状态变量进行映射，并人为地添加任意的随机噪声（例如，高斯白噪声）。最后，使用感兴趣的数据同化技术，从错误的状态变量初值或不准确的模型参数利用合成的观测数据开始同化实验。因此，算法的输出轨迹与参考方案进行比较，可以评估其性能。孪生实验可以廉价地评估不同的测量稀疏度和/或噪声水平的影响，而不需要定位或修改传感器。

In:

#%% 孪生实验
# 1. spin-up获取真实场初值
import os
ParaTrue = np.array([9.95, 28.0, 8/3, 0.1, 1, 10, 1, 10, 1, 10])  # k=28, Om = 10, Od = 1
delta_t = 0.01

if os.path.exists('L63ext_x0true.npz'):    
    # 读取初值
    with np.load('L63ext_x0true.npz') as INIT_STATE:
        x0true = INIT_STATE['x0true']
        delta_t = INIT_STATE['delta_t']
        ParaTrue = INIT_STATE['ParaTrue']
        print('x0true and ParaTrue loaded')
        print('initial conditions [x1, x2, x3, w] = ' + str(x0true))
else:
    # spin-up 1000000步
    # 确定初始条件 (x1, x2, x3, w)
    x0 = np.array([0,1,0,0])
    t = 0
    while t < 1000000:
        x1 = L63_adv_1step(x0, delta_t, ParaTrue, t*delta_t)
        t += 1
        x0 = x1    
    x0true = x0
    np.savez('L63ext_x0true.npz', x0true = x0, delta_t = delta_t, ParaTrue = ParaTrue)
    print('spin-up finished')

  
# 2. 造真值
assim_period_steps = 10000

if os.path.exists('L63ext_Xtrue.npz'):
    # 读取Truth
    with np.load('L63ext_Xtrue.npz') as TRUE_STATE:
        Xtrue = TRUE_STATE['Xtrue']
        assim_period_steps = TRUE_STATE['steps']
        print('True States loaded')
else:
    Xtrue = np.zeros([assim_period_steps,4])
    Xtrue[0] = x0true
    for t in range(assim_period_steps - 1):
        Xtrue[t + 1] = L63_adv_1step(Xtrue[t], delta_t, ParaTrue, t*delta_t)
    np.savez('L63ext_Xtrue', Xtrue = Xtrue, steps = assim_period_steps)
    print('True States generated')
        
nsteps = assim_period_steps

# 3. 造观测
# 每多少步观测一次
nt = 10;  # 同化频率，尝试 2、5、10、20、50、100
obs_error_atm = 2  # 大气观测标准差，尝试0.5、1、2、5
obs_error_ocn = 0.5  # 海洋观测标准差，尝试0.5、1、2、5

OBS = np.zeros([nsteps//nt, 4]);
for t in range(nsteps//nt):
    OBS[t, 0:3] = Xtrue[nt*t, 0:3] + obs_error_atm * np.random.randn(3)
    OBS[t, 3] = Xtrue[nt*t, 3] + obs_error_ocn * np.random.randn(1)
print('OBS data generated')

Out:

x0true and ParaTrue loaded
initial conditions [x1, x2, x3, w] = [-12.03416588 -19.93560174  45.25578754   9.60091586]
True States loaded
OBS data generated

同化实验

采用控制变量法，测试参数估计开始的不同阶段、观测误差、同化频率等方法细节对于参数估计结果的影响。实验设置如下表。

参数估计开始阶段	同化频率	大气观测标准差	海洋观测标准差
0	10	0.5	0.5
1000	20	1	1
2000	50	2	2
4000	100	5	5

In:

#%% 同化实验
assim_steps = 5000 # 同化步数
N = 50          # 集合成员数
n_startPE = 1000  # 何时开始参数估计，尝试 0, 1000, 2000, 4000
para_idx = 1    # 待估计参数的索引
infl = 1.05     # 状态膨胀 inflation
pinfl = 1.04;   # 参数膨胀 inflation

import numpy as np
Xassim = np.zeros_like(Xtrue)      # 包含了同化的和未同化的
Xspread = np.zeros_like(Xtrue)
Para = ParaTrue    
Para[para_idx] = 30   # 假设仅仅第二个参数 k 有偏
Passim = np.zeros(len(OBS))         # 只考虑一个参数，只在同化时更新 
obs_var = np.zeros(4)
obs_var[0:3] = obs_error_atm
obs_var[3] = obs_error_ocn

import os
# 状态集合的产生或者读取
InitEnsPath = './L63InitialEns' + str(N) + '.npz'

if os.path.exists(InitEnsPath):       # 如果已经有初始集合，就读取，否则造一个
    with np.load(InitEnsPath) as ExprInitEns:
        Ens0 = ExprInitEns['arr_0'];
        print('Initial Ensemble loaded: N = ' + str(N))
else:
    Ens0 = np.zeros((N, 4))
    for n in range(N):
        Ens0[n] = OBS[0] + 2 * np.random.randn(4)      # 基于初始的猜测造观测        
    print('Initial Ensemble generated: N = ' + str(N))
    np.savez(InitEnsPath, Ens0)

# 参数集合的产生或者读取
InitParaPath = './L63ParaEns' + str(N) + '.npz'

if os.path.exists(InitParaPath):       # 如果已经有初始参数集合，就读取，否则造一个
    with np.load(InitParaPath) as ExprPARAEns:  
        PARAS = ExprPARAEns['undefP']
        print('Initial Parameter Ensemble loaded: N = ' + str(N))
else:
    PARAS = np.zeros(N)
    for n in range(N):
        PARAS[n] = Para[para_idx] + 2 * np.random.randn(1) 
    print('Initial Parameter Ensemble generated: N = ' + str(N))
    np.savez(InitParaPath, undefP = PARAS)

Xassim[0] = np.mean(Ens0, axis=0)  # 初始状态集合平均值
Passim[range(n_startPE//nt + 1)] = Para[para_idx]     # 如果不参数估计，就全部使用非集合的参数

#  同化循环
Ens = Ens0
Ens2 = np.zeros_like(Ens)
for t in range(assim_steps):
    for n in range(N):      # 积分模式
        if t > n_startPE:
            Para_i = Para; Para_i[para_idx] = PARAS[n]
            Ens2[n] = L63_adv_1step(Ens[n], delta_t, Para_i, t*delta_t)
        else:
            Ens2[n] = L63_adv_1step(Ens[n], delta_t, Para, t*delta_t)
        
    if t%nt == 0:    # 判定同化       
        # 状态inflation
        Ens_mean = np.mean(Ens2, axis=0);
        for n in range(N):      # inflation (prior_inf)
            Ens2[n] = (Ens2[n] - Ens_mean) * infl + Ens_mean   
        # 状态估计
        Ens2 = eakf_analysis(Ens2, OBS[t//nt], obs_var)  
        
        if t > n_startPE:     # 判定参数估计        
             # 参数inflation
            PARAm = np.mean(PARAS)
            for n in range(N):
                PARAS[n] = PARAm + pinfl * (PARAS[n] - PARAm)
            # 参数估计    
            PARAS2 = eakf_analysis_pe(PARAS, OBS[t//nt], Ens2, obs_var)
            PARAS = PARAS2
            Passim[t//nt] = np.mean(PARAS2)              
    else:
        pass
    Xassim[t] = np.mean(Ens2, axis=0)
    Xspread[t] = np.std(Ens2, axis=0)
    Ens = Ens2

Out:

Initial Ensemble loaded: N = 50
Initial Parameter Ensemble loaded: N = 50

绘图

In:

#%% 绘图
import matplotlib.pyplot as plt
plt.figure(figsize = (18, 18))
x_plt_range = np.array((range(4000, 5000)))
x_obs_range = np.array(range(4000 + nt, 5000 + nt, nt))
x_obs_idx_r = np.array(range(4000//nt, 5000//nt))

w_plt_range = np.array(range(5000))
w_obs_range = np.array(range(nt, 5000 + nt, nt))
w_obs_idx_r = np.array(range(5000//nt))

plt.subplot(3, 1, 1)
# 报错则
# [i * delta_t for i in x_plt_range] 替换 x_plt_range * delta_t
plt.plot(x_plt_range * delta_t, Xtrue[x_plt_range, 1], 'k-', lw = 3, label = 'True')
plt.plot(x_obs_range * delta_t, OBS[x_obs_idx_r, 1], 'r*', lw = 3, ms = 8, mew = 1, label = 'OBS')
plt.plot(x_plt_range * delta_t, Xassim[x_plt_range, 1], 'b', lw = 3, label = 'EAKF_mean')
plt.ylabel('$x_2$', fontsize = 16)
plt.yticks(range(-40, 60, 20), fontsize = 16)
plt.xlim(40, 50)
plt.xticks(range(40, 52, 2), fontsize = 16)
plt.legend(fontsize = 18, ncol = 3)
plt.grid()
    
plt.subplot(3, 1, 2)    
plt.plot(w_plt_range * delta_t, Xtrue[w_plt_range, 3], 'k-', lw = 3, label = 'True')
plt.plot(w_obs_range * delta_t, OBS[w_obs_idx_r, 3], 'r*', lw = 3, ms = 8, mew = 1, label = 'OBS')
plt.plot(w_plt_range * delta_t, Xassim[w_plt_range, 3], 'b', lw =3, label = 'EAKF_mean')
plt.ylabel('w', fontsize = 16)
plt.yticks(range(5, 14, 2), fontsize = 16)
plt.xlim(0, 50)
plt.xticks(range(0, 60, 10), fontsize = 16)
plt.legend(fontsize = 18, ncol = 3)
plt.grid()
    
    
plt.subplot(3, 1, 3)
plt.plot(w_obs_range * delta_t, Passim[w_obs_idx_r], 'r',lw = 3, ms = 8, mew = 1, label = 'PE estimation')
plt.plot(w_obs_range * delta_t, 28*np.ones(w_obs_idx_r[-1] + 1), 'k:', lw = 3, label = 'True Para.')
plt.ylabel('$\kappa$', fontsize = 16)
plt.xlabel('Time Units', fontsize = 16) 
plt.yticks(range(26, 32, 1), fontsize = 16)
plt.xlim(0, 50)
plt.xticks(range(0, 60, 10), fontsize = 16)
plt.legend(fontsize = 18, ncol = 2)
plt.grid()

Out:

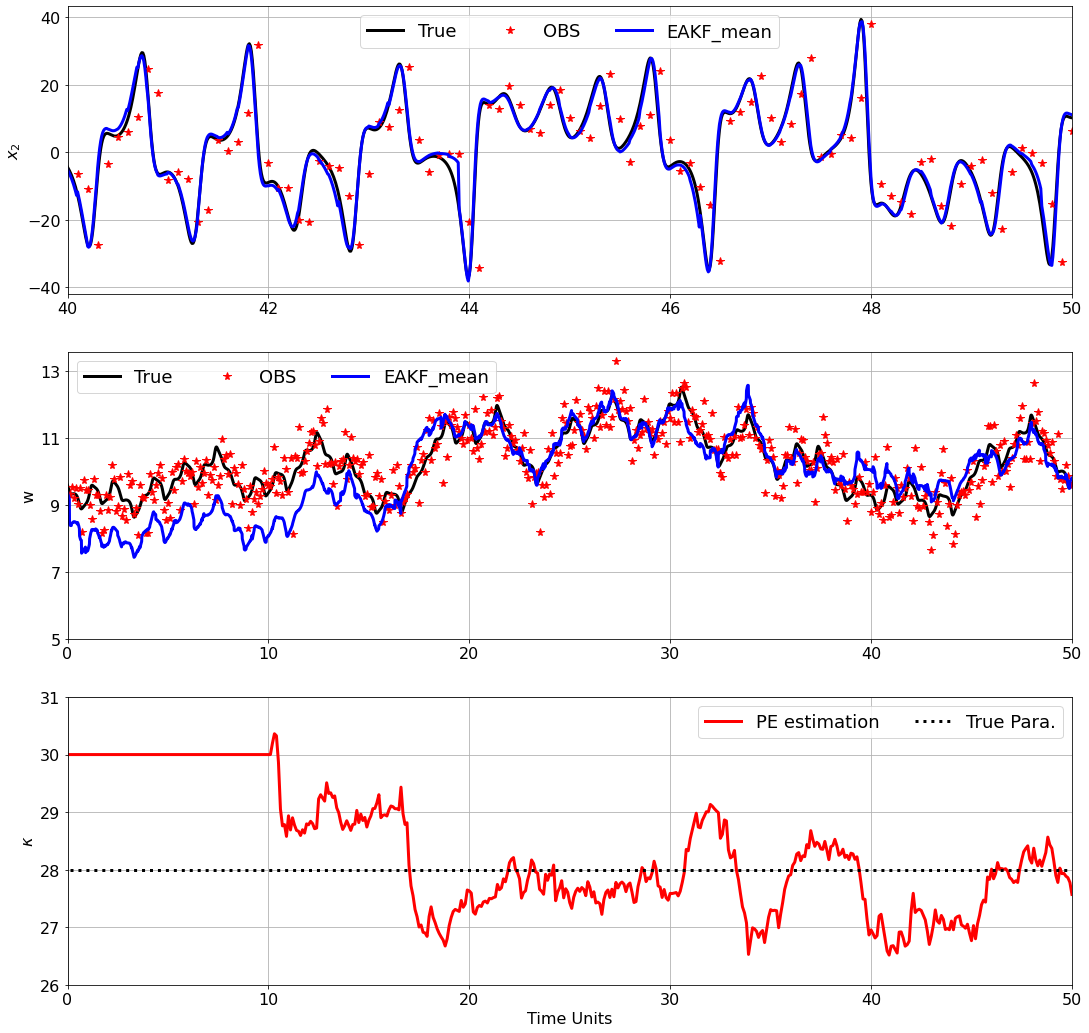
在这里插入图片描述

分析

调整参数估计开始的阶段分别为 0, 1000, 2000, 4000步，发现参数估计开始前，EAKF分析结果与真值存在系统误差，开始参数估计后，EAKF分析结果与真值较为接近，参数很快向参数真值靠拢，在真值附近波动。
调整同化频率为2、5、10、20、50、100，发现随着同化频率的增大，EAKF分析结果与真值的误差越来越大，参数估计值与参数真值距离越来越大，当同化频率为100时，参数估计效果很差，与真值偏离很远。
调整大气观测标准差为0.5、1、2、5，发现当标准差为1时，EAKF分析结果及参数估计结果最为准确，随着观测误差的增大，同化效果变差。当标准差为0.5时，参数估计开始后会经历一段波动期，随后稳定下来，这可能是出现了过拟合的情况。
调整海洋观测标准差为0.5、1、2、5，发现随着观测误差的增大，海洋同化效果变差，参数估计效果变差，但是大气同化效果变化不显著。这表明海洋观测误差标准差主要影响海洋状态变量同化效果，对大气状态变量同化效果影响不明显，这可能是因为海洋的缓慢变化特性。

结论

同化效果对观测数据的频率和质量较为敏感，如果想取得好的同化效果，需要较高的观测频率和观测质量。因此，同化只是一种数据驱动的提高模式精度的手段，我们还应该思考如何提高观测频率和观测质量，以获得更好的模式预报结果。

参考文献

Zhang, Shaoqing, Zhengyu Liu, A. Rosati, and T. Delworth. 2012. “A Study of Enhancive Parameter Correction with Coupled Data Assimilation for Climate Estimation and Prediction Using a Simple Coupled Model.” Tellus A 64:10963.