🍑 算法题解专栏
🍑 题目地址
乔治拿来一组等长的木棒,将它们随机地砍断,使得每一节木棍的长度都不超过 50 50 50 个长度单位。
然后他又想把这些木棍恢复到为裁截前的状态,但忘记了初始时有多少木棒以及木棒的初始长度。
请你设计一个程序,帮助乔治计算木棒的可能最小长度。
每一节木棍的长度都用大于零的整数表示。
输入格式
输入包含多组数据,每组数据包括两行。
第一行是一个不超过 64 64 64 的整数,表示砍断之后共有多少节木棍。
第二行是截断以后,所得到的各节木棍的长度。
在最后一组数据之后,是一个零。
输出格式
为每组数据,分别输出原始木棒的可能最小长度,每组数据占一行。
数据范围
数据保证每一节木棍的长度均不大于 50 50 50。
输入样例:
9
5 2 1 5 2 1 5 2 1
4
1 2 3 4
0
输出样例:
6
5
🍑 剪枝思路
🍤 搜索顺序:对小木棒按照产地古进行降序排序,优先搜索较长的木棒(分支较少)
🍤 可行性剪枝:sum % len == 0 才进行搜索,否则肯定无解
🍤 排除冗余:组合式枚举
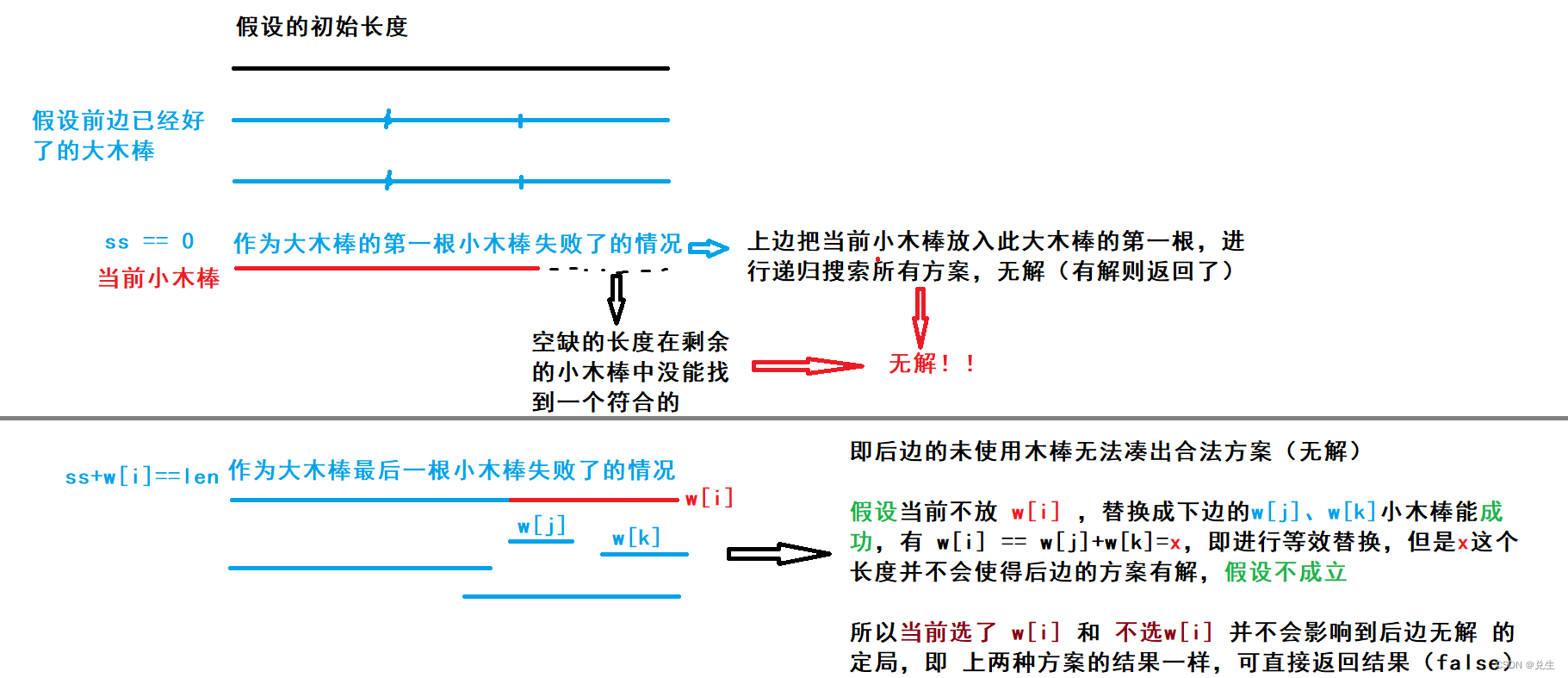
冗余性剪枝
🍑 AC code
import java.util.*;
public class Main
{
static int N = 80, n, sum, len;
static Integer[] w = new Integer[N];// Integer类方便排降序
static boolean[] st = new boolean[N];
/**
* @param u 表示当前已拼成的大木棒根数
* @param ss 表示当前的大木棒长度
* @param start 表示当前已经用到小木棒根数(优化用)
* @return
*/
static boolean dfs(int u, int ss, int start)
{
if (u * len == sum)
return true;
if (ss == len)// 长度等于假设的初始产地古
return dfs(u + 1, 0, 0);
for (int i = start; i < n; i++)
{
if (st[i])
continue;
if (w[i] + ss > len)// 当前小木棒拼接上去就超长了,跳过
continue;
st[i] = true;
if (dfs(u, ss + w[i], i + 1))// 递归搜索
return true;
st[i] = false;// 恢复现场
// 程序执行到这里,说明上面对加入w[i]的尝试都已以失败告终了
// ss == 0 表示这是大木棒的找的第一个小木棒
// 在未使用的木棒中没有一根木棒可以成功的凑成正解的,直接返回
if (ss == 0)
return false;
// w[i]+ss == len:表示当前小木棒是大木棒的最后一根小木棒
// 当前大木棒已经凑好了,但后边的剩余大木棒所有方案都无解,则直接返回无解
if (w[i] + ss == len)
return false;
//当前木棍 i 失败了,那么与它相同长度的也无济于事,也会是失败的,直接跳过省事
int j = i;
while (j < n && w[j] == w[i])// 跳过所有与它相同的木棒
j++;
i = j - 1;// 为什么要 -1 呢,因为待会for循环的i++
}
return false;
}
public static void main(String[] args)
{
Scanner sc = new Scanner(System.in);
while (sc.hasNext())
{
n = sc.nextInt();
if (n == 0)
break;
Arrays.fill(st, false);
sum = 0;
for (int i = 0; i < n; i++)
{
w[i] = sc.nextInt();
sum += w[i];
}
Arrays.sort(w, 0, n, (o1, o2) -> o2 - o1);// Integer数组的降序排序
// Arrays.sort(w, 0, n, (o1, o2) -> Integer.compare(o2, o1));//方式2
for (len = 1; len <= sum; len++)
{
if (sum % len == 0 && dfs(0, 0, 0))
{
System.out.println(len);
break;
}
}
}
}
}