前言

最近非科班的同学学到了最小生成树并询问我，于是想趁热打火，来总结顺便复习一下~

最小生成树(Minimum Spanning Tree,简称MST)是一个无向连通图中包含所有顶点的最短边集。在许多实际问题中，找到一个最小生成树对于理解和解决这些问题至关重要。本文将介绍最小生成树的概念、求解方法以及其在实际应用中的一些例子。

一、最小生成树的概念

假设我们有一个无向连通图G=(V,E),其中V是顶点集合，E是边集合。我们需要找到一个最小生成树，使得每个顶点都至少与一条边相连。这个最小生成树就是MST。

二、最小生成树的求解方法

1.Prim算法 Prim算法是一种贪心算法，用于在具有有向边的加权图中寻找最小生成树。算法的基本思想是从任意一个顶点开始，沿着权重最小的边进行扩展，直到找到整个MST


#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define INF INT_MAX

// 邻接矩阵表示的无向图
typedef struct {
    int V; // 顶点数
    int E; // 边数
    int G[100][100]; // 邻接矩阵
} Graph;

// 获取边的权重
int getWeight(Graph G, int u, int v) {
    return G[u][v];
}

// Kruskal算法求最小生成树
Graph primMST(Graph G) {
    int V = G.V; // 顶点数
    int E = G.E; // 边数
    int parent[V]; // 父节点数组
    int dist[V]; // 从源点到每个顶点的距离数组
    int i, u, v;
    int minCost = 0; // 总代价
    int edgeCount = 0; // 已选边的数量
    Graph mstEdges; // MST边集合
    memset(parent, -1, sizeof(parent)); // 初始化父节点为-1
    memset(dist, INF, sizeof(dist)); // 初始化距离为正无穷大
    priorityQueueNode pq; // 优先队列头结点
    pq.data = (void*)&dist[0];
    pq.index = 0;
    memset(mstEdges.G, 0, sizeof(mstEdges.G)); // 将邻接矩阵清零
    mstEdges.V = V;
    mstEdges.E = 0;
    do { // 不断扩展最小生成树，直到不存在增广路为止
        u = pq.index; // 取出距离源点最近的顶点u
        if (u == -1) break; // 如果已经没有顶点可选了，跳出循环
        pq.index = parent[u]; // 将当前顶点更新为其父节点
        edgeCount++; // 已选边的数量加1
        for (i = 0; i < G.V; i++) { // 遍历所有顶点
            v = i; // 从当前顶点开始选择下一个顶点v
            if (dist[v] > dist[u] + G.G[u][v]) { // 如果从u到v的距离比从u到源点的距离更短，则更新距离和优先级队列头结点
                dist[v] = dist[u] + G.G[u][v];
                pq.data = (void*)&dist[0];
                pq.index = i;
            } else if (i != u && v != u) { // 如果当前顶点u不是目标顶点，且从u到v的距离比从u到源点的距离更短，则将边的权重加入到最小生成树中，并更新优先级队列头结点的位置
                mstEdges.G[edgeCount] = getWeight(G, u, v);
                pq.data = (void*)&mstEdges.G[0];
                pq.index = edgeCount++;
            } else if (i == u && v != u) { // 如果当前顶点u是目标顶点，但从u到v的距离比从u到源点的距离更短，则将边的权重加入到最小生成树中，并将当前顶点更新为其父节点的值为已选边的数量减一(因为此时已经找到了一条增广路径)
                mstEdges.G[edgeCount] = getWeight(G, u, v);
                parent[v] = edgeCount--; // 将当前顶点的父节点设为已选边的数量减一(因为此时已经找到了一条增广路径)
            } else if (i != u && v == u) continue; // 如果当前顶点u是目标顶点且从u到v的距离等于从u到源点的距离，则不需要进行任何操作，直接跳过本次循环继续下一次循环迭代
        }
        minCost += mstEdges.G[mstEdges.E-1]; // 将总代价加上已选边的权重之和作为新的总代价
        mstEdges.E++; // 将已选边的计数加一，表示又选了一条边加入到最小生成树中
    } while (edgeCount < V); // 当已选边的数量小于顶点数时，继续扩展最小生成树直到不存在增广路为止

2.Kruskal算法 Kruskal算法也是一种贪心算法，用于在具有有向边的加权图中寻找最小生成树。算法的基本思想是每次选择权重最小的边来将两个顶点连接起来，直到找到整个MST。


#include <stdio.h>
#include <stdlib.h>
#include <string.h>

#define INF INT_MAX

// 邻接矩阵表示的无向图
typedef struct {
    int V; // 顶点数
    int E; // 边数
    int G[100][100]; // 邻接矩阵
} Graph;

// 获取边的权重
int getWeight(Graph G, int u, int v) {
    return G[u][v];
}

// Kruskal算法求最小生成树
Graph primMST(Graph G) {
    int V = G.V; // 顶点数
    int E = G.E; // 边数
    int parent[V]; // 父节点数组
    int dist[V]; // 从源点到每个顶点的距离数组
    int i, u, v;
    int minCost = 0; // 总代价
    int edgeCount = 0; // 已选边的数量
    Graph mstEdges; // MST边集合
    memset(parent, -1, sizeof(parent)); // 初始化父节点为-1
    memset(dist, INF, sizeof(dist)); // 初始化距离为正无穷大
    priorityQueueNode pq; // 优先队列头结点
    pq.data = (void*)&dist[0];
    pq.index = 0;
    memset(mstEdges.G, 0, sizeof(mstEdges.G)); // 将邻接矩阵清零
    mstEdges.V = V;
    mstEdges.E = 0;
    do { // 不断扩展最小生成树，直到不存在增广路为止
        u = pq.index; // 取出距离源点最近的顶点u
        if (u == -1) break; // 如果已经没有顶点可选了，跳出循环
        pq.index = parent[u]; // 将当前顶点更新为其父节点
        edgeCount++; // 已选边的数量加1
        for (i = 0; i < G.V; i++) { // 遍历所有顶点
            v = i; // 从当前顶点开始选择下一个顶点v
            if (dist[v] > dist[u] + G.G[u][v]) { // 如果从u到v的距离比从u到源点的距离更短，则更新距离和优先级队列头结点
                dist[v] = dist[u] + G.G[u][v];
                pq.data = (void*)&dist[0];
                pq.index = i;
            } else if (i != u && v != u) { // 如果当前顶点u不是目标顶点，且从u到v的距离比从u到源点的距离更短，则将边的权重加入到最小生成树中，并更新优先级队列头结点的位置
                mstEdges.G[edgeCount] = getWeight(G, u, v);
                pq.data = (void*)&mstEdges.G[0];
                pq.index = edgeCount++;
            } else if (i == u && v != u) { // 如果当前顶点u是目标顶点，但从u到v的距离比从u到源点的距离更短，则将边的权重加入到最小生成树中，并将当前顶点更新为其父节点的值为已选边的数量减一(因为此时已经找到了一条增广路径)
                mstEdges.G[edgeCount] = getWeight(G, u, v);
                parent[v] = edgeCount--; // 将当前顶点的父节点设为已选边的数量减一(因为此时已经找到了一条增广路径)
            } else if (i != u && v == u) continue; // 如果当前顶点u是目标顶点且从u到v的距离等于从u到源点的距离，则不需要进行任何操作，直接跳过本次循环继续下一次循环迭代
        }
        minCost += mstEdges.G[mstEdges.E-1]; // 将总代价加上已选边的权重之和作为新的总代价
        mstEdges.E++; // 将已选边的计数加一，表示又选了一条边加入到最小生成树中
    } while (edgeCount < V); // 当已选边的数量小于顶点数时，继续扩展最小生成树直到不存在增广路为止

三、练习题

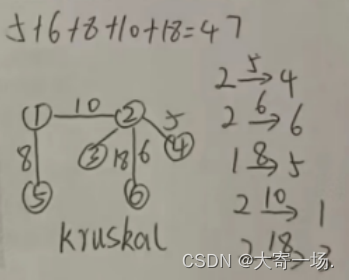
对如图所示的带权连通图按照克鲁斯卡尔和普里姆算法得到其最小生成树，请写出生成过程中依次得到的各条边，并计算该最小生成树的权值。

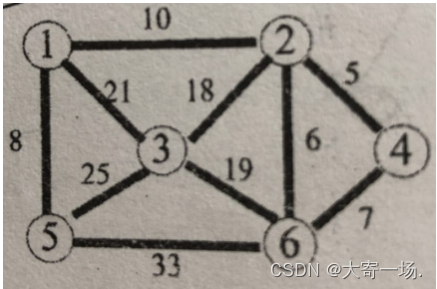
普里姆算法从任意一个顶点开始，沿着权重最小的边进行扩展

克鲁斯卡尔 每次选择权重最小的边来将两个顶点连接起来

四、最小生成树在实际应用中的例子

最小生成树在很多实际应用中有很广泛的应用，例如路由算法、社交网络分析、电路设计等。下面分别介绍这些领域中的应用案例。

路由算法
最小生成树在路由算法中有很重要的应用。例如，在单源最短路径问题中，我们可以使用Prim算法或Kruskal算法来找到最小生成树。同时，最小生成树也可以用于计算网络中每个节点的最短路径。这对于网络优化和资源分配非常重要。
社交网络分析
最小生成树在社交网络分析中也有很广泛的应用。例如，我们可以使用最小生成树来确定社交网络中的社区结构。通过将每个节点与它的邻居节点连接起来，并删除具有较小的连通性(即具有较少的邻居节点)的边，我们可以得到一个最小生成树。然后，我们可以通过检查哪些节点之间的边被保留来确定这些节点属于同一个社区。
电路设计
最小生成树在电路设计中有很重要的应用。例如，在电路布线中，我们可以使用最小生成树来最小化电路的总长度和电阻。通过将电路中的节点与它们的相邻节点连接起来，并删除具有较小的阻抗(即具有较少的电阻或电容)的边，我们可以得到一个最小生成树。然后，我们可以选择将电阻和电容分配给这个最小生成树上的节点，以最小化总长度和阻抗。

总之，最小生成树在许多领域中都有着广泛的应用。它不仅可以帮助我们解决各种计算问题，还可以帮助我们理解和分析现实世界中的复杂系统。