引言

        本系列博客旨在为机器学习(深度学习)提供数学理论基础。因此内容更为精简，适合二次学习的读者快速学习或查阅。

---

1、神经网络优化中的挑战

1.1、病态

        Hessian 矩阵的病态是最难以解决的挑战。将损失函数在点 $x_0$ 处进行二阶泰勒展开，其中 $g$ 是梯度， $H$ 是 Hessian 矩阵：
$$f(x)\approx f(x_0)+(x-x_0{)}^{T}g+\frac{1}{2}(x-x_0{)}^{T}H(x-x_0)$$
        如果将学习率设置为 $ϵ$ ，那么经过梯度下降后新的点 $x=x_0-ϵg$ ，代入上式可得：
$$f(x_0-ϵg)\approx f(x_0)-ϵg^{T}g+\frac{1}{2}{ϵ}^2{g}^{T}Hg$$
        从该式中可以看出，当 $\frac{1}{2}{ϵ}^2{g}^{T}Hg$ 大于 $ϵg^{T}g$ 时，此时即使很小的更新步长也会增加损失函数。这时候梯度的病态问题就凸显出来了，随机梯度下降会“卡”住。
        为了判断病态是否凸显，我们可以在训练过程中，检测每一次学习的平方梯度范数 $g^{T}g$ 和 $g^{T}Hg$ 。在大多数情况下，梯度范数不会在训练过程中显著缩小，但是 $g^{T}Hg$ 的增长会超过一个数量级。
        牛顿法是解决带有病态条件的 Hessian 矩阵的凸优化问题的一个非常优秀的方法，但其在神经网络中却难以应用，原因在 1.3 中进行解释。

1.2、局部极小值

        凸优化问题的一个突出特点是其可以简化为寻找一个局部极小点的问题。任何一个局部极小点都是全局最小点。有些凸函数的底部是一个平坦的区域，而不是单一的全局最小点，但该平坦区域中的任意点都是一个可以接受的解。优化一个凸问题时，若发现了任何形式的临界点，我们都会知道已经找到了一个不错的可行解。
        对于非凸函数时，如神经网络，有可能会存在多个局部极小值。事实上，几乎所有的深度模型基本上都会有非常多的局部极小值。然而，我们会发现这并不是主要问题。
        模型可辨识性：如果一个足够大的训练集可以唯一确定一组模型参数，那么该模型被称为可辨认的。
        而神经网络和任意具有多个等效参数化潜变量的模型通常是不可辨认的，因为通过相互交换潜变量我们能得到等价的模型。例如，考虑神经网络的第一层，我们可以交换单元 $i$ 和单元 $j$ 的传入权重向量、传出权重向量而得到等价的模型。如果神经网络有 $m$ 层，每层有 $n$ 个单元，那么会有 $n{!}^m$ 种排列隐藏单元的方式。这种不可辨认性被称为权重空间对称性。
        除了权重空间对称性，很多神经网络还有其他导致不可辨认的原因。例如，在任意整流线性网络或者 maxout 网络中，我们可以将传入权重和偏置扩大 $\alpha$ 倍，然后将传出权重扩大 $\frac{1}{\alpha }$ 倍，而保持模型等价。这意味着，如果代价函数不包括如权重衰减这种直接依赖于权重而非模型输出的项，那么整流线性网络或者 maxout 网络的每一个局部极小点都在等价的局部极小值的 $（m\times n)$ 维双曲线上。
        这些模型可辨识性问题意味着，神经网络代价函数具有非常多甚至无限多的局部极小值。然而，所有这些由于不可辨识性问题而产生的局部极小值都有相同的代价函数值。因此，这些局部极小值并非是非凸所带来的问题。
        如果局部极小值相比全局最小点拥有很大的代价，局部极小值会带来很大的隐患。我们可以构建没有隐藏单元的小规模神经网络，其局部极小值的代价比全局最小点的代价大很多。如果具有很大代价的局部极小值是常见的，那么这将给基于梯度的优化算法带来极大的问题。
        对于实际中感兴趣的网络，是否存在大量代价很高的局部极小值，优化算法是否会碰到这些局部极小值，都是尚未解决的公开问题。多年来，大多数从业者认为局部极小值是困扰神经网络优化的常见问题。如今，情况有所变化。这个问题仍然是学术界的热点问题，但是学者们现在猜想，对于足够大的神经网络而言，大部分局部极小值都具有很小的代价函数，我们能不能找到真正的全局最小点并不重要，而是需要在参数空间中找到一个代价很小（但不是最小）的点。
        一种能够检测局部极小值是否为主要问题的检测方法是：画出梯度范数随时间的变化。如果梯度范数没有缩小到一个微小的值，那么该问题既不是局部极小值，也不是其他形式的临界点。在高维空间中，很难明确证明局部极小值是导致问题的原因。许多并非局部极小值的结构也具有很小的梯度。

1.3、高原、鞍点和其它平坦区域

        对于很多高维非凸函数而言，局部极小值（以及极大值）都远少于另一类梯度为零的点：鞍点。鞍点附近的某些点比鞍点有更大的代价，而其他点则有更小的代价。在鞍点处，Hessian 矩阵同时具有正负特征值。位于正特征值对应的特征向量方向的点比鞍点有更大的代价，反之，位于负特征值对应的特征向量方向的点有更小的代价。我们可以将鞍点视为代价函数某个横截面上的局部极小点，同时也可以视为代价函数某个横截面上的局部极大点。
        多类随机函数表现出以下性质：
        （1）低维空间中，局部极小值很普遍。但在更高维空间中，局部极小值很罕见，而鞍点则很常见。
        （2）当我们到达代价较低的区间时，Hessian 矩阵的特征值为正的可能性更大。也就是意味着，局部极小值具有低代价的可能性比高代价要大得多。具有高代价的临界点更有可能是鞍点。具有极高代价的临界点就很可能是局部极大值了。
        鞍点激增对于训练算法来说有哪些影响呢？对于只使用梯度信息的一阶优化算法而言，目前情况还不清楚。有实验表明，梯度下降似乎可以在许多情况下逃离鞍点，但对梯度下降更现实的使用场景来说，情况可能会有所不同。但对于牛顿法而言，鞍点显然是一个问题。梯度下降旨在朝“下坡”移动，而非明确寻求临界点。而牛顿法的目标是寻求梯度为零的点。如果没有适当的修改，牛顿法就会跳进一个鞍点。高维空间中鞍点的激增或许解释了在神经网络训练中为什么二阶方法无法成功取代梯度下降。
        除了极小值和鞍点，还存在其他梯度为零的点。例如从优化的角度看与鞍点很相似的极大值，很多算法不会被吸引到极大值，除了未经修改的牛顿法。和极小值一样，许多种类的随机函数的极大值在高维空间中也是指数级稀少。
        也可能存在恒值的、宽且平坦的区域。在这些区域，梯度和 Hessian 矩阵都是零。这种退化的情形是所有数值优化算法的主要问题。在凸问题中，一个宽而平坦的区间肯定包含全局极小值，但是对于一般的优化问题而言，这样的区域可能会对应着代价函数中一个较高的值。

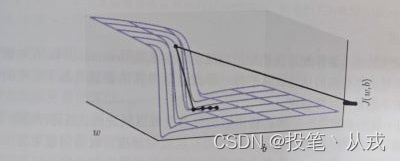
1.4、悬崖

        多层神经网络通常存在像悬崖一样的斜率较大区域，如下图所示。这是由于几个较大的权重相乘导致的。遇到斜率极大的悬崖结构时，梯度更新会很大程度地改变参数值，通常会完全跳过这类悬崖结构。
        不管我们是从上还是从下接近悬崖，情况都很糟糕，但幸运的是，我们可以使用启发式梯度截断来避免其严重的后果。其基本想法源自梯度并没有指明最佳步长，只说明了在无限小区域内的最佳方向。当传统的梯度下降算法提议更新很大一步时，启发式梯度截断会干涉来减小步长，从而使其不太可能走出梯度近似为最陡下降方向的悬崖区域。悬崖结构在循环神经网络的代价函数中很常见，因为这类模型会涉及多个因子的相乘，其中每个因子对应一个时间步。
        

1.5、长期依赖、梯度消失与梯度爆炸

        当计算图变得极深时，神经网络优化算法会面临的另一个难题就是长期依赖问题----由于变深的结构使模型丧失了学习到先前信息的能力，让优化变得极其困难。深层的计算图不仅存在于前馈网络，还存在于循环网络中。因为循环网络要在很长时间序列的各个时刻重复应用相同操作来构建非常深的计算图，并且模型参数共享，这使问题更加凸显。
        例如，假设某个计算图中包含一条反复与矩阵 $W$ 相乘的路径。那么 $t$ 步后，相当于乘以 $W^t$ 。假设 $W$ 有特征值分解 $W=Vdiag(\lambda )V^{-1}$ ，有：
$$W^t=(Vdiag(\lambda )V^{-1}{)}^t=Vdiag(\lambda {)}^t{V}^{-1}$$
        从上式中可以看出，当特征值 ${\lambda }_i$ 大于 1 时会梯度爆炸；小于 1 时则会梯度消失。梯度消失使得我们难以知道参数朝哪个方向移动能够改进代价函数，而梯度爆炸会使得学习不稳定。悬崖结构便是梯度爆炸现象的一个例子。
        循环网络在各时间步上使用相同的矩阵 $W$ ，而前馈网络并没有。所以即使使用非常深层的前馈网络，也能很大程度上有效地避免梯度爆炸与梯度消失问题。

1.6、非精确梯度

        在梯度计算过程中，由于时间、存储和计算能力等限制，无法获得完全精确的梯度值。为了缩短计算时间或减小计算资源消耗，常常采用非精确梯度计算方法，从而使梯度下降算法能够在更短的时间内找到较优解。

1.7、局部和全局结构间的弱对应

        如果梯度方向在局部改进很大，但并没有指向代价低得多的遥远区域，那么我们有可能在单点处克服上述所有困难，但仍然表现不佳。
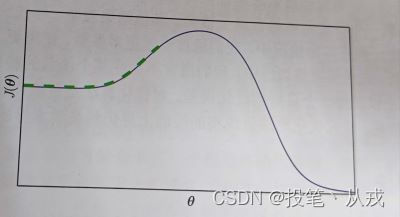
        大多数优化研究的难点集中于训练是否找到了全局最小点、局部极小点或是鞍点，但在实践中神经网络不会到达任何一种临界点。甚至，这些临界点不一定存在。例如，损失函数 $-\log p(y|x;\theta )$ 可以没有全局最小点，而是当随着训练模型逐渐稳定后，渐近地收敛于某个值。如下图所示，即使没有局部极小值和鞍点，该例还是不能从局部优化中找到一个良好的代价函数值。
        我们需要进一步探索影响学习轨迹长度和更好地表征训练过程的结果。
        许多现有研究方法在求解具有困难全局结构的问题时，旨在寻求良好的初始点，而不是开发非局部范围更新的算法。
        梯度下降和基本上所有的可以有效训练神经网络的学习算法，都是基于局部较小更新，而这可能导致训练时间过长。如下图所示，在高维空间中，学习算法通常可以环绕过这样的高山，但是相关轨迹可能会很长，进一步导致训练时间过长。
        有时，比如说当目标函数有一个宽而平的区域，或是我们试图寻求精确的临界点（通常来说后一种情况只发生于显式求解临界点的方法，如牛顿法）时，局部信息不能为我们提供任何指导。在这些情况下，局部下降完全无法定义通向解的路径。在其他情况下，局部移动可能太过贪心，朝着下坡方向移动，却和所有可行解南辕北辙，或者是用舍近求远的方法来求解问题。目前，我们还不了解这些问题中的哪一个与神经网络优化中的难点最相关。但不管哪个问题最重要，如果存在一个区域，我们遵循局部下降便能合理地直接到达某个解，并且我们能够在该良好区域上初始化学习，那么这些问题都可以避免。
        最终的观点还是建议在传统优化算法上研究怎样选择更佳的初始化点，以此来实现目标更切实可行。
        

1.8、优化的理论限制

        有研究表明，我们为神经网络设计的任何优化算法都有性能限制。寻找给定规模的网络的一个可行解是很困难的，但在实际情况中，我们可以通过设置更多的参数，使用更大的网络，能轻松找到可接受的解。

2、优化算法

        本节中只介绍优化算法相关的性质和简介，并不涉及实现原理。

2.1、随机梯度下降（SGD）

        随机梯度下降（SGD）及其变种是深度学习中应用最多的优化算法。SGD 算法中的一个关键参数是学习率。学习率可以通过实验和误差来选取，通常最好的选择方法是检测损失函数值随时间变化的学习曲线。如果学习曲线剧烈震荡，则学习率设置过大。如果学习率设置的过小，又会导致学习过程过于缓慢，甚至会卡在一个相当高的损失值处。因此我们需要不断地调整学习率，让学习曲线具有温和的震荡。在实践中，我们通常会让学习率随着时间的推移逐渐降低， $N$ 步之后变成一个更小的常数，从而保证 SGD 收敛。
        SGD 及相关的小批量亦或更广义的基于梯度优化的在线学习算法，一个重要的性质是每一步更新的计算时间不依赖训练样本数目的多寡。即使训练样本数目非常大时，它们也能收敛。对于足够大的数据集，SGD 可能会在处理完整个训练集之前就收敛到最终测试集误差的某个固定容差范围内。

2.2、动量

        虽然随机梯度下降仍然是非常受欢迎的优化方法，但其学习过程有时会很慢。动量方法旨在加速学习，特别是处理高曲率、小但一致的梯度，或是带噪声的梯度。动量算法累积了之前梯度指数级衰减的移动平均，并且继续沿该方向移动。
        动量的主要目的是解决两个问题：Hessian 矩阵的病态条件和随机梯度的方差。

2.3、Nesterov 动量

        是动量算法的一个变种，和标准动量之间的区别体现在梯度计算上。Nesterov 动量中，梯度计算在施加当前速度之后。因此，Nesterov 动量可以解释为往标准动量方法中添加了一个校正因子。

2.4、AdaGrad

        能够独立地适应所有模型参数的学习率，缩放每个参数反比于其所有梯度历史平方值总和的平方根。具有损失最大偏导的参数相应地有一个快速下降的学习率，而具有小偏导的参数在学习率上有相对较小的下降。净效果是在参数空间中更为平缓的倾斜方向会取得更大的进步。
        然而，实践中发现，对于训练深度神经网络而言，从训练开始时积累梯度平方会导致有效学习率过早和过量的减小，因此效果不佳。

2.5、RMSProp

        RMSProp 算法修改 AdaGrad 以在非凸设定下效果更好，改变梯度积累为指数加权的移动平均。AdaGrad 旨在应用于凸问题时快速收敛。当应用于非凸函数训练神经网络时，学习轨迹可能穿过了很多不同的结构，最终到达一个局部是凸碗的区域。AdaGrad 根据平方梯度的整个历史收缩学习率，可能使得学习率在达到这样的凸结构前就变得太小了。RMSProp 使用指数衰减平均以丢弃遥远过去的历史，使其能够在找到凸碗状结构后快速收敛，它就像一个初始化于该碗状结构的 AdaGrad 算法实例。
        实践表明，RMSProp是一种有效且实用的深度神经网络优化算法，是经常采用的优化方法之一。

2.6、Adam

        “Adam” 这个名字派生自短语 “adaptive moments”。早期算法背景下，它也许最好被看作结合 RMSProp 和具有一些重要区别的动量的变种。首先，在 Adam 中，动量直接并入了梯度一阶矩（指数加权）的估计。将动量加入 RMSProp 最直观的方法是将动量应用于缩放后的梯度。结合缩放的动量使用没有明确的理论动机。其次，Adam包括偏置修正，修正从原点初始化的一阶矩（动量项）和（非中心的）二阶矩的估计。RMSProp 也采用了（非中心的）二阶矩估计，然而缺失了修正因子。因此，不像 Adam，RMSProp 二阶矩估计可能在训练初期有很高的偏置。Adam 通常被认为对超参数的选择相当鲁棒，尽管学习率有时需要从建议的默认修改。

2.7、小结

        虽然优化算法有很多，但是有实验表明，在大量学习任务上，似乎没有哪个算法能够脱颖而出。即使是最简单的 SGD，也未必就比 Adam 效果要差。因此，选择哪一个优化算法主要取决于使用者对算法的熟悉程度，以便调节超参数。

3、参数初始化策略

        参数初始化必须在不同单元间“破坏对称性”，即需要具有不同的初始参数，否则这些单元不管怎么更新，都将具有相同的权重，成为冗余单元。我们通常会将偏置项设置为启发式挑选的常数，仅随机初始化权重，额外的参数通常和偏置一样设置为启发式的常数。目前最常用的权重初始化策略是高斯分布初始化和均匀分布初始化，并且初始分布的大小和范围对优化过程和泛化能力具有很大的影响。
        更大的初始权重具有更强的破坏对称性的作用，有助于避免冗余单位。它们也有助于避免在每层线性成分的前向或后向传播中丢失信号----矩阵中更大的值在矩阵乘法中有更大的输出。但如果初始权重过大，那么会在前向传播或反向传播中产生爆炸的值。较大的权重也会产生使得激活函数饱和的值，导致饱和单元的梯度完全丢失。
        如果可以的话，最好将每层权重的初始数值范围设为超参数。是否选择使用密集或稀疏初始化也可以设为一个超参数。一个好的挑选初始数值范围的经验法则是观测单个小批量数据上的激活或梯度的幅度或标准差。如果权重太小，那么当激活值在小批量上前向传播于网络时，激活值的幅度会缩小。通过重复识别具有小得不可接受的激活值的第一层，并提高其权重，最终有可能得到一个初始激活全部合理的网络。如果学习在这点上仍然很慢，观测梯度的幅度或标准差可能也会有所帮助。
        设置偏置的方法必须和设置权重的方法协调。大多数情况下可以将偏置设为零，但也存在一些设置偏置非零值的情况：
        1）如果偏置是作为输出单元，那么初始化偏置以获取正确的输出边缘统计通常是有利的。要做到这一点，我们假设初始权重足够小，该单元的输出仅由偏置决定。这说明设置偏置为应用于训练集上输出边缘统计的激活函数的逆。例如，如果输出是类上的分布，且该分布是高度偏态分布，第 $i$ 类的边缘概率由某个向量 $c$ 的第 $i$ 个元素给定，那么我们可以通过求解方程 $softmax(b)=c$ 来设置偏置向量 $b$ 。这不仅适用于分类器，也适用于如自编码器和尔兹曼机等模型。这些模型拥有输出类似于输入数据 $x$ 的网络层，非常有助于初始化这些层的偏置以匹配 $x$ 上的边缘分布。
        2）有时，我们可能想要选择偏置以避免初始化引起太大饱和。例如，我们可能会将 ReLU 的隐藏单元设为 0.1 而非 0，以避免 ReLU 在初始化时饱和。尽管这种方法违背不希望偏置具有很强输入的权重初始化准则。例如，不建议使用随机游走初始化。
        3）有时，一个单元会控制其他单元能否参与到等式中。在这种情况下，我们有一个单元输出 $u$ ，另一个单元 $h\in [0,1]$ ，那么我们可以将 $h$ 视作门，以决定 $uh\approx 1$ 还是 $uh\approx 0$ 。在这种情形下，我们希望设置偏置 $h$ ，使得在初始化的大多数情况下 $h\approx 1$ 。否则， $u$ 没有机会学习。例如，Jozefowicz 提议设置 LSTM 模型遗忘门的偏置为 1。
        除了这些初始化模型参数的简单常数或随机方法，还有可能使用机器学习初始化模型参数。一个常用策略是使用相同的输入数据集，用无监督模型训练出来的参数来初始化监督模型。我们也可以在相关问题上使用监督训练。即使是在一个不相关的任务上运行监督训练，有时也能得到一个比随机初始化具有更快收敛率的初始值。这些初始化策略有些能够得到更快的收敛率和更好的泛化误差，因为它们编码了模型初始参数的分布信息。