文章目录
- 什么是迷宫问题?
- 如何解决迷宫问题?
- DFS(深度优先搜索)
- BFS(广度优先搜索)
- 总结
什么是迷宫问题?
迷宫问题是一道经典的算法问题,旨在寻找一条从起点到终点的最短路径。通常迷宫由一个二维矩阵表示,其中0代表可通过的空地,1代表墙壁不可通过。
在此条件下,需要运用数据结构中的图算法如广度优先搜索(BFS)或深度优先搜索(DFS)等找出一条从起点到终点的最短路径。
- 例如,以下就是一个迷宫:
111111111111111
100010001000001
101110101011001
100000101000101
111110111010101
100000001010101
101111111010101
101000001010001
101111101110101
100010000000101
111110111110101
100000100000101
111110101011101
100000001000001
111111111111111
(其中1表示墙壁不可通过,0表示可以通过的路径。起点为(1,1),终点为(15,15))
如何解决迷宫问题?
DFS(深度优先搜索)
对于深搜的基础知识,可以看我之前的博客:【算法基础】深搜
- 使用深度优先搜索(DFS)算法来解决迷宫问题。具体思路如下:
- 选定起点,建立一个 visited 数组记录每个点是否已经遍历过。
- 对于起点开始向四周探索,如果能够到达未曾遍历的点,则继续向该点前进,直到无法前进或者到达出口。
- 在探索的过程中,将每个点的状态更新到visited数组中并标记已经访问。
- 如果走到了出口,则找到了一条可行路径;否则回溯到上一个节点分别从其它方向继续探索,直到所有状态被访问。
但是,深搜并不适合解决迷宫问题,甚至有时得到的解是错误的。
在实现时需要注意,DFS 算法虽然容易理解和实现,但是存在回溯次数多、时间复杂度高等缺点。因此,在实际应用中,需要仔细考虑算法的时间复杂度,并选择合适的数据结构和优化手段来提高程序效率。
-
下面来看一个错误的案例:
用二维数组来表示迷宫,每个元素表示该位置上的状态(例如墙壁、通道等)。其中,’O’表示可到达点,’X’表示不可到达点,’S’表示起始点,’E’表示终点。 -
首先,初始数组的文件是这样的:

-
最短路径显然是从S直接到E,一步就可以解决问题,但事实是dfs走了27步。。。
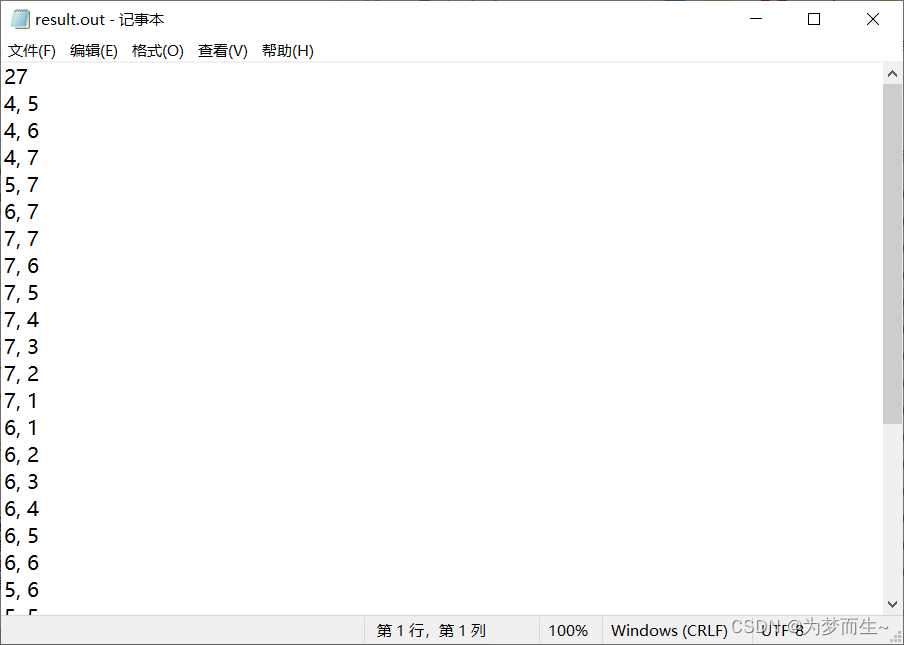
因为dfs的代码是这样的:
//ei, ej表示终点坐标,si, sj表示起点坐标,i, j表示现在的坐标
int dfs(int ei, int ej, int si, int sj, int i, int j){
int flag = 0; //标记是否到达终点
a[i][j] = '.'; //标记此位置,表示已经访问过
if(i == ei && j == ej){
flag = 1;
if(cnt <= min_cnt) min_cnt = cnt;
}
//往右
if(flag != 1 && j+1 <= n && (a[i][j+1] == 'O' || a[i][j+1] == 'E')){
push(s, i, j);
if(dfs(ei ,ej, si, sj, i, j+1)==1){
cnt++;
flag = 1;
}
}
//往下
if(flag != 1 && i+1 <= m && (a[i+1][j] == 'O' || a[i+1][j] == 'E')){
push(s, i, j);
if(dfs(ei, ej, si, sj, i+1, j) == 1){
cnt++;
flag = 1;
}
}
//往左
if(flag != 1 && j-1 > 0 && (a[i][j-1] == 'O' || a[i][j-1] == 'E')){
push(s, i, j);
if(dfs(ei, ej, si, sj, i, j-1) == 1){
cnt++;
flag = 1;
}
}
//往上
if(flag != 1 && i-1 > 0 && (a[i-1][j] == 'O' || a[i-1][j] == 'E')){
push(s, i, j);
if(dfs(ei, ej, si, sj, i-1, j) == 1){
cnt++;
flag = 1;
}
}
if(flag != 1){
a[i][j] == 'O';
pop(s);
cnt--;
}
return flag;
}
并没有找到最短路径,而是按照程序既定的顺序寻找终点。当然,我们也可以完善以下程序使寻路变得更加只能,但是这样写出来代码过于复杂。
BFS(广度优先搜索)
与BFS不同,BFS 算法的基本思路是从起点开始进行多层级别的搜索,逐渐向外扩展,直到找到终点或者所有状态被访问为止。
- 具体步骤如下:
- 选定起点,以其为根节点建立一个 BFS 树,将其压入队列中。
- 对于每个节点,枚举所有可走的方向,生成该节点的子节点,并将其加入队列尾部。
- 在生成子节点时需要判断是否合法,如果不合法则忽略。这里建议使用 visited 数组记录每个点是否已经遍历过,以免出现死循环。
- 每次从队列头部取出一个节点并访问,直到队列为空或找到终点。
- 最终,如果想要打印出从起点到终点的路径,需要用到栈和BFS相配合。
- 实现链栈的基本操作:栈在本实验中用于记录解决迷宫的路径,要实现基本的初始化、入栈、出栈和判空等操作。
- 实现链式队列的基本操作:bfs算法借助队列实现迷宫路径的查找,所以要实现基本的初始化、入队、出队等操作。
BFS 算法不需要使用递归函数,因此比起 DFS 更容易实现和调试,并且可以找到最短路线。但是其空间复杂度较高,因此在实际应用中需要注意算法效率和内存占用情况。
其次,BFS算法是同时向外扩展多个路径,每一次扩展时,每一条路径都是相同的步数,所以首先到达终点的那条路径一定是步数最少的,也就是最短路径。
同样使用上面的迷宫表示方法,我们来看一下BFS的代码和性能:
// bfs算法,求出从起点到终点的最短路径,并输出路径中每一个点的坐标
int bfs(Point start, Point end) {
Queue queue;
initQueue(&queue);
enQueue(&queue, start);
vis[start.x][start.y] = 1;
//bfs
while (queue.front != NULL) {
Point current = deQueue(&queue);
//已经到达终点
if (isEndPoint(maze, current)) {
showPath(current, start, end);
return 1;
}
// 上下左右四个方向搜索可达点
Point up = {current.x - 1, current.y};
Point down = {current.x + 1, current.y};
Point left = {current.x, current.y - 1};
Point right = {current.x, current.y + 1};
//向上
if (up.x > 0 && isAccessible(maze, up) && !vis[up.x][up.y]) {
enQueue(&queue, up);
vis[up.x][up.y] = current.x * MAX_LEN + current.y;
}
//向下
if (down.x <= m && isAccessible(maze, down) && !vis[down.x][down.y]) {
enQueue(&queue, down);
vis[down.x][down.y] = current.x * MAX_LEN + current.y;
}
//向左
if (left.y > 0 && isAccessible(maze, left) && !vis[left.x][left.y]) {
enQueue(&queue, left);
vis[left.x][left.y] = current.x * MAX_LEN + current.y;
}
//向右
if (right.y <= n && isAccessible(maze, right) && !vis[right.x][right.y]) {
enQueue(&queue, right);
vis[right.x][right.y] = current.x * MAX_LEN + current.y;
}
}
printf("Error: no path found!\n");
return 0;
}
具体代码可以从这里下载:
初始迷宫是这样的:
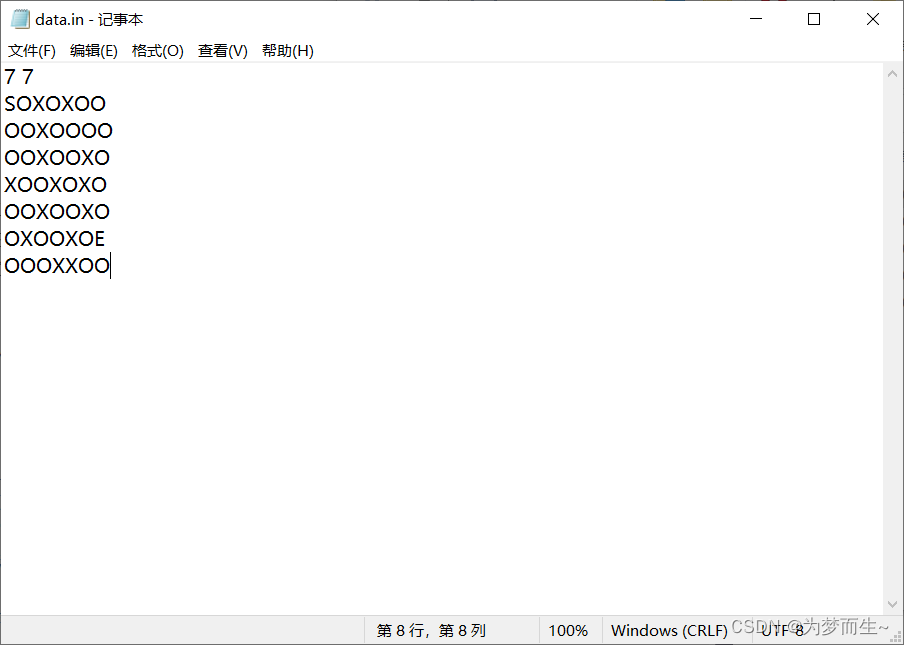
可以找到最短路径并输出:
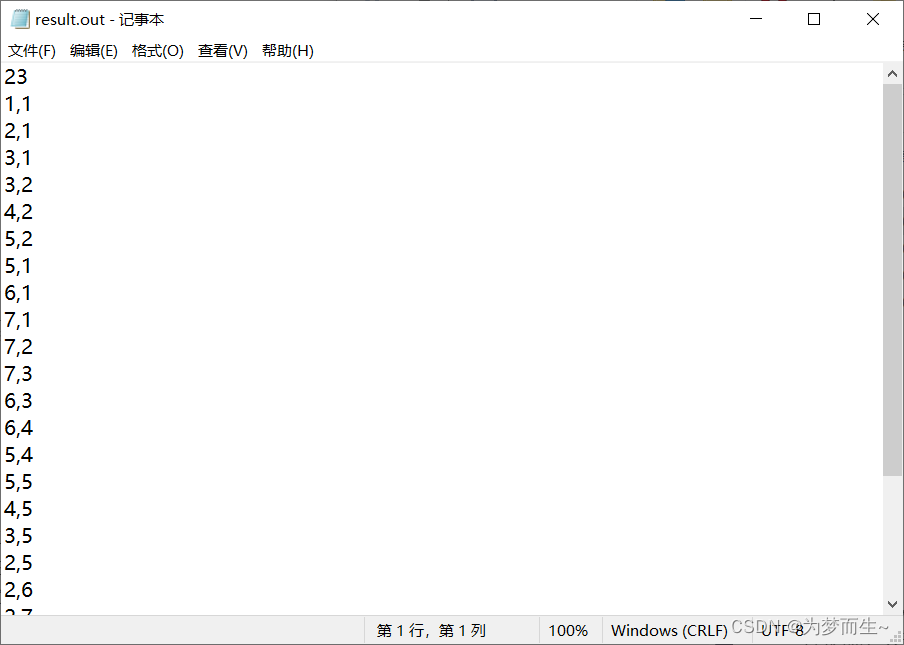
如果需要以上的全部代码可以看本博客上传的代码包。
总结
迷宫问题是求解从起点到终点的路径,使得路径能够遍历迷宫所有有效格子的问题。这个问题在计算机科学中被广泛研究,有很多种算法可以解决。
-
在深度优先搜索(DFS)算法中,我们需要递归地向前探索,直到找到终点或无法继续前进为止。DFS 算法比较容易实现,但是可能会导致出现死循环和非最优解。
-
广度优先搜索(BFS)算法则采用分层扩展的方式,从起点开始进行多层级别的搜索,逐渐向外扩展,直到找到终点或者所有状态被访问为止。BFS 算法能够找到最短路径,并且不会出现死循环的情况,但是空间复杂度比 DFS 更高。
另外,A* 算法是一种启发式搜索算法,也可以很好的解决迷宫问题。它是基于估价函数对每个节点的代价进行评估,并根据代价来选择下一个扩展的节点。使用 A* 算法可以更快地找到最短路径,但是需要设计合适的估价函数。
除此之外,还有其他一些算法,如Dijkstra算法、IDA*算法等,均有自己的特点和应用场景。