【刷题之路Ⅱ】LeetCode 1823. 找出游戏的获胜者
- 一、题目描述
- 二、解题
- 1、方法1——单向环形链表
- 1.1、思路分析
- 1.2、代码实现
- 2、方法2——队列
- 2.1、思路分析
- 2.2、先将队列实现一下
- 2.3、代码实现
一、题目描述
原题连接: 1823. 找出游戏的获胜者
题目描述:
共有 n 名小伙伴一起做游戏。小伙伴们围成一圈,按 顺时针顺序 从 1 到 n 编号。确切地说,从第 i 名小伙伴顺时针移动一位会到达第 (i+1) 名小伙伴的位置,其中 1 <= i < n ,从第 n 名小伙伴顺时针移动一位会回到第 1 名小伙伴的位置。
游戏遵循如下规则:
从第 1 名小伙伴所在位置 开始 。
沿着顺时针方向数 k 名小伙伴,计数时需要 包含 起始时的那位小伙伴。逐个绕圈进行计数,一些小伙伴可能会被数过不止一次。
你数到的最后一名小伙伴需要离开圈子,并视作输掉游戏。
如果圈子中仍然有不止一名小伙伴,从刚刚输掉的小伙伴的 顺时针下一位 小伙伴 开始,回到步骤 2 继续执行。
否则,圈子中最后一名小伙伴赢得游戏。
给你参与游戏的小伙伴总数 n ,和一个整数 k ,返回游戏的获胜者。
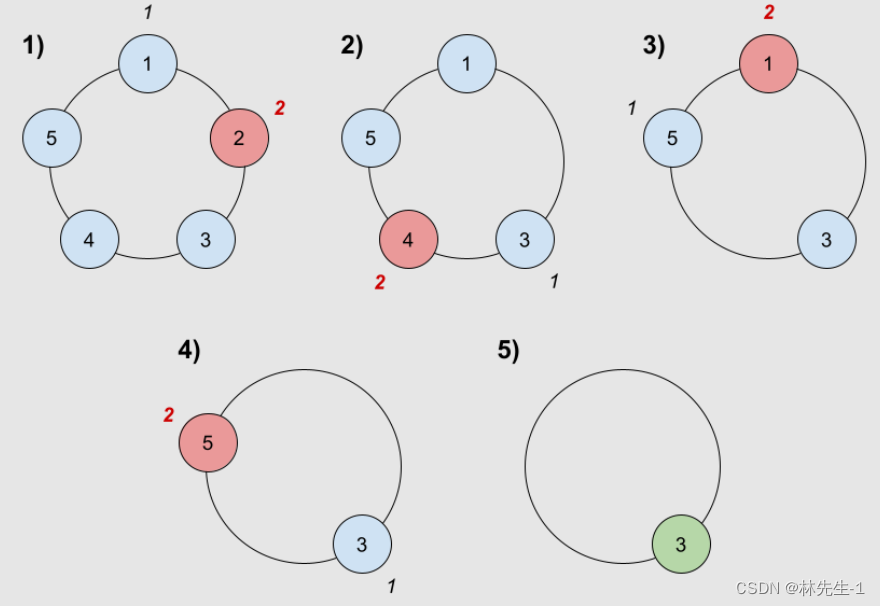
示例 1:
输入: n = 5, k = 2
输出: 3
解释:游戏运行步骤如下:
- 从小伙伴 1 开始。
- 顺时针数 2 名小伙伴,也就是小伙伴 1 和 2 。
- 小伙伴 2 离开圈子。下一次从小伙伴 3 开始。
- 顺时针数 2 名小伙伴,也就是小伙伴 3 和 4 。
- 小伙伴 4 离开圈子。下一次从小伙伴 5 开始。
- 顺时针数 2 名小伙伴,也就是小伙伴 5 和 1 。
- 小伙伴 1 离开圈子。下一次从小伙伴 3 开始。
- 顺时针数 2 名小伙伴,也就是小伙伴 3 和 5 。
- 小伙伴 5 离开圈子。只剩下小伙伴 3 。所以小伙伴 3 是游戏的获胜者。
示例 2:
输入: n = 6, k = 5
输出: 1
解释:小伙伴离开圈子的顺序:5、4、6、2、3 。小伙伴 1 是游戏的获胜者。
提示:
1 <= k <= n <= 500
进阶:你能否使用线性时间复杂度和常数空间复杂度解决此问题?
二、解题
1、方法1——单向环形链表
1.1、思路分析
正如题目所描述的一样,我们可以让小伙伴们形成一个环,然后从第一个小伙伴开始数k个数,数到第k个小伙伴的时候就将其出队。
非常形象地,我们可以用一个单向循环链表来解决这个问题,起初我们要先创建出一个循环表链:
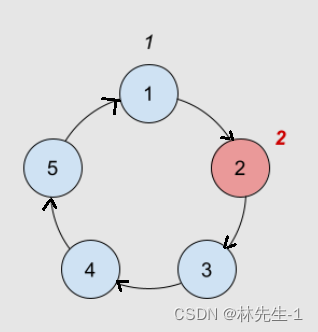
当k大于1时,我们用一个cur指针指向第一个节点,然后让cur往后走k - 1步,然后删除一个节点。然后从被删除节点的下一个节点开始在重复上述过程,直到链表中只剩下一个节点,剩下的这一个节点就是胜利者,我们返回他的序号即可。
因为是单链表,所以我们还需要另外一个指针pre,来保存被删除节点的上一个节点,以辅助删除后再连接成环:
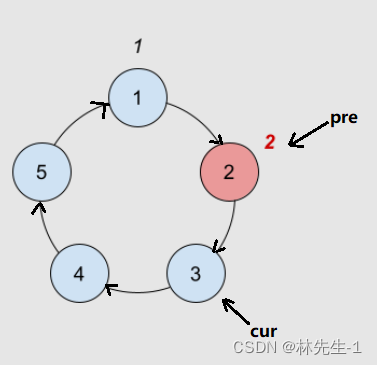
相信这已经是链表的基本操作了,大家应该都能掌握。
而当k等于1时,问题就变得非常简单了,此时的问题就变成依次删除链表中的节点,直到只剩下一个节点。
1.2、代码实现
有了以上思路,那我们写起代码来也就水到渠成了:
// 先定义环形链表节点
typedef struct circleListNode {
int id;
struct circleListNode *next;
} cirNode;
int findTheWinner(int n, int k) {
// 先创建好环形链表
int i = 0;
cirNode *head = NULL; // 保存第一个节点
cirNode *tail = NULL; // 保存最后一个节点
for (i = 1; i <= n; i++) {
cirNode *newNode = (cirNode*)malloc(sizeof(cirNode));
if (NULL == newNode) {
perror("malloc fail!\n");
exit(-1);
}
newNode->id = i;
if (1 == i) {
head = newNode;
tail = newNode;
} else {
tail->next = newNode;
tail = tail->next;
}
}
// 连接成环
tail->next = head;
cirNode *cur = head;
cirNode *pre = cur; // 保存被删除节点的前一个节点
while (n > 1) {
if (k > 1) {
for (i = 0; i < k - 1; i++) {
pre = cur;
cur = cur->next;
}
pre->next = cur->next;
free(cur);
cur = pre->next;
} else {
cirNode *next = cur->next;
free(cur);
cur = next;
}
n--;
}
int winner = cur->id;
free(cur);
return winner;
}
时间复杂度:O(nk),初始时我们要创建单向环形链表,复杂度为O(n)。每一轮我们都要让cur移动k - 1次,重复到链表中只剩1个节点,故需要重复n - 1次,故此操作的复杂为O(nk)。故总的时间复杂度为O(nk)。
空间复杂度:O(n),我们需要n个链表节点连接成环,故空间复杂度为O(n)。
2、方法2——队列
2.1、思路分析
其实我们也可以用一个非循环队列来模拟出一个循环队列,模拟的方法也很简单,我们每次都让队头元素再排到队尾,因为队列的先进先出的规则,这样模拟的结果很好的符合了循环遍历的结果。
所以我们先将小伙伴们全都入队,完事后对头元素就是序号为1的小伙伴。
然后我们从对头元素开始,依次将队头元素移动到队尾,执行k - 1次,然后再将对头元素出队。
重复上述过程,直到队列中只剩一个元素,剩下的就是胜利者,我们返回其序号即可。
2.2、先将队列实现一下
先将队列CV一下:
// 重定义数据类型
typedef int QDataType;
// 定义节点类型
typedef struct QueueNode {
struct QueueNode* next;
QDataType data;
} QueueNode;
// 定义队列类型
typedef struct Queue {
QueueNode* head;
QueueNode* tail;
} Queue;
// 队列的初始化
void QueueInit(Queue* pq);
// 队列的入队
void QueuePush(Queue* pq, QDataType x);
// 队列的出队
void QueuePop(Queue* pq);
// 返回队列的对头元素
QDataType QueueFront(Queue* pq);
// 返回队列的队尾元素
QDataType QueueBack(Queue* pq);
// 返回队列中的节点个数
int QueueSize(Queue* pq);
// 判断队列是否为空
bool QueueEmpty(Queue* pq);
// 销毁队列
void QueueDestroy(Queue* pq);
// 队列的初始化
void QueueInit(Queue* pq) {
assert(pq);
pq->head = NULL;
pq->tail = NULL;
}
// 队列的入队
void QueuePush(Queue* pq, QDataType x) {
assert(pq);
// 创建一个新节点
QueueNode* newNode = (QueueNode*)malloc(sizeof(QueueNode));
if (NULL == newNode) {
perror("malloc fail!\n");
exit(-1);
}
newNode->data = x;
if (NULL == pq->head) {
pq->head = newNode;
pq->tail = newNode;
pq->tail->next = NULL;
}
else {
pq->tail->next = newNode;
pq->tail = pq->tail->next;
pq->tail->next = NULL;
}
}
// 队列的出队
void QueuePop(Queue* pq) {
assert(pq);
assert(!QueueEmpty(pq));
QueueNode* next = pq->head->next;
free(pq->head);
pq->head = next;
// 如果对头为空了,我们也要把队尾也给置空,避免野指针
if (NULL == pq->head) {
pq->tail = NULL;
}
}
// 返回队列的对头元素
QDataType QueueFront(Queue* pq) {
assert(pq);
assert(!QueueEmpty(pq));
return pq->head->data;
}
// 返回队列的队尾元素
QDataType QueueBack(Queue* pq) {
assert(pq);
assert(!QueueEmpty(pq));
return pq->tail->data;
}
// 返回队列中的节点个数
int QueueSize(Queue* pq) {
assert(pq);
assert(!QueueEmpty(pq));
QueueNode* cur = pq->head;
int size = 0;
while (cur) {
size++;
cur = cur->next;
}
return size;
}
// 判断队列是否为空
bool QueueEmpty(Queue* pq) {
assert(pq);
return pq->head == NULL;
}
// 销毁队列
void QueueDestroy(Queue* pq) {
assert(pq);
assert(!QueueEmpty(pq));
QueueNode* cur = pq->head;
QueueNode* next = cur->next;
while (cur) {
next = cur->next;
free(cur);
cur = next;
}
pq->head = NULL;
pq->tail = NULL;
}
2.3、代码实现
有了以上思路和队列实现,那我们写起代码来也就水到渠成了:
int findTheWinner(int n, int k) {
int i = 0;
Queue queue;
QueueInit(&queue);
// 先将游戏成员全入队
for (i = 1; i <= n; i++) {
QueuePush(&queue, i);
}
while (QueueSize(&queue) > 1) {
for (i = 0; i < k - 1; i++) {
QueuePush(&queue, QueueFront(&queue));
QueuePop(&queue);
}
QueuePop(&queue);
}
int winner = QueueFront(&queue);
QueueDestroy(&queue);
return winner;
}
时间复杂度:O(nk),此方法和链表的基本一致。
空间复杂度:O(n),队列中最多有n个元素,故空间复杂度为O(n)。
大家可能都直到这一题其实就是我们可能听老师讲过的约瑟夫问题。
记得当初初次接触到这个约瑟夫问题的时候,模模糊糊的搞了一天也还是迷迷糊糊。如今再来看这个问题,就方法1的链表解法我大约用了10分钟不到就写出来了。
所以加大代码练习量是可以做到量变引起质变的!