🤔 原理

离散化，把无限空间中有限的个体映射到有限的空间中去，以此提高算法的时空效率。

通俗的说，离散化是在不改变数据相对大小的条件下，对数据进行相应的缩小。

有些数据本身很大，自身无法作为数组的下标保存对应的属性。
如果这时只是需要这堆数据的相对属性，那么可以对其进行离散化处理。
当数据只与它们之间的相对大小有关，而与具体是多少无关时，可以进行离散化。

😕 区间和

关说原理肯定是不行的，还是通过题目来加深理解。

原题链接

在这里插入图片描述

看到题目的第一眼可以确定的是，肯定是不能直接通过数组来进行操作，总不能直接开10^9 的数组吧，内存肯定是不够的。

可以发现每组数组中的有效数据是很稀疏的，那么我们就可以通过建立映射关系来创建一个新的数组，通过映射出来的数组进行区间和的操作。
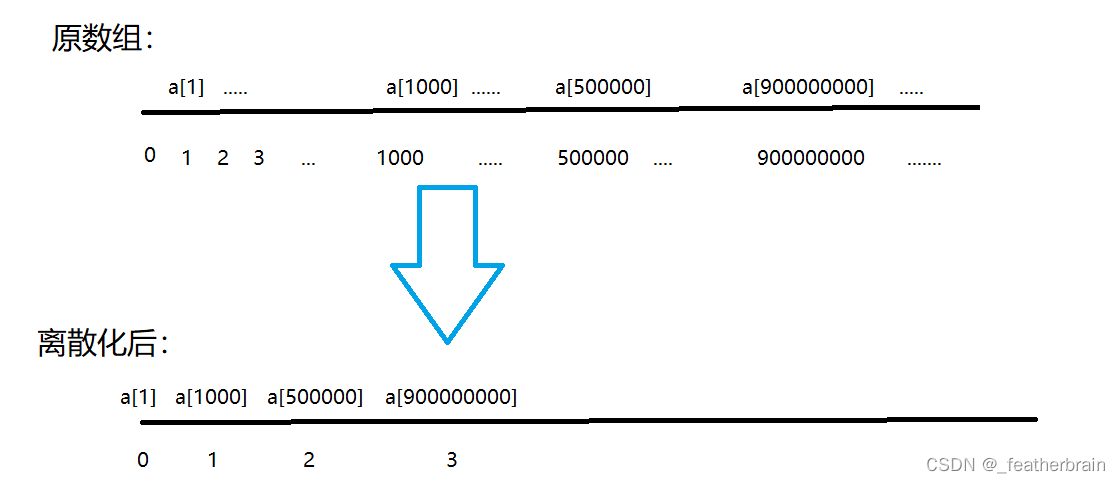
在这里插入图片描述
映射出来的数组的下标的相对位置跟原数组的下标的相对位置保持不变，那么通过下标来求区间和，也可以通过映射关系来进行求解。

😵‍💫 建立映射

映射关系的建立通过原数组中有效数据的下标来建立：

将数组中有效数据的下标放进数组中，排序加去重（排序是为了让相对位置保持不变，去重是为了提高效率），我们就可以通过这个下标数组中原数组有效数据的下标对应的下标来确定有效数据在新数组中的位置，从而构建出新数组。

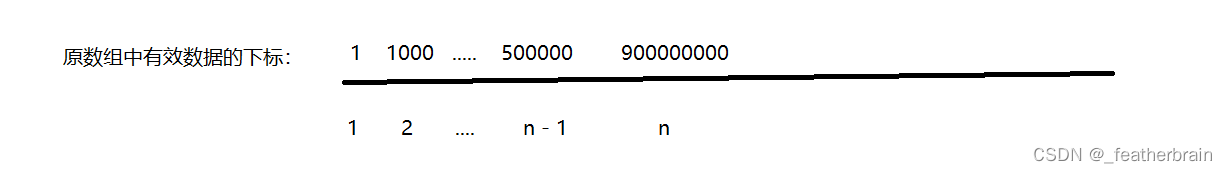
在这里插入图片描述

😵‍💫 查找映射的下标

寻找映射出来的下标时，下标数组是有序的，所以可以通过二分查找来进行查找。因为还涉及到前缀和的操作，所以我们需要将将返回的下标进行 +1 ，让下标从 1 开始，方便求前缀和数组。

😵‍💫 代码

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

const int N = 300010;
int a[N], s[N];     // a[]：映射后的数组，s[]：a[]的前缀和数组
int n, m;   // 插入次数和查询次数
vector<int> alls;   // 所有数据的下标
vector<pair<int, int>> adds, querys;    // adds：插入的下标和值，querys：查询的下标

// 查找映射的下标
int find(int x) 
{
    int l = 0, r = alls.size() - 1;
    while (l < r)
    {
        int mid = l + r >> 1;
        if (alls[mid] >= x) r = mid;
        else l = mid + 1;
    }
    
    return r + 1;
}



int main()
{
    cin >> n >> m;
    
    // 保存插入的下标和值
    for (int i = 0; i < n; i++)
    {
        int x, c;
        cin >> x >> c;
        adds.push_back({x, c});
        alls.push_back(x);
    }
    
    // 保存查询的下标和值
    for (int i = 0; i < m; i++)
    {
        int l, r;
        cin >> l >> r;
        querys.push_back({l, r});
        alls.push_back(l);
        alls.push_back(r);
    }
    
    // 排序 + 去重
    sort(alls.begin(), alls.end());
    alls.erase(unique(alls.begin(), alls.end()), alls.end());
    
    // 通过映射构建数组 ，add.first一定能找到
    for (auto& add : adds)
    {
        int i = find(add.first);
        a[i] += add.second;
    }
    
    // 构建前缀和数组
    for (int i = 1; i <= alls.size(); i++)
    {
        s[i] = s[i - 1] + a[i];
    }
    
    // 通过映射来查询区间和
    for (auto& query : querys)
    {
        int l = find(query.first);
        int r = find(query.second);
        cout << s[r] - s[l - 1] << endl;
    }
    
    
    return 0;
}