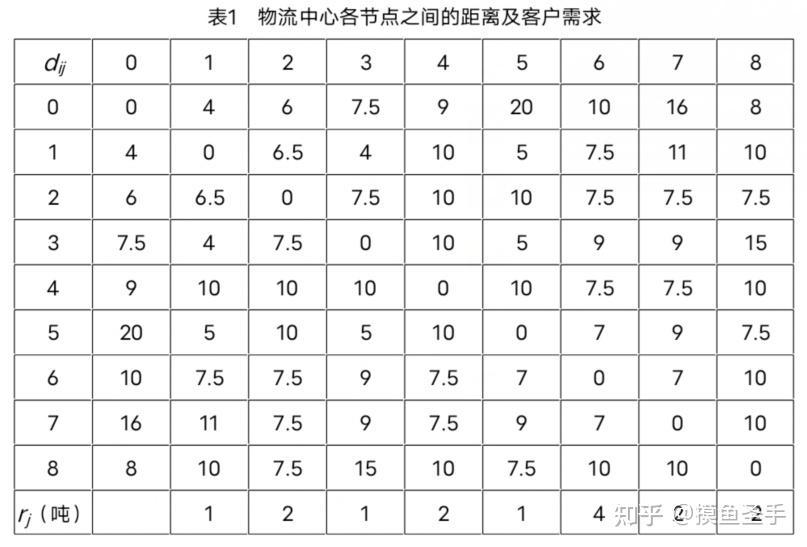
假定配送中心最多可以用2辆车对8个客户进行运输配送。每个车辆载重均 为8吨，车辆每次配送的最大行驶距离为50km，配送中心(编号0)与8个客 户之间及8个客户相互之间的距离d; (i, j= 1, 2, ... 8)、8个客户的货物需 求r;(j= 1, 2... 8)如表1所示。要求寻找一条路径， 使得配送总里程最 短。

这是一个典型的旅行商问题(TSP)，可以使用贪心算法或者动态规划进行求解。以下是一种基于贪心算法的解法：

1. 从配送中心出发，选择距离最近的客户进行配送，并将其需求量减去车辆载重;
2. 如果当前车辆还有剩余空间，则选择距离最近且需求量不超过剩余空间的客户继续配送;
3. 如果当前车辆已经无法再配送任何客户，则返回配送中心并换一辆新车继续上述步骤;
4. 当所有客户都得到了配送后，记录下当前的路径长度和路径;
5. 对所有可能的路径进行比较，选出最短的那条路径作为最终结果。

以下是C++实现代码：

#include <iostream>
#include <vector>
#include <algorithm>
#include <cstring>

using namespace std;

const int N = 10; //客户数目
const int M = 1 << N; //状态总数

int dist[N][N]; //存储两点之间的距离
int demand[N]; //存储每个客户的需求量
double f[M][N];