2022年长三角高校数学建模竞赛

C题隧道的升级改造与设计

原题再现：

某地现存一旧式双洞隧道，现计划将该隧道在旧貌基础上升级改造。在升级改造前，需进行定标与设计。考虑到该隧道洞壁附着特殊涂料，无人机在洞内通信信号较差，实地测量存在人身安全风险，建设指挥部已经通过某种技术手段得到该隧道从正上方俯拍的 CAD 航拍图（图 1，更清晰图像见附件 1）。现计划通过数学建模方法进行每个洞的中轴线的百米定标、安全评估与设计改造。
在这里插入图片描述
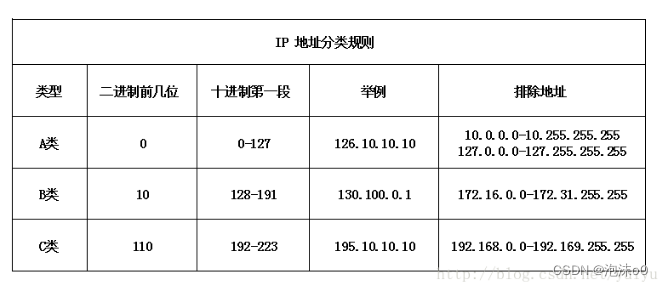
图1为隧道正上方俯拍图，即二维X-Z平面图。左洞起点坐标为A(91, 7, 349), 左洞终点坐标为 B(-617, 48, -1672)，单位为米（下同）；右洞起点坐标为 C(134, 7, 357)，右洞终点坐标为 D(-580, 48, -1685)。左洞行车方向为 AB，右洞行车方向为 DC。起点和终点均落在隧道单洞中轴线上。附件 2 是测得的隧道中轴线的 Z-Y高程数据。为安全起见，在修建过程中，该隧道的坡度一般不大于 3%；同时为利于排水，坡度一般不小于 0.3%。其中，坡度 a%指的是沿着 Z 方向每前进 1 米，Y 方向上升或下降 a%米。此外，为防止降雨天气对安全造成影响，隧道应尽量避免有积水区域。X、Y、Z 坐标轴方向参照图 1 中标示。请建立数学模型，解决以下问题：
1、建立隧道左右两洞的中轴线空间定标模型，计算左右两个隧道的长度，并给出左右两个隧道的百米定标。
2、根据隧道的空间定标和隧道建设安全要求，量化评价隧道的安全性。
3、隧道改造设计过程中，在尽可能满足隧道安全要求的前提下，还应考虑节省人力、物力资源的消耗。请从安全、经济等方面出发，研究如何对该隧道进行优化改造设计。改造后的结果请填入附件 3，并将其作为附件材料提交至参赛系统中。
相关说明
定标：即坐标的标定，其中空间定标是指准确标定出被描述物体的三维空间坐标。百米定标：沿行车方向标定隧道通行长度整百米处（如 100 米，200 米，300 米，……)的三维空间坐标。隧道长度：隧道的通行长度。

整体求解过程概述(摘要)

对于问题一，要建立隧道左右两洞的中轴线定标模型，以左侧隧道洞为例，首先我们根据附件 2 所给出的Y ~ Z 数据，利用非线性变换的傅里叶函数模型得到 y 与 z 之间的函数关系；另外从题目所给出的隧道正上方俯拍图，假设 x 与 z 满足分段函数的关系，从而确立隧道中轴线的空间模型。为了能够同时求出隧道总长度以及百米定标的三维坐标，我们采用了对 z 轴方向上进行线性插值，得到 10000 个 z 轴方向的数据，再根据 x,y,z之间的数量关系，得到相应的 x, y 的对应坐标。此时，隧道总长度就可以利用这 10000个插值得到的三维坐标通过两点间距离公式求出。而对于百米定标的这些三维坐标，只需要利用 matlab 软件编程，将 10000 个数据从初始值开始，当两点距离每相隔 100 米，就定一个百米坐标，依次类推，最后得到隧道的所有百米定标的具体数值坐标。
针对问题二，要求量化隧道的安全性，在问题一的基础上，我们直接利用附件 2 所给出的数据，根据题意坡度a%是指沿着 z 方向每前进 1 米，Y 方向上升或下降a%。求出两点间的坡度a% 的绝对值是否落在0.3% ~3% 这个范围内，并且为了安全防止隧道积水，隧道应避免起伏，呈单调型或开口下的抛物型。通过分析，最终得出结论：隧道无积水区域，但在坡度的建设要求上存在一定问题。
针对问题三，前面得的数据显示隧道安全性需要改进，即一部分点的坡度不在合理范围内。因此问题三可以看作是一个有约束条件的最优化问题。目标函数是最小化隧道长度，约束条件为（1）隧道单调上升或单调下降，建立不等式约束；（2）隧道坡度绝对值应在0.3% ~ 3% 之间，建立不等式约束；（3）起止点坐标，建立等式约束。通过求解带线性约束的二次优化问题，得到了对应 Y 的最优值，既保证了坡度在合理范围内，又使得隧道长度最小，达到节省材料的目的。
本文主要运用 MATLAB 软件对相关数学模型进行编程求解，计算快捷、准确，整篇文章采取图文并茂的方式去呈现。文章最后对模型做了评价与推广，结果正确合理，具有一定的价值。

模型假设：

1、假设在俯视平面ZOX 上，左洞隧道在原点处两侧为直线；
2、假设在俯视平面ZOX 上，右洞隧道与左洞隧道平行；
3、假设记录的数据除缺失外准确无误；
4、假设隧道所在的山体密度均等；

问题分析：

对于问题一的分析
为得到隧道总长度及百米定标坐标，我们需要建立隧道左右两洞的中轴线定标模型。以左洞为例，首先根据附件 2 所给出的Y、Z 坐标数据，利用 matlab 软件拟合工具箱中的非线性变换傅里叶函数得到坐标 y 与坐标 z 之间的函数关系 y = f (z)。
另外，观察附件 1 中的隧道图，发现隧道存在弯折现象，现假设 x 与 z 之间满足分段函数 x = g(z) 的关系式，且两段函数均为直线方程，弯折的地方设为分段函数原点。这样我们就能够获得左洞中轴线空间位置模型。右洞同理。
对于隧道长度及百米定标，我们利用类极限的方式，将出入口的坐标在 z 轴方向上进行 10000 等分，根据 y = f (z) 及 x = g(z) 关系式求得对应的 x 值及 y 值，从而得到这10000 个点的坐标。对相邻坐标之间的距离求和得到近似于隧道的总长度。同时我们也可得出隧道每百米的位置坐标。
对于问题二的分析
为量化隧道安全性，首先考虑隧道坡度，再考虑隧道是否会积水，根据附件 2 的数据，可以很容易的求出相邻两点之间的坡度，对比隧道安全指标（即范围在 0.3%~3%之间），筛选出异常的坐标点。
另外为验证隧道是否会积水，画出Y 与Z 的关系图，分析隧道高度是否存在起伏或先下后上的情况。结果发现左洞隧道和右洞隧道从起点到终点高度都是先上升后下降不会积水。
对于问题三的分析
对隧道的优化有两方面，一是安全性问题，即隧道坡度满足要求且无积水。二是经济问题，即隧道总长度应该最小。在确保安全性的同时我们需要减少工程量，确保用最少的改动解决问题。
本问题为一个带线性约束的二次优化问题，根据附件 3 中的 z 坐标值计算出优化后的 y 坐标。利用 matlab 的优化函数可以方便的解决此类问题。

模型的建立与求解整体论文缩略图

在这里插入图片描述

全部论文请见下方“ 只会建模 QQ名片” 点击QQ名片即可

部分程序代码：(代码和文档not free)

filename = './附件 2.xlsx';
leftsheet = '左洞高程';
rightsheet = '右洞高程';
leftxlRange = 'A2:B99';
rightxlRange = 'A2:B98';
left = xlsread(filename,leftsheet,leftxlRange);
right = xlsread(filename,rightsheet,rightxlRange);
% 问题一（左洞） 先处理左洞的
% 起止位置分别是：（91， 349）；（-617，-1672）
leftZ = left(:, 1); % 98 行
leftZ = [349; leftZ; -1672];
plot(linspace(-617, 91, 100), -flipud(leftZ))
% 建立方程，先建立左洞的。假设左洞与右洞平行，则将左洞平移即可得到右洞方程
% 左洞方程为分段函数
A = [91, 7, 349];
B = [-617, 48, -1672];
C = [134, 7, 357];
D = [-580, 48, -1685];
F_leftZlillte0 = @(x)x * B(3) - B(1);
F_leftZgrater0 = @(x)x * A(3) - A(1);
X_leftlinear = -20;
X_leftlog = 100;
% options = optimoptions('fsolve','Display','iter');
coeff_leftlillte0 = fsolve(F_leftZlillte0, X_leftlinear); % coeff_leftlinear = 0.369
coeff_leftgreater0 = fsolve(F_leftZgrater0, X_leftlog); % coeff_leftlog = 0.26
% coeff_leftlog = 92 / log(349);
left_all = [left, ones(98, 1)];
left_all = [flip(A); left_all; flip(B)]; % 100 个
for i = 1:size(left_all, 1)
Z = left_all(i, 1);
if Z <= 0
left_all(i, 3) = coeff_leftlillte0 * Z;
else
left_all(i, 3) = coeff_leftgreater0 * Z;
end
end
left_all;

Z_true = left_all(:, 1);
Y_true = left_all(:, 2);
a0 = 33.43 ;
a1 = -18.3 ;
b1 = -9.837 ;
a2 = 2.14 ;
b2 = -3.245 ;
a3 = 2.985 ;
b3 = -0.8842 ;
w = 0.002124 ;
Z_hat = flip(linspace(B(3), A(3), 10000))';
X_hat = ones(size(Z_hat, 1), 1);
Y_hat = ones(size(Z_hat, 1), 1);
for i = 1: size(Z_hat, 1)
if Z_hat(i) >= 0
X_hat(i) = coeff_leftgreater0 * Z_hat(i);
else
X_hat(i) = coeff_leftlillte0 * Z_hat(i);
end
Y_hat(i) = a0 + a1*cos(Z_hat(i)*w) + b1*sin(Z_hat(i)*w) + a2*cos(2*Z_hat(i)*w) +
b2*sin(2*Z_hat(i)*w) + a3*cos(3*Z_hat(i)*w) + b3*sin(3*Z_hat(i)*w);
end

meter = [Z_hat, Y_hat, X_hat];
meter(:, 4) = 0;
meter(:, 5) = 0;
for i = 1: size(meter, 1)
if i > 1
meter(i, 4) = sqrt((meter(i, 1) - meter(i-1, 1))^ 2 + (meter(i, 2) - meter(i-1,
2))^ 2 + (meter(i, 3) - meter(i-1, 3))^ 2);
meter(i, 5) = sum(meter(1:i, 4));
end
end
meter_100_num = floor(max(meter(:, 5)) / 100);
meter_100_location = zeros(meter_100_num, 4);
for i = 1: meter_100_num
[~, I] = min(abs(meter(:, 5) - i * 100));
meter_100_loaction(i, 1) = meter(I, 1);
meter_100_loaction(i, 2) = meter(I, 2);
meter_100_loaction(i, 3) = meter(I, 3);
meter_100_loaction(i, 4) = meter(I, 5);
end
隧道总长度
max(meter(:, 5))