一、单纯形法的求解思路
单纯形法求解线性规划的思路:在高斯消去法的基础上,发展为求解变量数大于方程数,并且使目标函数值优化的方法。从线性方程中找到一个个的单纯形,每个单纯形(图形的顶点)可以得到一组解,然后再判断该目标函数值是增大还是变小,决定下一步选择的单纯形,这就是迭代,直到目标函数实现最大值或者最小值为止。
简单的说就是:从可行域的一个顶点到另一个顶点迭代求最优解。
二、单纯形法的求解过程
1、计算原理:
初始基可行解的确定
最优性检验与解的判别
基变换——从非基变量中找一个变量交换原基变量
迭代(旋转运算)——换入变量转换为基变量
2、计算步骤
使用单纯形表来计算——另一种形式的增广矩阵
(1)根据数学模型确定初始可行解,建立初始单纯形表。
(2)计算各非基变量 的检验数是
的检验数是
 若
若
则已得到最优解,可终止计算。否则转入下一步。
(3)在 >0,j = m+1,...,n中,若有某个
>0,j = m+1,...,n中,若有某个 对应
对应 的系数列向量
的系数列向量 ,则此问题属无界,终止计算。否则,转入下一步。
,则此问题属无界,终止计算。否则,转入下一步。
(4)根据max( >0)=
>0)= ,确定
,确定 为换入变量。按
为换入变量。按 规则计算
规则计算

可确定 为换出变量,转入下一步。
为换出变量,转入下一步。
(5)以 为主元素进行迭代(即用高斯消去法或称为旋转运算),把
为主元素进行迭代(即用高斯消去法或称为旋转运算),把 所对应的列向量
所对应的列向量
 变换为
变换为
将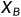 列中的
列中的 换为
换为 ,得到新的单纯形表。重复(2)~(5),直达终止。
,得到新的单纯形表。重复(2)~(5),直达终止。
三、单纯形表计算举例
1、标准化,建立单纯形表
引入松弛变量x3,x4,x5为初始基变量
max z = x1 + 3x2 + 0x3 + 0x4 + 0x5
x1 + 2x2 + x3 = 8
4x1 + x4 = 16
4x2 + x5 = 12
x1,x2,x3,x4,x5 ≥ 0
2、建立单纯形表

3、重复循环基变换