预测包括，数值拟合，线性回归，多元回归，时间序列，神经网络等等

对于单变量的时间序列预测：模型有AR,MA,ARMA,ARIMA，综合来说用ARIMA即可表示全部。

数据和代码链接：数据和Jupyter文件

以预测美国未来10年GDP的变换情况为列：

目录

第一步进行数据导入

第二步进行平稳序列分析

​第三步进行不平稳序列的差分运算

第四步进行模型定阶和模型选择及拟合

​第五步进行模型结果分析和模型检验 

第六步进行模型预测

PS：自动化AUTO-ARIMA的比较

---

ARIMA流程图如下：

第一步进行数据导入：

    观察要预测变量的数据情况，去除杂数据，得到数据本身的属性如：大小，类型等

import pandas as pd,numpy as np
from matplotlib import pyplot as plt

#加载数据，sheet_name指定excel表的数据页面，header指定指标column属性，loc去除杂数据，可选：parse_dates=['']，index_col='',use_cols=['']
df=pd.read_excel('./data/time1.xls',sheet_name='数据',header=1).loc[1:,:]

#DateFrame索引重置
df=df.set_index('DATE')#df.set_index('DATE',inplace=True)

#查看前5行
print(df.head(5))

#查看列索引
print(df.columns)#print(df.keys())

#查看表的维度
print(df.shape)

#查看行索引
print(df.index)

#np.array()  array1.reshape(,)  df.values.astype(int).tolist() np.vstack((a1,a2))  np.hstack((a1,a2))  round()  iloc

#时间索引拆分
# dates=pd.date_range(start='1991-01-01',end='2007-08-01',freq='MS')#日期取值和格式转换，MS代表每月第一天
# years=[d.strftime('%Y-%m') for d in dates][0:200:25]
# years.append('2007-09')

结果如下：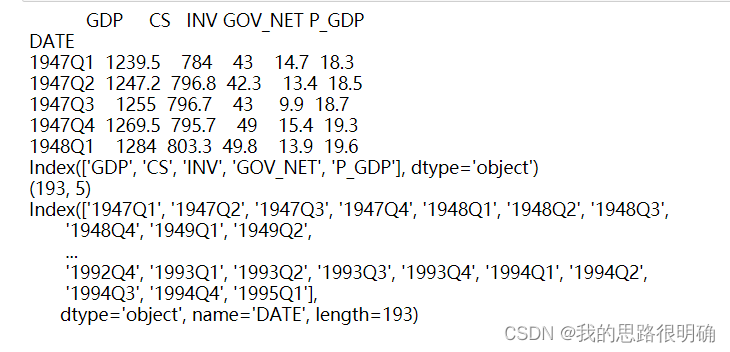

第二步进行平稳序列分析：

    我们研究分析的时间序列，即面板数据，只有是宽平稳的才有研究意义，如果是非平稳序列需要将其差分转换为平稳序列才能进行分析，
    对于严平稳序列，性质不变化，即序列为白噪声序列，这样的序列没有研究意义。
    
    所以这里拿到GDP的时间序列数据后，先进行原序列的白噪声检验，利用LB统计量，若p值小于显著水平a=0.05，即认为原序列为非白噪声
    序列，有研究的意义。
    
    接着画时序图，主观上判断GDP时间序列的平稳情况，若呈现明显的趋势性，则为非平稳序列；若没有明显趋势，或者出现你不好判断平
    稳的情况，这时候你需要借助ADF单位根统计量来进行辅助判断它是否平稳。对于ADF统计量，你可以比较统计量的值来判断，也可以比较
    p值来判断，如显著水平a=0.05时候，如果你变量的ADF统计量小于a=0.05对于的ADF统计量，则说明该变量对应的时间序列为平稳序列；
    还一种更为直接的方法是，只需要判断该变量的p值如果小于0.05，则也说明为平稳序列。
   

plt.rcParams['axes.unicode_minus'] = False  # 解决保存图像是负号'-'显示为方块的问题
plt.rc('font',family='SimHei')
plt.style.use('ggplot')

df.plot(secondary_y=['CS','INV','P_GDP','GOV_NET'])#单个指标时序图 df['CS'].plot()
plt.xlabel('Date')
plt.ylabel('Value')
plt.title('Time Series Plot')
#plt.grid()
plt.show()

from statsmodels.tsa.stattools import adfuller# ADF检验

for i in df.columns:
    data=df[i]
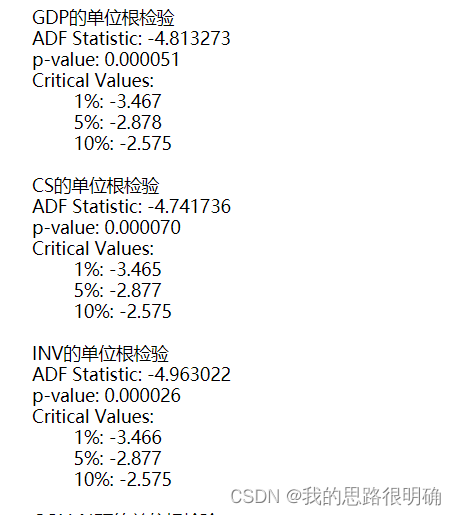
    print(f'{i}的单位根检验')
    result = adfuller(data)#默认情况下，regression参数为'c'，表示使用包含截距项的回归模型。
    print('ADF Statistic: %f' % result[0])#ADF统计量
    print('p-value: %f' % result[1])#p值
    print('Critical Values:')#在置信水平下的临界值
    for key, value in result[4].items():
        print('\t%s: %.3f' % (key, value))
    print()

代码结果：

第三步进行不平稳序列的差分运算：

    一般时间序列的差分不会超过三阶，对原始数据进行差分运算，重复第二步的时序图和ADF单位根检验操作，若发现差分后的序列为平稳
    序列，则记下差分的阶数，这里GDP的差分阶数1，通过了平稳序列检验。再次对差分后的序列进行白噪声检验，若通过为非白噪声序列，
    则进行下一步操作。
    

#差分时序图
diff_data = df.diff(periods=1).dropna()# 创建一阶差分的时间序列，加上dropna()后续不需要执行[1:]
#print(diff_data)

diff_data.plot()
plt.xlabel('Date')
plt.ylabel('Value')
plt.title('Time Series Plot')
#plt.grid()
plt.show()

for i in diff_data.columns:
    data=diff_data[i]#Series索引选取，一阶差分第一个数据为NA
    
    print(f'{i}的单位根检验')
    result = adfuller(data)#结果对应位置的数据需要自己判断是什么含义
    print('ADF Statistic: %f' % result[0])#ADF统计量
    print('p-value: %f' % result[1])#p值
    print('Critical Values:')#在置信水平下的临界值
    for key, value in result[4].items():
        print('\t%s: %.3f' % (key, value))
    print()

from statsmodels.stats.diagnostic import acorr_ljungbox

#这里为一阶差分后的平稳序列进行白噪声检验，lags为1，否则lags为0，这里拿上述的GDP指标进行
lags = [1,4,8,16,32]

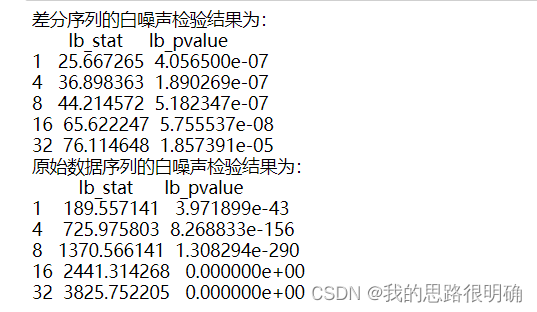
print('差分序列的白噪声检验结果为：'+'\n',acorr_ljungbox(diff_data['GDP'], lags))  # 返回统计量和p值,这里的lags对应差分阶数

print('原始数据序列的白噪声检验结果为：'+'\n',acorr_ljungbox(df['GDP'], lags))

代码结果如下：

第四步进行模型定阶和模型选择及拟合：

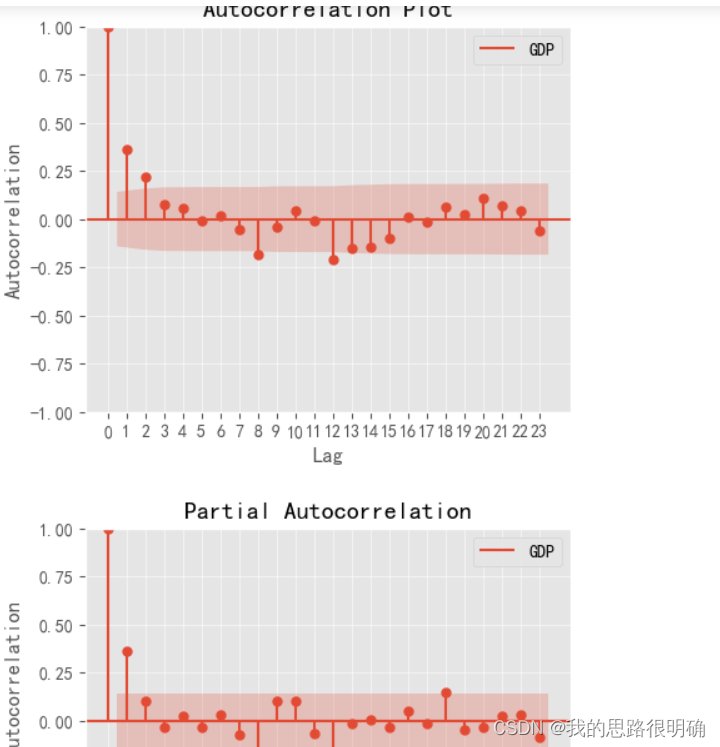
    模型定阶先采用自相关图和偏自相关图进行初步判断：
           自相关系数                偏自相关系数             差分
    AR             拖尾                          p阶截尾                      0
    MA            q阶截尾                    拖尾                            0
    ARMA       拖尾                          拖尾                            0
    ARIMA      拖尾                          拖尾                            d
    总之，上述的模型都可以用ARIMA(p,d,q)来实现，AR,MA,ARMA都是ARIMA的特殊情况。
    
    对于拖尾和截尾的经验判断：
    拖尾：负指数单调收敛到0，或者呈现余弦式衰减
    截尾：迅速衰减到0，并且在0附近波动
    截尾比拖尾趋近于0更加迅速，截尾在后期不会再有明显的增加
    
    在利用图表进行初步判断后，依旧无法拿准模型的阶数，可以利用AIC和BIC准则进行辅助判断，或者叫做优化。比如我判断模型的阶数可能为
    2，1，4，或者3，1，3，这时候我拿不准，你可以先做ARIMA(2,1,4)，如果发现后续的模型显著性检验和参数检验都通过了，那么你可以直接
    利用ARIMA(2,1,4)进行预测并得到结论，但你或许也去尝试附近的几个阶数，发现ARIMA(3,1,3),ARIMA(2,1,3)等等也通过了，但是ARIMA
    (3,1,3)的AIC和BIC的值是最小的，即该模型的拟合精度更高，是一个相对最优的模型，这一步便是模型的优化。
    
    这边的定阶和优化在python里的实现是：从q为0到（数据长度/10），从p为0到（数据长度/10），一般阶数不会超过（数据长度/10）；
    然后进行q*p次模型拟合，利用模型拟合的结果比较AIC和BIC的值，BIC值越小越小的那个模型就是相对最优模型，再用该模型的阶数作为
    最终模型拟合的阶数。
    

#生成自相关图，偏自相关图
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf

fig, ax = plt.subplots(figsize=(5, 4))
plot_acf(diff_data['GDP'],ax=ax)#可以换成df的数据，这里用一阶差分数据得到平稳序列
    
ax.set_title("Autocorrelation Plot")
lags=list(range(24))
ax.set_xticks(lags)#这里把x坐标刻度变更精细，加网格图更方便,xticklabels替换标签
ax.set_xlabel("Lag")
ax.set_ylabel("Autocorrelation")
ax.grid(alpha=0.5)
plt.legend(['GDP'])#这里区别直接放入df.columns[i]，如果是多字符如‘CS’，这样会被认为是一个序列，拆成C和S的图例
plt.show()
    
fig, ax = plt.subplots(figsize=(5, 4))
lags=list(range(24))
ax.set_xticks(lags)#这里把x坐标刻度变更精细，加网格图更方便,xticklabels替换标签
plot_pacf(diff_data['GDP'], ax=ax,method='ywm')#ywm替换默认的yw，去除警告
ax.set_xlabel('Lags')
ax.set_ylabel('Partial Autocorrelation')
ax.grid(alpha=0.5)
plt.legend(['GDP'])
plt.show()

import warnings
warnings.filterwarnings("ignore")
import statsmodels.api as sm


#diff_data['GDP'].values.astype(float),这里发现Serise的dtype为object，模型用的应该为float或者int类型，需要注意原数据的数据类型是否一致

Min=float('inf')
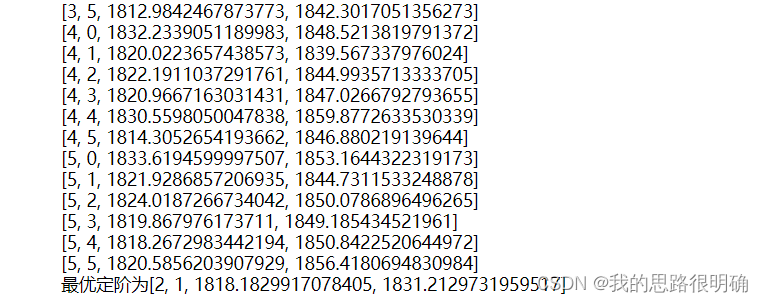
for i in range(0,6):#AIC，BIC最小找到p，q阶数来定阶，从0开始定阶是否可行？？
    for j in range(0,6):
        result=sm.tsa.ARIMA(df['GDP'].values.astype(float),order=(i,1,j)).fit()
        print([i,j,result.aic,result.bic])
        if result.bic<Min:
            Min=result.bic
            best_pq=[i,j,result.aic,result.bic]
print(f'最优定阶为{best_pq}')

代码结果：

第五步进行模型结果分析和模型检验 

    模型检验分为模型参数检验和模型显著性检验。

    模型显著性检验：即残差的白噪声检验，若残差为白噪声序列，即原序列信息提取充分，看LB统计量，python中模型结果的LB统计量
    即为残差的LB统计量，若p值小于0.05，则为非白噪声序列，若p值大于0.05，则说明残差为白噪声序列，这是我们想要的结果。
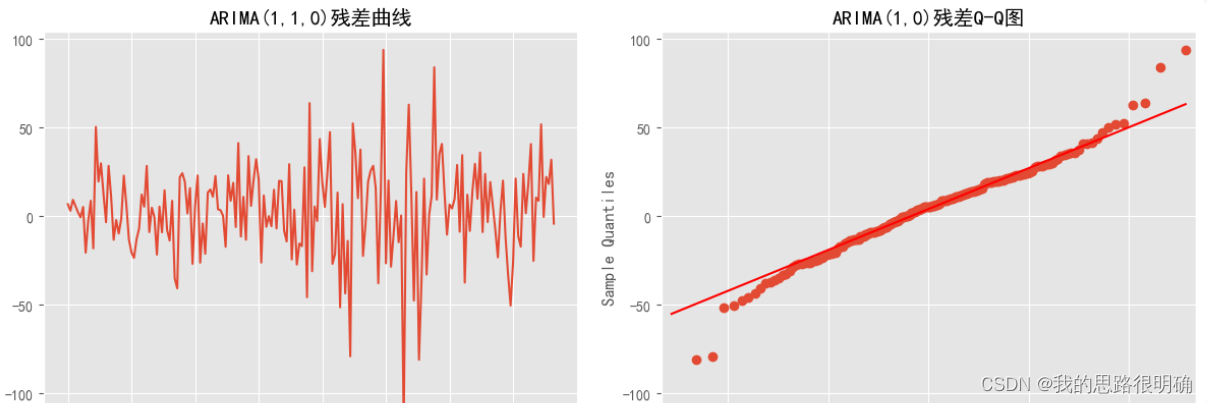
    这里你可以单独拿出模型的残差值，自己绘制残差的时序图，QQ图，正态分布图，或者自己进行白噪声检验辅助判断。白噪声序列即
    服从正态分布，时序图是平稳波动,QQ图上的数值点在对角线附近。
    
    模型的参数检验：检验每一个未知参数是否显著为0，检验模型是否最精简。参数不显著非零，则可以从拟合模型从剔除，看t统计量。
    
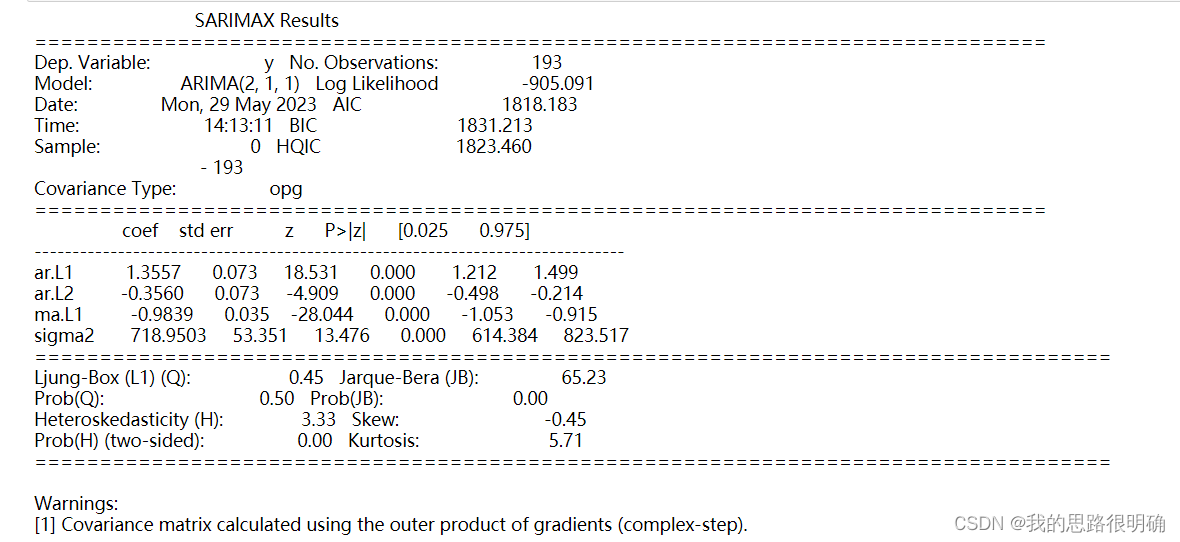
    模型结果部分解释：
    const：常数项       
    ar.L1：自回归项系数
    ma.L1：移动平均项系数
    sigma2：方差
    各个参数下的P>|z|这一行，若小于a=0.05则拒绝原假设，认为参数显著非0，即不需要简化模型。
    Ljung-Box：LB统计量,这里需要注意的是LB的P值需要>0.95,即判断残差序列为白噪声序列，小于0.05为非白噪声序列。
    Jarque-Bera：JB统计量   
    Heteroskedasticity检验的结果表明方差稳定情况

Result=sm.tsa.ARIMA(df['GDP'].values.astype(float),order=(best_pq[0],1,best_pq[1])).fit()
print(Result.summary())  #显示模型的所有信息

print(len(Result.resid))
#print(Result.resid)这里观察到残差的第一项为原数据的1239.5，即差分数据不管第一项，这里需要调整残差的观测

#这里就可以观察到原始模型的结果LB统计量和这里的白噪声检验是一致的，p>0.05,即认为残差为白噪声序列，原序列信息提取充分。
lags = [1,4,8,16,32]
print('差分序列的白噪声检验结果为：'+'\n',acorr_ljungbox(Result.resid[1:], lags))

## 查看模型的拟合残差分布
fig = plt.figure(figsize=(12,5))
ax = fig.add_subplot(1,2,1)
plt.plot(Result.resid[1:])
plt.title("ARIMA(2,1,1)残差曲线")

## 检查残差是否符合正太分布
ax = fig.add_subplot(1,2,2)
sm.qqplot(Result.resid[1:], line='q', ax=ax)
plt.title("ARIMA(2,1,0)残差Q-Q图")
plt.tight_layout()
plt.show()

fig = plt.figure(figsize=(12,5))
Residual=pd.DataFrame(Result.resid[1:])
Residual.plot(kind='kde', title='密度')
plt.legend('')
plt.show()

代码结果为：

  

第六步进行模型预测：

    模型预测即利用上述的相对最优模型进行原始数据变量后续时间对应的值的预测。
    注意在python中，predict函数如果是对差分数据进行预测，注意start的起始和end的中止情况，比如一阶差分的数据是从第二个观测值
    开始进行，对应的残差也是如此，在后续绘图的时候需要注意到差分模型绘图的情况。

#预测，绘制原序列和预测序列值对比图

Predict=Result.predict(start=1, end=len(df['GDP'])-1+1+10); #不加参数默认0到n-1，要加预测个数在end后面N-1+预测n即可
#如果是一阶差分的序列预测，第一个数据已经差分消去了，应该start从第二个观测数据开始，即n=1；如果是0阶，则不需要按默认0到n-1

print(list(zip(range(193,203),Predict[-10:])))#打印预测值

plt.figure()
plt.plot(range(193),df['GDP'].values)#'o-k'
plt.plot(range(193+10),Predict)#'P--'
plt.legend(('原始观测值','预测值'))
plt.xticks(list(range(0,203,10)),rotation=90)
plt.show()

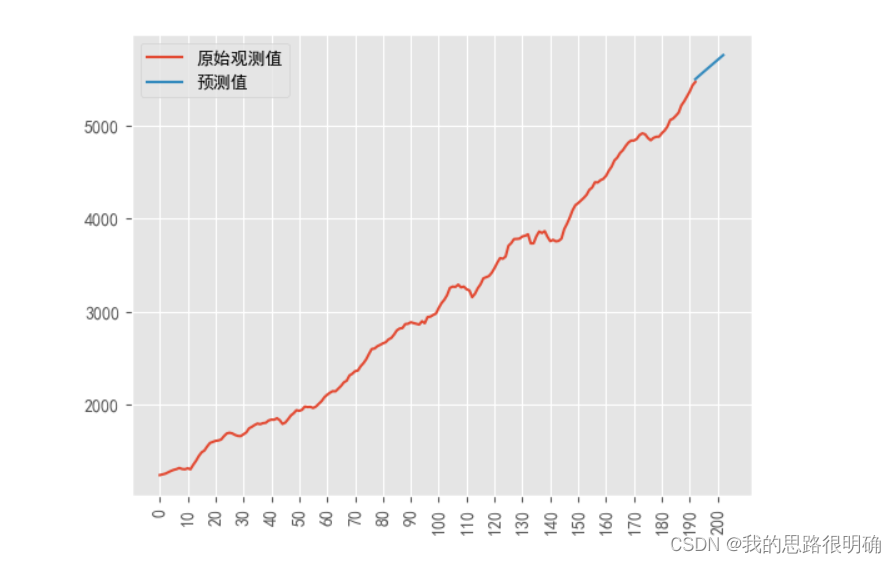
plt.figure()
plt.plot(range(193),df['GDP'].values)#'o-k'
plt.plot(range(192,193+10),Predict[-11:])#'P--'#接着原数据最后一个，进行拟合预测表示
plt.legend(('原始观测值','预测值'))
plt.xticks(list(range(0,203,10)),rotation=90)
plt.show()

代码结果：

PS：自动化AUTO-ARIMA的比较

import pmdarima as pm
# ## 自动搜索合适的参数
model = pm.auto_arima(df['GDP'].values,
                      start_p=1, start_q=1, # p,q的开始值
                      max_p=12, max_q=12, # 最大的p和q
                      d = 0,            # 寻找ARMA模型参数
                      m=1,              # 序列的周期
                      seasonal=False,   # 没有季节性趋势
                      trace=True,error_action='ignore',  
                      suppress_warnings=True, stepwise=True)
 
print(model.summary())

这一块个人没有深入研究，auto的方法有优点也有缺点， 也算提供一个写代码的思路。