东莞理工学院的同学可以借鉴，请勿抄袭

1.实验目的

通过实验达到：

理解和掌握图的基本概念、基本逻辑结构；
理解和掌握图的邻接矩阵存储结构、邻接链表存储结构；
理解和掌握图的 DFS、BFS 遍历操作的思想及其实现；
加深对堆栈、队列的概念及其典型操作思想的理解；
理解和掌握图的应用-最小生成树、最短路径算法的思想及其实现；
掌握典型图操作算法的算法分析。

2. 实验题目：图的建立、遍历及其应用

设图结点的元素类型为 ElemType(可以为 char 或 int)，通过文件读取方式，建立一个不少于10个顶点的带权无向图G，实现以下图的各种基本操作的程序：

① 用邻接矩阵作为储结构存储图 G 并输出该邻接矩阵；

② 用邻接链表作为储结构存储图 G 并输出该邻接链表；

③ 按深度优先遍历(DFS)算法输出图 G 中顶点的遍历序列；

④ 按广度优先遍历(BFS)算法输出图 G 中顶点的遍历序列；

⑤ 使用 Prime 算法(或者 Kruskal 算法)从某个指定的顶点出发输出图 G 的最小生成树；（要求把最小生成树的各条边输出成 A-B-wight,或者 (A,B,weight)的形式）；

⑥ 求从有向图的某个节点出发到其余各顶点的最短路径和最短路径值；（带权有向图）；

⑦ 主函数通过菜单选择函数调用实现以上各项操作，请在实验报告中请画出设计的图。

附加题：（每完成一个额外附加 5 分，上限 10 分）

① 编写函数求邻接矩阵存储结构的有向图 G 中各顶点的入度和出度；

② 用狄克斯特拉（Dijkastra）算法或者 Floyd 算法求每对顶点之间的最短路径；（带权有向图）。

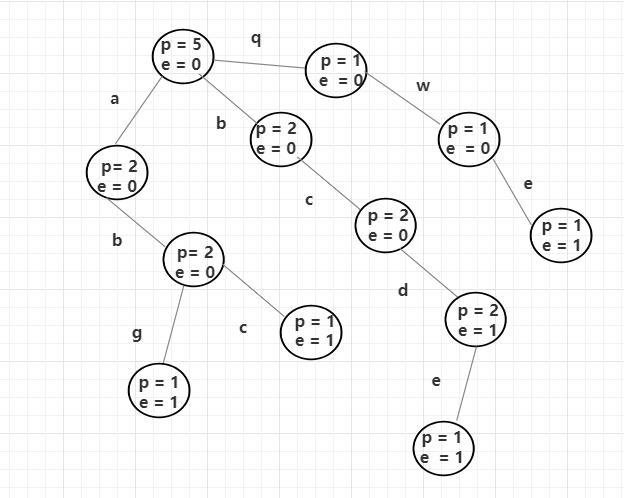
一个无向图的例子,可以把此图扩展作为实验用图：

在这里插入图片描述

2.1. 数据结构设计

typedef char ElemType;

typedef struct GraphByMatrix {
	//顶点数组
	ElemType* arrayV;

	//邻接矩阵
	int** matrix;

	//有向or无向
	int isDirect;

	int size;

}GraphByMatrix;

typedef struct Node {
	int src;
	int dest;
	int weight;
	struct Node* next;
}Node;

typedef struct GraphByList {
	Node** edges;
	ElemType* arrayV;
	int isDirect;
	int size;//顶点个数
}GraphByList;

2.2. 主要操作算法设计与分析

2.2.1. 读文件建立邻接矩阵并输出

GraphByMatrix* createMByFile(char* file);

GraphByMatrix* createGByM(ElemType* arrayV, int n, int flag);

int getIndexM(GraphByMatrix* pg, ElemType v);

void addEdgeM(GraphByMatrix* pg, ElemType v1, ElemType v2, int weight)

void printMatrix(GraphByMatrix* pg)

返回类型：GraphByMatrix*；

是否有参数：char* file，（文件名）

步骤：

根据固定的文件格式读取对应信息
第一个整数为顶点的个数，空格分割后是一个字符串，是顶点，然后一个回车，每行一条边，边的格式为起始顶点 + 空格 + 目的顶点 + 空格 + 权重
定义getIndexM函数，获取顶点在邻接矩阵中的下标
定义createGByM函数通过文件构造不包含权重的邻接矩阵初始化版本
定义addEdgeM函数给邻接矩阵增加边，循环读取文件直到结束
读取文件结束后，返回邻接矩阵
通过printMatrix函数打印邻接矩阵

算法时间复杂度：

时间复杂度为O(N);
空间复杂度为O(N²);

2.2.2 读文件建立邻接链表并输出

Node* newNode(int src, int dest, int weight);

GraphByList* createGByL(ElemType* arrayV, int n, int flag);

GraphByList* createLByFile(char* file);

int getIndexL(GraphByList* pg, ElemType v);

void addEdgeL(GraphByList* pg, ElemType src, ElemType dest, int weight);

void printList(GraphByList* pg);

返回类型：GraphByList*；

是否有参数：char* file，（文件名）

步骤：

根据固定的文件格式读取对应信息
第一个整数为顶点的个数，空格分割后是一个字符串，是顶点，然后一个回车，每行一条边，边的格式为起始顶点 + 空格 + 目的顶点 + 空格 + 权重
定义getIndexL函数，获取顶点在邻接表中的下标
定义createGByL函数通过文件构造不包含权重的邻接表初始化版本，即数组的值都为null，暂无链表的情况
定义addEdgeL函数，为邻接表增加边，在顶点对应下标的数组的链表上头插一个节点，这个节点由newNode函数构造
文件读完后返回邻接表
通过printList函数打印邻接表

算法时间复杂度：

时间复杂度为O(N);
空间复杂度为O(N);

2.2.3. 按深度优先遍历(DFS)算法输出图 G 中顶点的遍历序列

void dfs(GraphByMatrix* pg, ElemType v);

void dfsOrder(GraphByMatrix* pg, int src, int* isVisited);

返回类型：无返回值；

是否有参数：有，GraphByMatrix*邻接矩阵，char 起始顶点

步骤：

定义一个数组标记顶点是否被打印过，调用getIndexM函数获取顶点对应的下标
调用递归函数dfsOrder，传入邻接矩阵，下标，标记数组
打印过的则不能再打印，由于是连通图，所以任何一个顶点都能够打印所有顶点
一直递归至结束，回到dfs函数，释放临时的空间

算法时间复杂度：

时间复杂度为O(N);
空间复杂度为O(N);

2.2.4. 按广度优先遍历(BFS)算法输出图 G 中顶点的遍历序列

导入一个队列结构体Queue与其基本方法；（见附件）

void bfs(GraphByMatrix* pg, ElemType v);

返回类型：无返回值；

是否有参数：有，GraphByMatrix*邻接矩阵，char 起始顶点

步骤：

定义一个队列对象
定义一个数组标记顶点是否被打印过，调用getIndexM函数获取顶点对应的下标
让下标入队列
进入循环，出队列一个元素并打印，标记数组标记其打印过，循环此顶点所连顶点入队列，并标记数组为打印过（两层保证，防止打印多次）
直到队列为空，循环结束，释放临时的空间

算法时间复杂度：

时间复杂度为O(N);
空间复杂度为O(N);

2.2.5. 使用 Prime 算法输出图 G 的最小生成树

导入一个优先级队列结构体PriorityQueue与其基本方法；（见附件）

定义一个Edge类，代表边

typedef struct Edge {
	int src;
	int dest;
	int weight;
}Edge;
Edge newEdge(int src, int dest, int weight) {
	Edge e = { src, dest, weight };
	return e;
}

void prime(GraphByMatrix* pg, ElemType v);

无返回值，有参数，邻接矩阵和起始顶点

步骤：

获取顶点下标
申请两部分空间，一部分代表起始顶点集合，一部分代表目的顶点集合，并进行初始化
定义一个优先级队列，并将v对应的所有边都入堆
进入循环，取出堆顶元素，如果这条边的起始顶点不存在于起始顶点集合，则可以打印这条边，打印后将此起始顶点加入起始顶点集合，目的顶点集合删除这个顶点，将此目的顶点的所有边都入堆
直到堆为空或者打印的边数为n-1，退出循环，释放临时的资源

复杂度分析：

时间复杂度：O(N²)

空间复杂度：O(N)

2.2.6. SPFA最短路径

导入队列结构体Queue及其基本方法；（见附件）

void SPFA(GraphByMatrix* pg, ElemType src, int* dist, int* path)

void printPath(GraphByMatrix* pg, int* dist, int* path, int srcIndex)

void printMinPath(GraphByMatrix* pg, ElemType v);

无返回值，传入邻接矩阵，起始顶点，dist最短路径长数组，path路径数组

步骤：

在printMinPath中，定义dist和path数组
调用SPFA函数，传入dist和path
在SPFA函数中，对dist和path进行初始化
定义一个队列
将起始顶点入队列
进入循环，每次取出队头元素，进行松弛操作，松弛成功，将其目的顶点入队列
直到队列为空
调用printPath打印最短路径

复杂度分析：

时间复杂度：O(NM)

空间复杂度：O(N)

2.2.7. 输出各顶点的入度和出度

void printDevOfV(GraphByMatrix* pg, ElemType v)

void printDevs(GraphByMatrix* pg, ElemType v)

无返回值，传入邻接矩阵，无意义参数v（故意构造这个参数列表，后面可以用函数指针数组节省代码长度）

步骤：

循环n次，调用printDevOfV函数，传入邻接矩阵和顶点
获取顶点下标，计算其入度边数和出度边数，在这里要区分无向图和有向图~

复杂度分析：

时间复杂度：O(N)

空间复杂度：O(1)

2.2.8. Floyd 算法求每对顶点之间的最短路径；

void floydWarShall(GraphByMatrix* pg, int** dist, int** path);

void printMinPaths(GraphByMatrix* pg, ElemType v);

无返回值，传入邻接矩阵，无意义参数v（故意构造这个参数列表，后面可以用函数指针数组节省代码长度）

步骤：

定义二维数组dist和二维数组path
掉头floydWarShall函数，传入这些参数，在这个函数中，首先要对二维数组初始化
在经历三层循环（最外层循环是中间节点），进行n³次松弛
循环结束返回到printMinPaths函数，循环n次调用printPath函数打印每一个顶点的最短路径
最终释放临时资源

复杂度分析：

时间复杂度：O(N³)

空间复杂度：O(N²)

2.2.9. 主函数菜单和测试设计

#include "basis.h"


void menu1() {
	printf("***************************\n");
	printf("0. 退出\n");
	printf("1. 有向图示例\n");
	printf("2. 无向图示例\n");
	printf("***************************\n");
}

void menu2() {
	printf("***************************\n");
	printf("0. 退出\n");
	printf("1. 输出邻接矩阵\n");
	printf("2. 输出邻接表（出度表）\n");
	printf("3. DFS\n");
	printf("4. BFS\n");
	printf("5. 获取最小生成树\n");
	printf("6. 获取最短路径\n");
	printf("7. 获取顶点的入度和出度\n");
	printf("8. 获取多元最短路径\n");
	printf("***************************\n");

}
void test(char* file) {
	GraphByMatrix* pg1 = createMByFile(file);
	GraphByList* pg2 = createLByFile(file);
	void(*p[])(GraphByMatrix*, ElemType) = {
		NULL, NULL, NULL, dfs, bfs, prime,
		printMinPath, printDevs, printMinPaths
	};
	int input = 0;
	do {
		ElemType V = 'A';
		menu2();
		scanf("%d", &input);
		if (input < 0 || input > 8) {
			printf("请重新输入");
			continue;
		}
		switch (input) {
			case 0 :
				printf("退出成功\n");
				break;
			case 1:
				printMatrix(pg1);
				break;
			case 2:
				printList(pg2);
				break;
			default:
				printf("输入起始点:");
				do {
					scanf("%c", &V);
				} while (V == '\n' || V == ' ');
				
			case 7:
			case 8:
				p[input](pg1, V);	
				printf("\n");
				break;
		}
	} while (input);
}

int main() {


	int input = 0;
	do {
		menu1();
		scanf("%d", &input);
		switch (input) {
			case 0:
				printf("退出成功\n");//由于此次后程序就结束了，所以就不free了
				break;
			case 1:
				test("有向图.txt");
				break;
			case 2:
				test("无向图.txt");
				break;
			default:
				printf("请重新输入\n");
				break;

		}

	} while (input);

	return 0;
}