前缀树（prefix tree）
准备一个Str[]，数组中元素有[“abc”,“bcd”,“abg”,“bcde”,“qwe”]，如何将数组中元素加到树中呢？
从最开始的字符串abc说，第一个字符是a，从一个空的头节点出发，看有没有走向a字符的路，没有，就创建一条，字符不放在节点上，字符永远在路上，b也同理，从a节点出发，没有b的就创建，最终创建出来的就是下图这样。

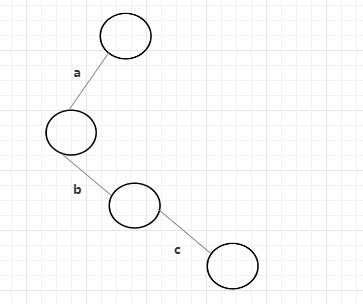
后面的字符串原理相同，从头节点出发，看有没有走向该字符的路，有就复用没有则创建，所以根据上面的数组构建出来的前缀树是这样的。

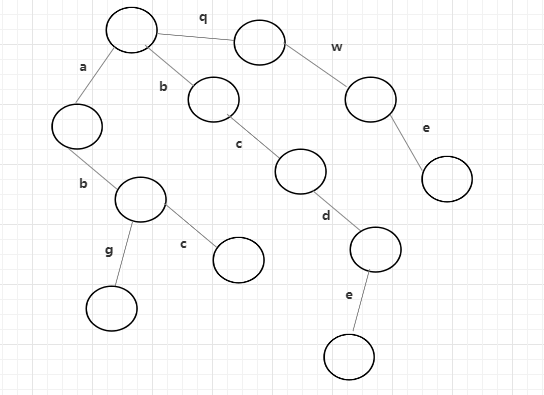
所以可以看出来，前缀树是一课多叉树
因为前缀树中，节点不存放值，所以封装一些额外的信息属性，比如说pass(构建树的过程中，该节点经过几次)，end(当前节点，有多少字符串以它结尾)。根据上面数组中的例子，算下来每一节点的情况是这样。

树构建完之后，就可以根据这个树的结构查看是否以xxx开头的字符串，以及树中是否存在xxx字符串。

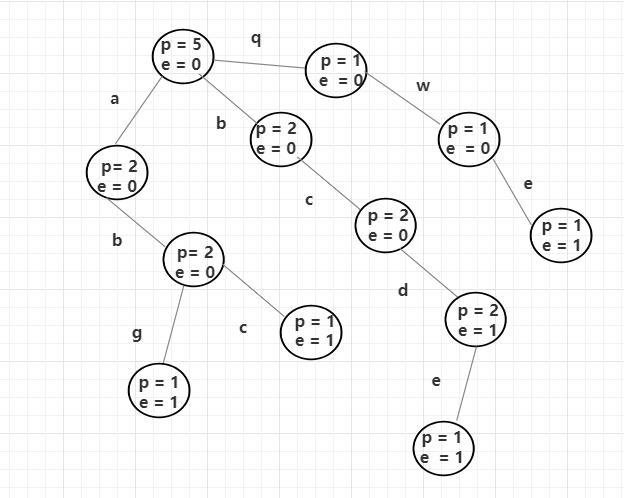
所以说，前缀树的结构，比hash表结构强的地方就在于，前缀树可以查找树中是否存在以xxx开始的前缀字符串。

Hash表
之前的帖子中说过，hash表的增删改查都是O(1)的常数时间操作，但前提是不考虑单样本量大小的情况下。
如果说添加的都是32位的整型Int类型数字，那不用考虑，但如果添加的是一个很大的字符串（这个字符串存着一本书的内容）。那此时就不是O(1)的长度。是O(K)的操作（K = 字符串长度）。
所以说，如果往Hash表中添加数据，如果单样本大小无足轻重，则认为是O(1)，如果单样本很大，那就不是O(1)，因为Hash表会遍历字符串的长度计算出Hash值才知道自己再hash表中如何组织，添加100W个字符串，平均长度是100，那Hash表单次添加就是O(100)的复杂度。
添加对象也是O(1)操作，因为添加的是对象内存地址。

Java代码实现

public static class Node {
        private int pass;
        private int end;
        private Node[] nexts;
        //private HashMap<Integer,Node> nexts;

        public Node() {
            pass = 0;
            end = 0;
            //表达下层有多少路
            //先以26个小写英文字母为例，所以长度为26 a - z
            //用底层节点是否为null,标记这条路是否存在。
            // 0   a
            // 1   n
            // 2   c
            //25   z
            //nexts[i] == null  i方向的路不存在
            //nexts[i] != null  i方向的路存在
            nexts = new Node[26];
            //如果字符种类多，则用上面的hashMap存储，key 就是字符的ascII转成数字的形式。
        }
    }

    public static class Trie {
        private Node root;

        public Trie() {
            root = new Node();
        }

        //遍历，将字符拆开，挂在树上
        public void insert(String str) {
            if (str == null) {
                return;
            }
            char[] tmp = str.toCharArray();
            Node node = root;
            node.pass++;
            int path = 0;
            //遍历字符
            for (int i = 0; i < tmp.length; i++) {
                //通过 - 'a' 来判断下一节点是否存在，如果存在下标是什么
                path = tmp[i] - 'a';
                if (node.nexts[path] == null) {
                    node.nexts[path] = new Node();
                }
                node = node.nexts[path];
                node.pass++;
            }
            node.end++;
        }

        //查询str在树中加入过几次
        public int search(String str) {
            if (str == null) {
                return 0;
            }
            char[] tmp = str.toCharArray();
            Node node = root;
            int path = 0;
            for (int i = 0; i < tmp.length; i++) {
                path = tmp[i] - 'a';
                if (node.nexts[path] == null) {
                    return 0;
                }
                node = node.nexts[path];
            }
            return node.end;
        }

        //树中有多少以str作为前缀的
        public int prefixNumber(String str) {
            if (str == null) {
                return 0;
            }

            Node node = root;
            char[] tmp = str.toCharArray();
            int path = 0;
            for (int i = 0; i < tmp.length; i++) {
                path = tmp[i] - 'a';
                if (node.nexts[path] == null) {
                    return 0;
                }
                node = node.nexts[path];
            }
            return node.pass;
        }

        //删除树中str字符串
        public void delete(String str) {
            //先确定要删除的字符串在树中存在，要不减完发现不存在就淦了
            if (search(str) != 0) {
                char[] tmp = str.toCharArray();
                Node node = root;
                node.pass--;
                int path = 0;
                for (int i = 0; i < tmp.length; i++) {
                    path = tmp[i] - 'a';
                    if (--node.nexts[path].pass == 0){
                        //避免内存泄漏，先--,如果是0，则后面的直接都干掉。
                        node.nexts[path] = null;
                        return;
                    }
                    node = node.nexts[path];
                }
                node.end--;
            }
        }
    }