第11章 Fourier变换(Transform)

11.1 引言

11.2 逆向正弦和余弦变换(The Inverse Cosine and Sine Transforms)

11.3 正向正弦和余弦变换(The Forward Cosine and Sine Transforms)

11.4 离散谱对比谱密度(Discret spectra vs. spectral density)

11.5 Fourier变换的复数形式

11.6 Fourier定理

11.7 复数和三角Fourier变换之间的关系

第11章 Fourier变换(Transform)

11.1 引言

前几章描述的Fourier分析方法的定义域是3类函数：具有有限个值的离散数据向量、具有无限个值的离散向量和限定在有限区间内的连续函数。这些分别是如图 5.1 所示的情况 1、2 和 3。第4种情况允许定义在无限区间内的连续函数。这是Fourier变换的领域。

学生可能很想知道，当任何“现实世界(real world)”的函数仅可以在有限的距离之上、或者针对有限的时长进行观察的时候，为什么能够对定义在无限范围内的函数进行Fourier叶分析,，并且为什么这种分析又十分重要。可以提供几个原因。首先，案例 4 非常笼统，它涵盖了其他 3 个案例。因此，Fourier变换为各种问题提供了统一的方法，其中许多问题只是更一般公式的特例。其次，物理系统通常由具有无限范围的连续函数建模。例如，点光源的光学图像在理论上可以用 $e^{-x^{2}}$ 形式的Gauss函数来描述，它对所有 x 都存在。另一个例子是一桶水底部的水龙头流出的水流速度，可以建模为 $e^{kt}$ 。如果我们有能力处理在所有时间或空间上定义的函数，则可以通过频谱分析获得对此类系统的行为的新见解。 第三，Fourier分析方法通过消除情况 3 中连续函数仅存在于有限区间内的限制，从而发展成为一种非常强大的分析工具，已在科学和数学的许多分支中证明是有用的。

11.2 逆向正弦和余弦变换(The Inverse Cosine and Sine Transforms)

我们的Fourier变换方案(情况4)将是对我们先前对有限区间上连续函数分析的结果(情况3)的推广结果。在第6章(译注：连续函数的Fourier分析)中，我们求得任意实数函数 y(x) 都可以用一个具有无穷多个构成项的 Fourier 级数准确地表示。假如 y(x) 定义在开区间(-L/2,L/2)上，则其Fourier模型是

$y(x) = \frac{a_0}{2} + \sum_{k=1}^{+\infty}[a_k cos(\frac{2\pi kx}{L})+b_k sin(\frac{2\pi kx}{L})]$ ---------------------------------[11.1]

(译注：实际上 $\frac{2\pi}{L} = \omega$ ，表示角频率，即单位时间转过的角度，单位弧度。k表示谐波的第k项，x 为区间内的变量。)

正如等式[4.2]所定义，这个模型的基波频率是 Δ f = 1/L ，并且，所有更高次谐波的频率 $f_k$ 都是基波频率的整数倍(译注：谐波，和声的波，相对于无规律的噪音而言，其高次波频率必定是基波频率的整数倍，这正是谐波的特点)。即， $f_k = k\Delta f = k/L$ 。现在我们面临着这种境况(prospect)——令 L → ∞ ，就意味着Δ f → 0，因此谐波频率的概念对这种情况将不再有用。

为了挽救这种局面，我们需要区分(disassociate)物理频率和谐波数的概念。为此，我们首先更改符号，以便我们可以将Fourier系数视为频率变量 $f_k$ 的函数，该频率变量 $f_k$ 的离散值是 Δ f 的倍数。因此等式[11.1]变成

$y(x) = \frac{a(0)}{2} + \sum_{k=1}^{+\infty}[a(f_k) cos({2\pi xf_k})+b(f_k) sin({2\pi xf_k})]$ --------------[11.2]

接下来，为了解决极小的Δ f 带来的困难，我们将等式右侧的每一项乘以量Δ f /Δ f 。于是，得到

$y(x) = \frac{a(0)}{2\Delta f} \Delta f+ \sum_{k=1}^{+\infty}\left \{ [\frac{a(f_k) }{\Delta f}cos({2\pi xf_k})]\Delta f+\frac{b(f_k)}{\Delta f} sin({2\pi xf_k})]\Delta f\right \}$ ------[11.3]

这个等式表明，要在任何特定的 x 值下计算函数 y(x)，我们需要将无限多的项相加，其中一项是常数，其他项是加权三角函数值。图 11.1 中突出显示了这些有助于求和的三角函数值之一。

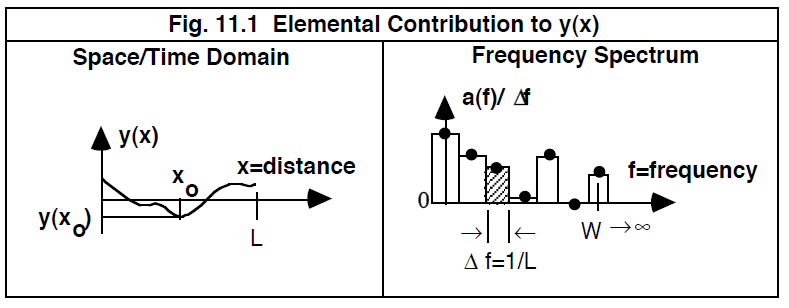
------------------------------------图 11.1 对 y(x)的元素贡献-------------------------------------------

在图中的右侧图中，纵坐标是Fourier系数的幅度除以频谱的频率分辨率(frequency resolution)。因此，将这种形式的Fourier谱视为幅度密度(amplitude density)图是合适的。这是观点上的一个关键变化，因为现在交叉影线矩形的面积(而不是纵坐标值)表示模型的这个特定三角分量的幅度 $a_k$ 。

从这个新的观点来看，等式中[11.3]的两个求和表示离散曲线下的面积。这通过考虑 x = 0 的例子最容易看出，在这种情况下 cos(2π f x) = 1 等式[11.3]中的中间项表示图 11.1 中光谱中所有矩形的组合面积。这种解释也适用于 x 的其他值，唯一的区别是矩形的高度在计算它们的面积之前由 cos(2π f x)调制。因此，很明显，在 Δf → 0 的限制下，等式[11.3] 中的求和项成为表示平滑曲线下面积的积分。也就是说，我们基于以下等式隐式定义了两个新函数 C( f ) 和 S( f )

$\lim\limits_{\Delta f \to 0}[\frac{a(f_k) }{\Delta f}cos({2\pi xf_k})]\Delta f = \int_{0}^{+\infty}{C(f)cos(2\pi xf)df}$

$\lim\limits_{\Delta f \to 0}[\frac{a(f_k) }{\Delta f}sin({2\pi xf_k})]\Delta f = \int_{0}^{+\infty}{S(f)sin(2\pi xf)df}$ -------------------[11.4]

总之，函数 C( f ) 和 S( f ) 表示当 Δf 接近零时幅度密度函数(分别针对Fourier频谱的余弦和正弦部分)的极限情况。鉴于这些定义，我们可以得出结论，在Δf → 0 时等式 [11.3] 的极限变成

$y(x)= \int_{0}^{+\infty}{C(f)cos(2\pi xf)df}+\int_{0}^{+\infty}{S(f)sin(2\pi xf)df}$ -------------[11.5]

该结果是三角形式的Fourier逆变换方程。 它定义了如何从两个谱密度函数 C( f ) 和 S( f ) 重构连续函数 y(x)。接下来给出确定给定函数 y(x) 的这些谱密度函数的方法。

11.3 正向正弦和余弦变换(The Forward Cosine and Sine Transforms)

为了指定正向Fourier变换，我们更进一步地考察极限表达式中Fourier系数 $a_k$ 和 $b_k$ 的行为。要做这样的分析，我们回顾等式[6.5]中给出的 $a_k$ 的定义

$a_k = \frac{2}{L} \int_{-L/2}^{L/2}y(x)cos(2\pi kx/L)$ ----------------------------------[11.6]

此等式对所有k的取值都成立，包括取值为0 。代入Δ f = 1/L 和 $f_k = k/L$ ，我们得到

$\frac{a_k}{\Delta f} = 2\int_{-L/2}^{L/2}y(x)cos(2\pi xf_k)dx$ ---------------------------------[11.7]

(译注：上式中两边乘以周其L )

当 L → ∞ 时，离散谐波频率 1/L ，2/L，等等，连了一个连续体，且比率 $a_k/\Delta f$ 成了一个频率的连续函数，称为 C( f ) 。类似地，比率 $b_k/\Delta f$ 成了一个频率的连续函数，称为 S( f )。即，以极限表达，为

$C(f) = 2\int_{-\infty}^{\infty}y(x)cos(2\pi xf)dx$

$S(f) = 2\int_{-\infty}^{\infty}y(x)sin(2\pi xf)dx$ --------------------------------[11.8]

函数C( f )和 S( f ) 分别称为函数 y(x) 的余弦Fourier变换(cosine Fourier transform)和正弦Fourier变换 (sine Fourier transform)。请注意，对于具体的 f = 0 (在等式11.5中，这种情况解释为缺乏显式常量项)这种情况，两个等式都是有效的。

11.4 离散谱对比谱密度(Discret spectra vs. spectral density)

为了帮助理解从Fourier级数到Fourier变换的过渡，请考虑图 11.2 中定义的函数。该脉冲定义在长度等于一秒的长度间隔内。脉冲的Fourier级数可以在参考书中找到，也可以很容易地用手计算为

$v(t) = \frac{1}{2} + \frac{2}{\pi} [cos(2\pi t)- \frac{1}{3} cos(3.2\pi t) + \frac{1}{5} cos(5.2\pi t) - ...]$ -------------------[11.9]

-------------------------------------------图11.2 短窗脉冲频谱------------------------------------------------

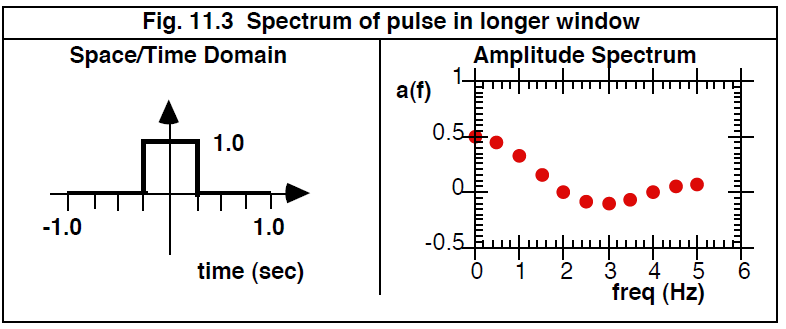
现在，如果观察间隔加倍而不改变脉冲持续时间，如图 11.3 所示，我们有新的Fourier级数

$v(t) = \frac{1}{4} + \frac{2}{\pi} [0.707cos(\pi t)- \frac{1}{2} cos(2\pi t) + \frac{0.707}{3} cos(3\pi t) - ...]$ --------[11.10]

-------------------------------图11.3 长窗脉冲频谱-----------------------------------------------------

请注意，正如预期的那样，图 11.3 中相同物理带宽中的谐波数量是图 11.2 的两倍，而图 11.3 中相应分量的幅度是图 11.2 的一半。因此，如果我们进一步增加观察间隔，Fourier系数将继续下降，并且随着观察间隔任意增大而变得非常小。为了挽救频谱的概念，我们应该绘制谱密度函数 a ( f )/Δf。 通过除以Δf，我们有效地补偿了延长的间隔，因此无论观察间隔的长度如何，光密度函数都保持不变。

-------------------------------图11.4 在无限窗上的脉冲频谱---------------------------------------

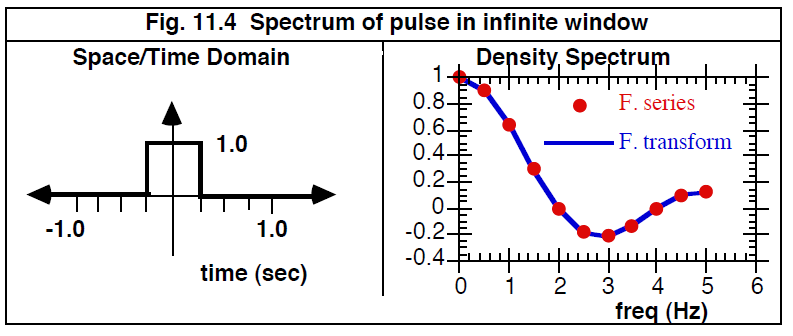
现在让我们计算一个单位高度和宽度为 w 的脉冲的正式Fourier变换，该脉冲定义在无限区间内，如图 11.4 所示。应用等式 [11.8] 我们有

$C(f) = 2\int_{-\infty}^{\infty}y(x)cos(2\pi xf)dx$

$= 2\int_{-\infty}^{-w/2}0.cos(2\pi xf)dx+\int_{-w/2}^{w/2}1.cos(2\pi xf)dx+\int_{w/2}^{+\infty}0.cos(2\pi xf)dx$

$=4\int_{-w/2}^{w/2}1.cos(2\pi xf)dx$

$=\frac{sin(2\pi xf)}{2\pi f}|_{0=0}^{x=w/2}$

$=2\frac{sin(\pi f w)}{\pi f}$ -----------------------------------------------------------------[11.11]

这种形式的结果在Fourier分析中经常出现，从而导致了特殊函数sinc(x) = sin(πx)/πx 的定义(译注：sinc[sɪŋk],为拉丁语“sinus cardinalis”的简写，由Phillip M. Woodward 于 1953 年首次引入)。因此最后的结果是

C( f ) = 2wsinc(wf ) --------------------------------------------------------[11.12]

w = 0.5 正是当前的例子。

在 2 秒内看到的脉冲的归一化Fourier级数 a(f)/Δf 。图 11.4 中的窗口与在无限窗口中看到的同一脉冲的余弦Fourier变换进行了比较。请注意，连续Fourier变换对离散频谱进行了插值。这是一个概念的例子，即Fourier变换是一种更通用的工具，将Fourier级数作为一种特殊情况包含在内。

11.5 Fourier变换的复数形式

尽管前面的发展有助于直观地理解从Fourier级数到Fourier变换的转变，但由此产生的等式主要具有其历史意义，因为现代作者总是选择以复数形式表示Fourier变换。现在以等式[6.6]中给出的复数Fourier级数的基本公式开始。

$y(x)=\sum_{k=-\infty}^{+\infty}c_ke^{i(2\pi kx/L)}$ -----------------------------------------------------[6.6]

我们可以遵循上面采用的方法。引入必要的变量改变，并乘以Δf/Δf ，在极限表达式中，随着Δf → 0 , 这个等式就成了逆Fourier变换

$y(x) = \int_{-\infty}^{+\infty}Y(f)e^{i(2\pi xf)}df$ ----------------------------------------------------[11.13]

其中，Y( f ) 是函数y( x )的复频率谱。

为了获得正向变换，我们从有限连续函数的复数Fourier系数的定义开始

$c_k=\frac{a_k-ib_k}{2}$

$= \frac{1}{L}\int_{-L/2}^{+L/2}y(x)e^{-i(2\pi kx/L)}dx$ ------------------------------------------------[6.7]

当 L → ∞ 时，离散谐波频率 1/L ，2/L，等等，连了一个连续体，且比率 $c_k/\Delta f$ 成了一个频率的连续函数，称为 Y( f ) 。因此，正向Fourier变换定义为等式

$Y( f ) = \int_{-\infty}^{+\infty}y(x)e^{-i(2\pi xf)}dx$ ----------------------------------------------[11.14]

通过观察等式 [11.13] 和 [11.14] 之间惊人的相似性，学生可能会开始理解复数形式的Fourier变换运算流行的原因之一。正向变换和逆向变换之间的唯一区别是复指数中指数的符号。这个指数项称为被积函数的内核(kernel)，因此我们观察到正向和逆向变换的内核是彼此的复共轭(complex conjugate)。 复数形式相对于三角函数形式的另一个优点是只需要指定和求解一个积分而不是两个。 最后，也是最重要的，即使函数 y(x) 是复数值函数，这个变换的复数形式也适用。