🎭不要管上面那玩意。。。

引入

现在，你，是一位酒店的经理。

西装笔挺，清瘦智慧。

金丝眼镜，黑色钢笔。

大理石的地板，黑晶石的办公桌，晶莹的落地玻璃。

而现在，有几个雍容华贵的贵妇要入住你的酒店，她们各有一些要求。

请你最大限度地满足她们的要求。

这，就是二分图最大匹配的一个现实问题（《非诚勿扰》也是一种）

前置知识

链式前项星

链式前向星是一种图的存储结构，它以链表形式存储每个顶点的出边信息，其中每个节点的结构如下：

struct Edge {
    int to, next;
};

其中，to表示该边指向的顶点编号，next表示与该顶点相邻的下一个顶点在链表中的位置。因此，链式前向星可以使用一个数组来存储每个顶点的邻接链表，如下所示：

const int N = 1e5 + 10;

// head[i]表示顶点i的邻接链表的头结点在edges数组中的下标
int head[N];

// edges数组用来存储所有顶点的出边信息，其中的每个元素表示一个边
Edge edges[N];

因为在链式前向星中，一个顶点的出边被存储在链表中，因此需要指定每个顶点邻接链表的头结点在edges数组中的位置。当需要访问该顶点的出边信息时，只需要从该链表的头结点开始遍历即可。

下面，我们来看一下链式前向星的代码实现。假设我们需要构建一个无向图，其中有n个顶点和m条边，那么可以使用以下代码来构建邻接链表：

void addEdge(int u, int v) {
    edges[cnt].to = v;
    edges[cnt].next = head[u];
    head[u] = cnt++;

    edges[cnt].to = u;
    edges[cnt].next = head[v];
    head[v] = cnt++;
}

void init() {
    memset(head, -1, sizeof(head));
    cnt = 0;
    for (int i = 0; i < m; i++) {
        int u, v;
        cin >> u >> v;
        addEdge(u, v);
    }
}

在上述代码中，addEdge函数用于向无向图中添加一条边。因为是无向图，所以需要同时添加两条边，一条从u到v，一条从v到u。在添加边的过程中，需要在edges数组中存储两个结构体分别表示这两条边的信息，并将它们分别添加到u和v的邻接链表的头部。

初始化函数init则用于初始化head数组和cnt变量。在函数中，head数组被初始化为-1，表示所有顶点的邻接链表都为空。cnt变量则表示当前已经添加的边的数量，一开始初始化为0。

使用链式前向星可以实现高效的图算法，比如深度优先遍历和广度优先遍历。因为链式前向星只存储与每个顶点相邻的边，所以可以避免遍历不必要的边，提高算法的运行效率。

二分图

二分图是指一个无向图的所有顶点可以被分为两个互不相交的子集，使得同一子集内的顶点之间没有边相连。也可以说，如果将图中的顶点分为两个集合，那么图中所有的边都是将一个集合中的顶点与另一个集合中的顶点相连。这种图形状就像是将顶点分为两个颜色，每个颜色内的顶点之间没有边相连，而不同颜色的顶点之间都有边相连。

举个例子，可以将需要交际的人分为两个集合A和B，A集合中的人互相认识，B集合中的人也互相认识，但是A集合中的人与B集合中的人互相不认识。用图来表示的话，就是将A集合中的每个人与B集合中的每个人之间连一条边。

二分图有许多应用，比如匹配问题、调度问题、最大独立集、任务分配等。其中最常见的应用是匹配问题，即给定一个图，找到图中的最大匹配，也就是寻找一种方案，使得图中的最多的边满足两端都是不同颜色的顶点。

最大匹配

 最大匹配：选出的子集包含边的个数最大。

 举个例子：

在下图中，无论如何画都无法匹配出超过三对，3就是最大匹配。

 （红边表示被匹配的边）

模板题目

【模板】二分图最大匹配

题目描述

给定一个二分图，其左部点的个数为 n，右部点的个数为 m，边数为 e，求其最大匹配的边数。

左部点从 1 至 n 编号，右部点从 1 至 m 编号。

输入格式

输入的第一行是三个整数，分别代表 $n$，$m$ 和 $e$。

接下来 e 行，每行两个整数u, v，表示存在一条连接左部点 u 和右部点 v 的边。

输出格式

输出一行一个整数，代表二分图最大匹配的边数。

样例

#1

输入
1 1 1
1 1

输出 
1
 

#2

输入
4 2 7
3 1
1 2
3 2
1 1
4 2
4 1
1 1

输出
2

提示

数据规模与约定

对于全部的测试点，保证：

• 1≤n,m≤500
• 1≤e≤5×
• 1≤u≤n,1≤v≤m。

不保证给出的图没有重边。

 题目很简洁，就不进行分析了。向下看，看这题怎么解。

算法原理

下面采用一种 喜 闻 乐 见 的方式进行演示。

突然发现上面的引入太无聊了，那么就换个例子吧。

既然是匹配，那就来找女朋友……

😍😍😍😍😍😍😍😍😍😍😍

图文趣味演示

图片用的是我中学同学的。

点集是这样的

（为何B 集还有♂的？经费有限。。。）

至于边集 ，随便连几条线吧。

 用数据表示出来就是这样。（输入）

5 5 8

1 6

1 8

1 10

2 7

3 9

3 10

4 9

5 6 

（关于输入格式，自行看上面的模板题目部分）

然后，我们设：

vis[i]存B集i号点是否被访问。

match[i]存与i配对的点的编号。

好，开始游戏。

首先看1号点。

第一个找到的就是6号点，那么就将match[1]=6,match[6]=1，配对成功。

然后是二号点，很显然，他只能找7号，那就配对吧。match[2]=7,match[7]=2;

三号，是9号。

至此，图是这样。（红色边连接配对两点）

 之后，到了4号点。

他也选择9号点，但已经被3号选择了，他就问3号，你可以把9好让出来吗？

3号备胎多心胸广大，就搜索自己其他的边。找到了，那就告诉4号，可以。因此，3号便换成了10号，4号换成了9号。

………………

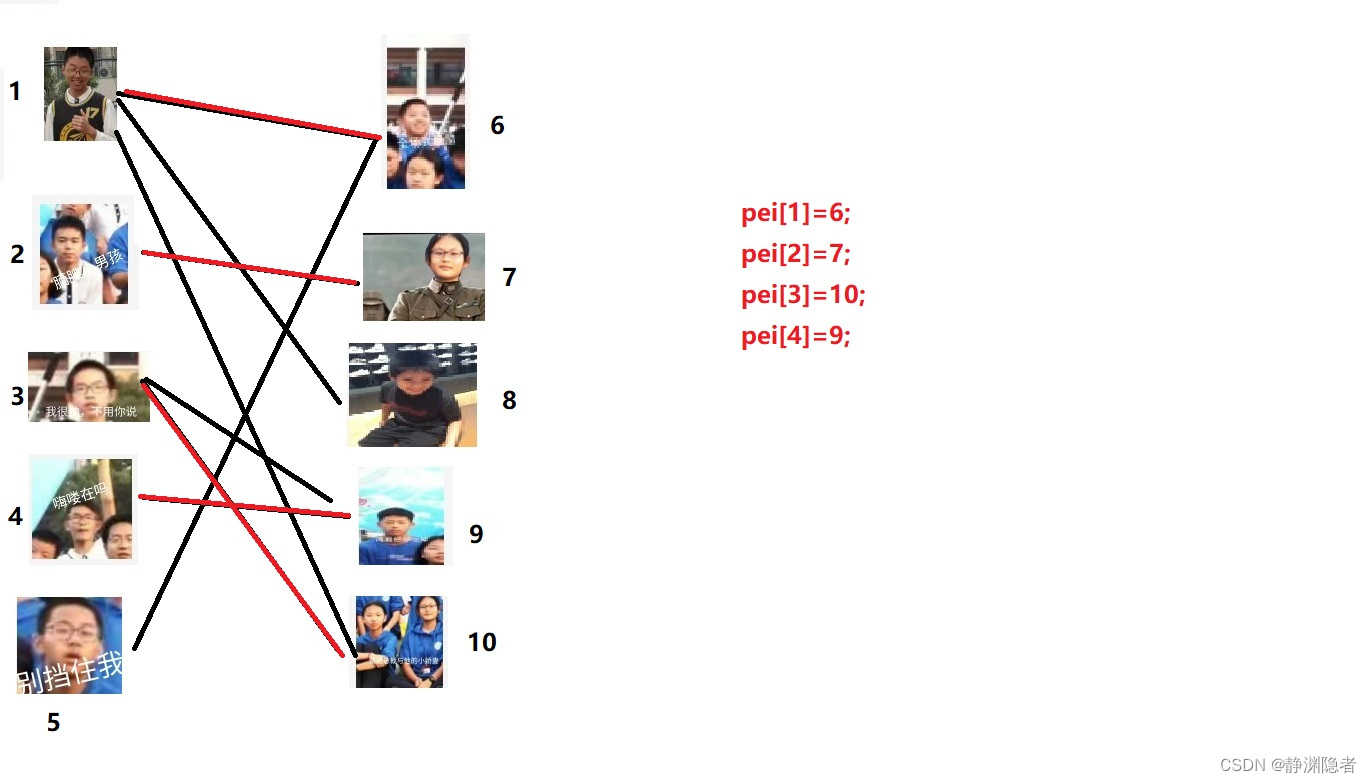
最后，成了这样。

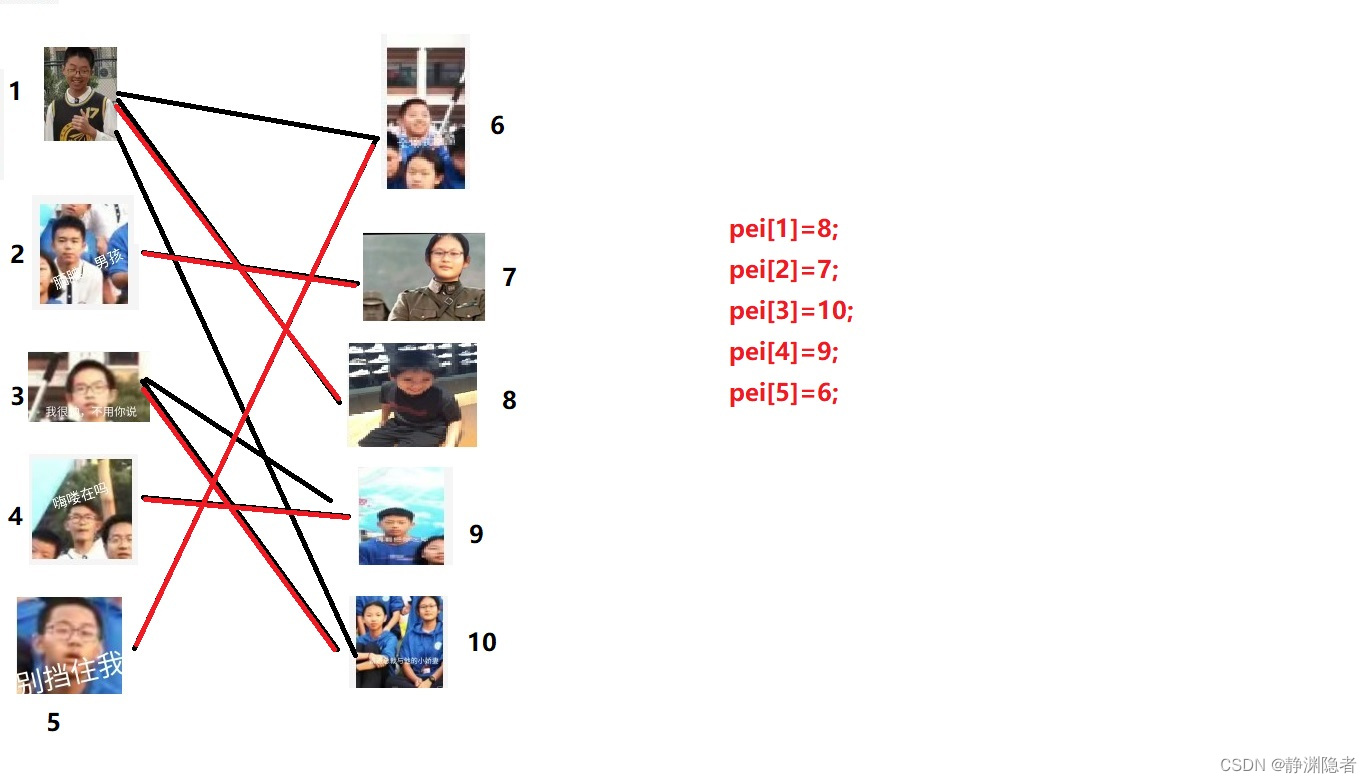
 因此，该图的最大匹配为5。

据此易得，有如下几个步骤。

1.依次遍历个点

存图之后，就用for循环对A集合的点进行遍历。

每到一个点，就清空vis数组，进行dfs操作。

2.递归寻找匹配者

若此人没有匹配，或者其匹配者可以让出，就匹配成功，返回true。

否则，若遍历其所有出边都找不到，返回false。

代码如下：

bool dfs(int x)
{
	for(int k=last[x];k;k=e[k].pre)
	{
		int y=e[k].y;
		if(vis[y]) continue;
		vis[y]=true;
		if(!match[y]||dfs(match[y]))
		{
			match[y]=x;
			return true;
		}
	}
	return false;
}

代码

#include<bits/stdc++.h>
using namespace std;
const int N=10010;
struct edge{
    int x,y,pre;
}e[200010];
int last[N],elen=0,ans;
int n,m;
int vis[N],match[N];
void init(int x,int y)
{
	e[++elen]=edge{x,y,last[x]};
	last[x]=elen;
}
bool dfs(int x)
{
	for(int k=last[x];k;k=e[k].pre)
	{
		int y=e[k].y;
		if(vis[y]) continue;
		vis[y]=true;
		if(!match[y]||dfs(match[y]))
		{
			match[y]=x;
			return true;
		}
	}
	return false;
}
int main()
{
	int ll;
	scanf("%d%d%d",&n,&m,&ll);
	for(int i=1;i<=ll;i++)
	{
		int x,y;
		scanf("%d%d",&x,&y);
		init(x,y);	
	}
	for(int i=1;i<=n;i++)
	{
		memset(vis,0,sizeof(vis));
		if(dfs(i))
		{
			ans++;
		}
	}
	printf("%d",ans);
}