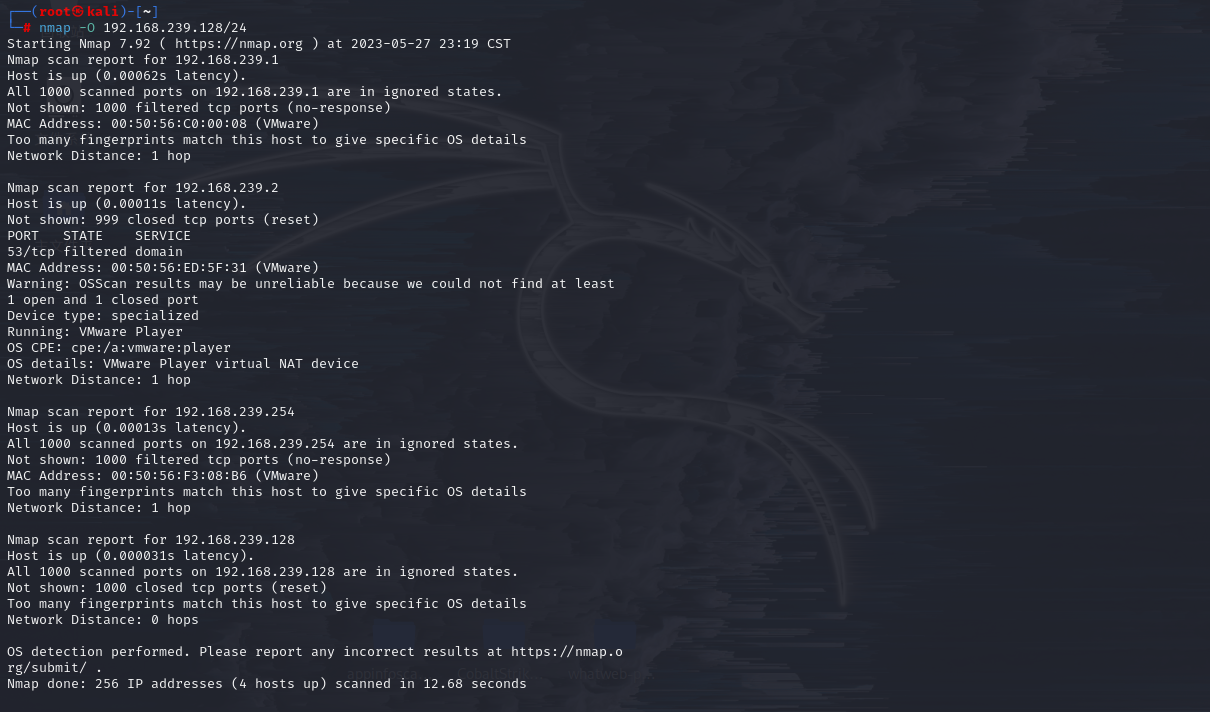
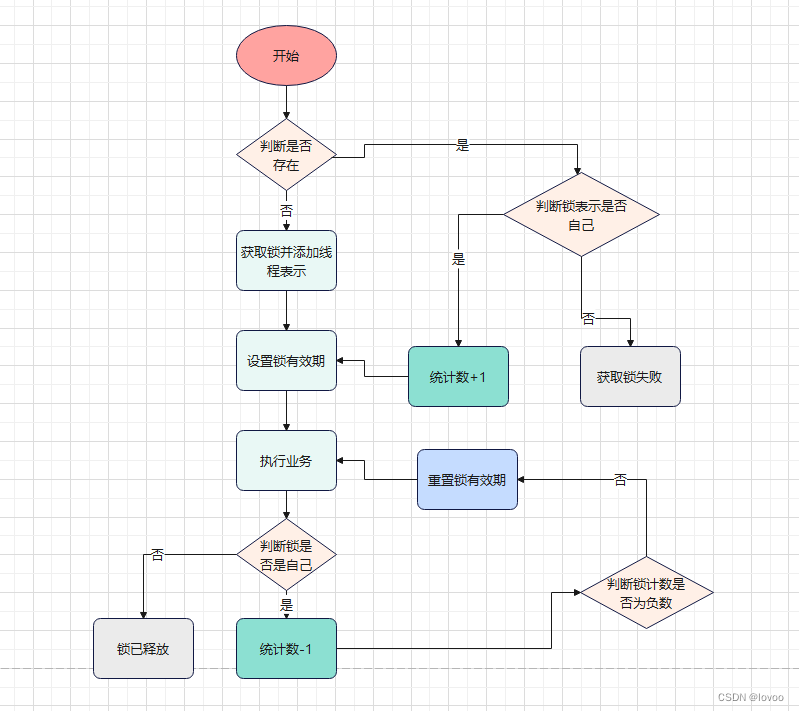
本文整理自哔哩哔哩视频:什么是奇异值分解SVD–SVD如何分解时空矩阵
📚奇异值分解是什么?
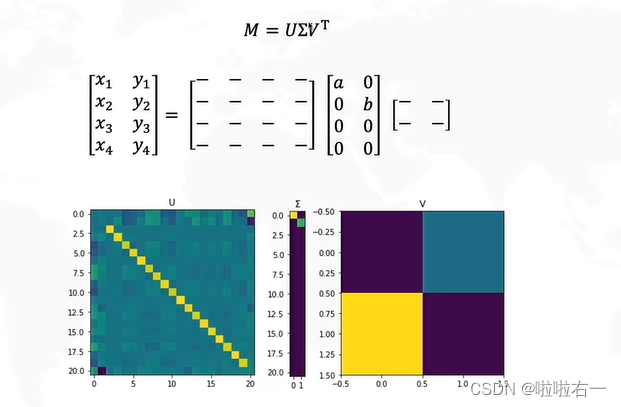
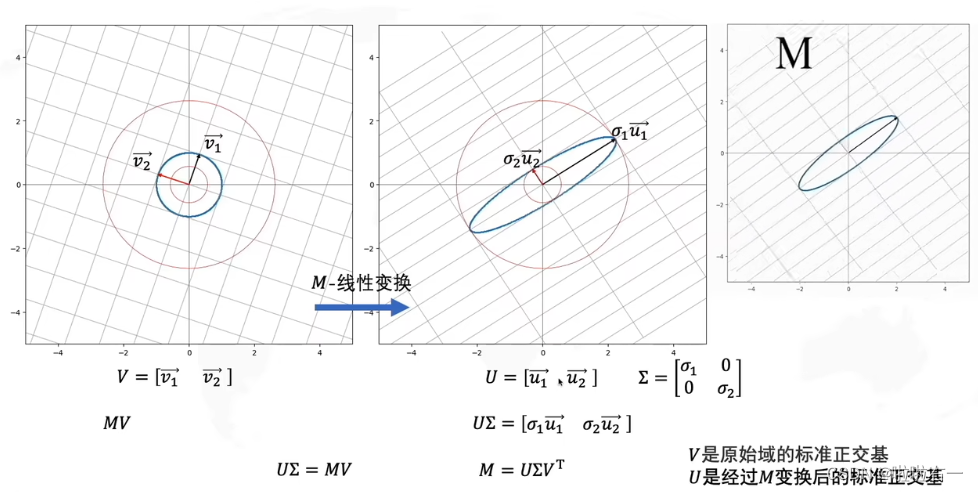
- M是原始矩阵,它可以是任意的矩阵,奇异值分解就是将它分解为三个矩阵相乘。
- U和V是方阵,∑是不规则矩阵,但其除了对角线其他位置都是0。
- SVD分解就是把M矩阵先旋转再拉伸再旋转。
- 如果是正交矩阵,那么它代表的意义就是旋转;
- 如果是对角矩阵,那么就是拉伸。

- V是原始域的标准正交基 ,U是经过M变换后的标准正交基。
📚奇异值分解应用
- SVD推广到任意大小矩阵
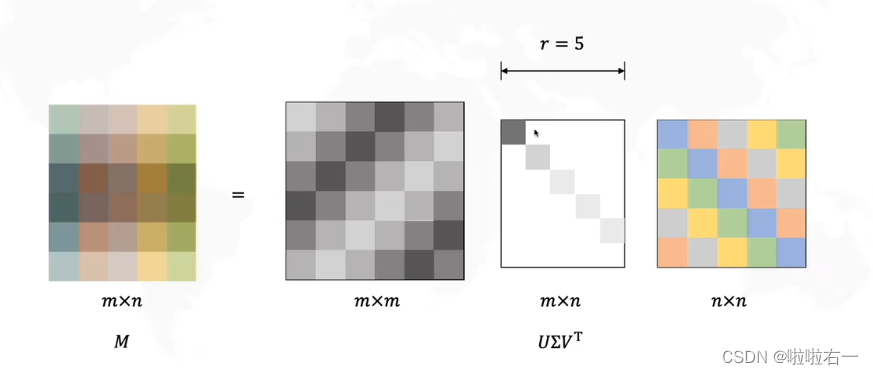
- 可以看到中间那一部分的最后一行其实是没有意义(都是0)的,所以可以做如下转化:
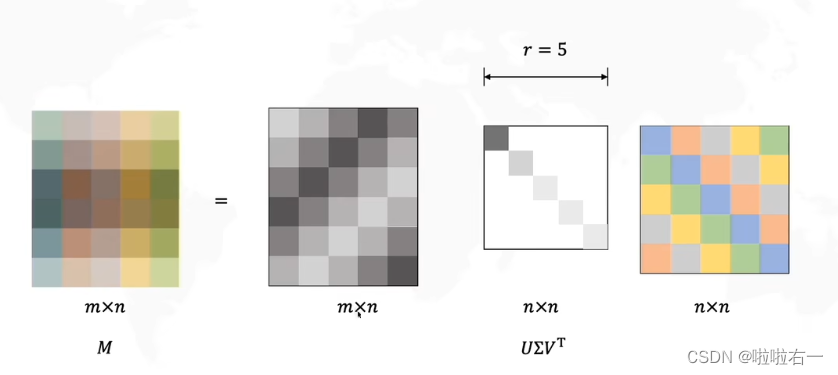
- 中间矩阵对角线上存的就是奇异值,并且是按从大到小排列的。然后将奇异值比较小的去掉,再转化:
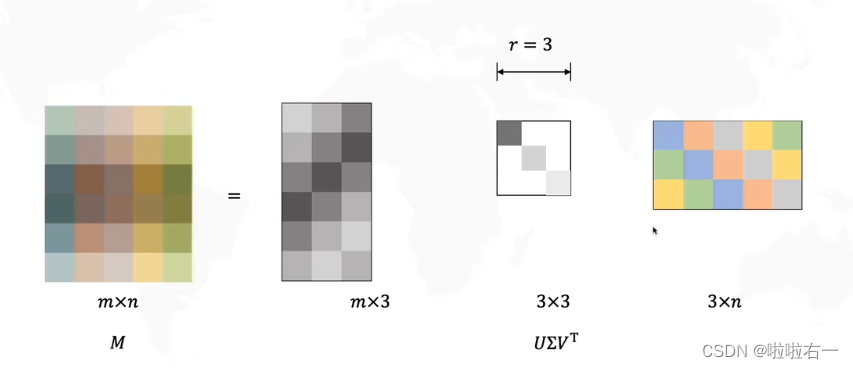
📚含义解释
- 上述转化后的结果可看作:

- 将UV相乘:

- 再把奇异值也相乘(可看作是盖了一层透明度),再叠加:


- 上图就是原始矩阵M,奇异值分解全过程即为:
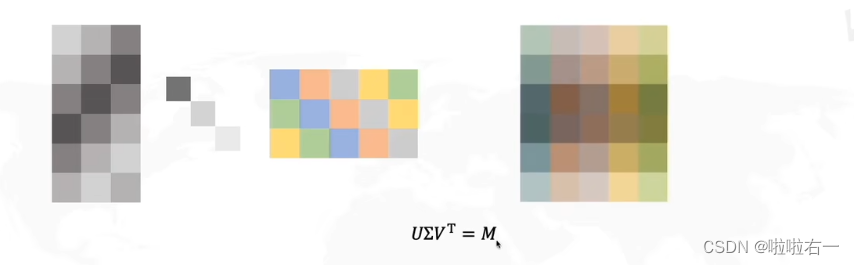
📚SVD分解时空矩阵
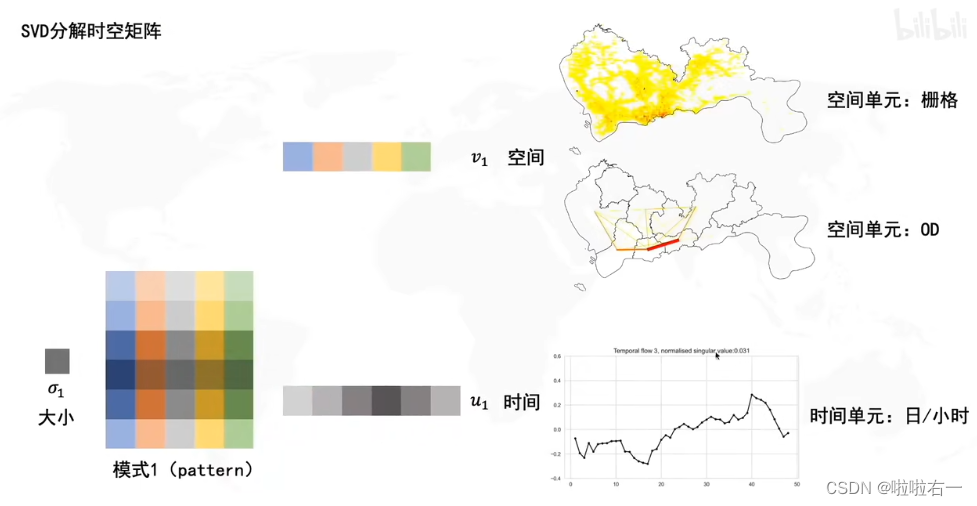
- 将原始的时空矩阵分解为时间空间都不同的不同模式:
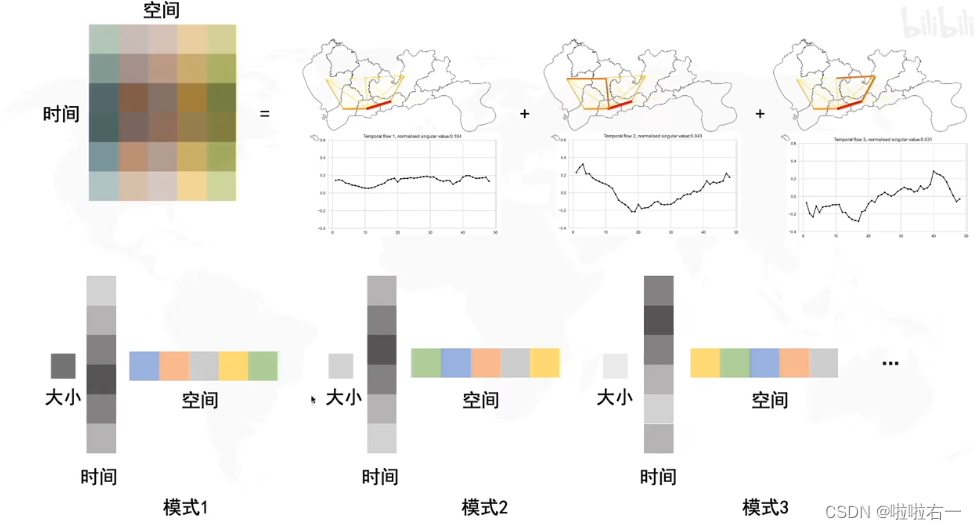
📚如何求SVD分解
该部分指路原视频13:14
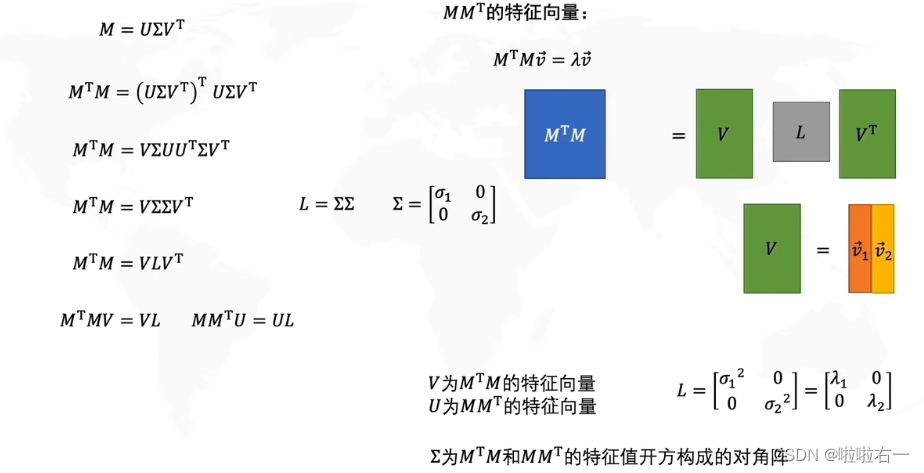

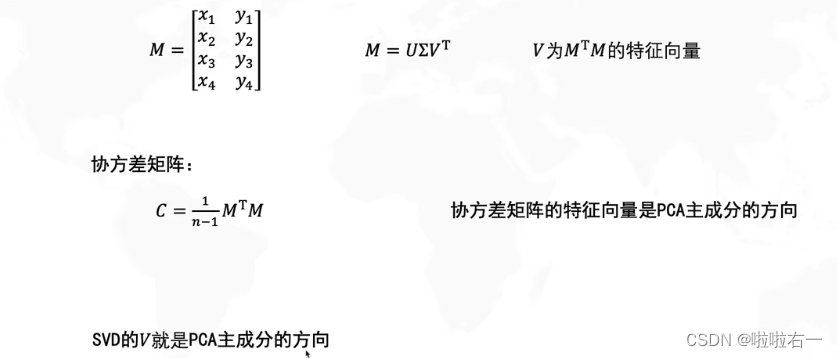
📚PCA的主成分与SVD的关系
wuwuwu,up讲得太好了!




![[元带你学: eMMC协议详解 10] Device 识别流程 与 中断模式](https://img-blog.csdnimg.cn/img_convert/262abfa94e2b5642120b21810384ce4b.png)