A:最小的数字
A-最小的数字_牛客小白月赛73 (nowcoder.com)
#include<bits/stdc++.h>
#define endl '\n'
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define int long long
using namespace std;
int n, m, k, A, B, N, M, K;
const int maxn = 1e6 + 10;
signed main()
{
int t;
cin >> t;
for (int i = t; 1; i++)
if (i % 3 == 0) return cout << i, 0;
return 0;
}B:优美的GCD
B-优美的GCD_牛客小白月赛73 (nowcoder.com)
#include<bits/stdc++.h>
#define endl '\n'
#define IOS ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
#define int long long
using namespace std;
int n, m, k, A, B, N, M, K;
const int maxn = 1e6 + 10;
void solve(){
cin >> n;
cout << n * 2 << " " << n << endl;
}
signed main()
{
int t;
cin >> t;
while(t--)
solve();
return 0;
}C:优美的序列
C-优美的序列_牛客小白月赛73 (nowcoder.com)
思维:其实
对于任意的 1≤i,j≤n1\leq i,j\leq n1≤i,j≤n,满足 ∣ai−aj∣≥∣i−j∣|a_i-a_j|\geq |i-j|∣ai−aj∣≥∣i−j∣。
只用满足n个不同的数字对其简单排序就可以了(大到小,或者小到大都可以)
干脆直接用一个set<int>来维护就可以了
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
int n, m, k, A, B, N, M, K;
const int maxn = 1e6 + 10;
void sove()
{
set<int>s;
bool is = false;
cin >> n;
while (n--)
{
cin >> m;
if (s.find(m) != s.end())is = true;
s.insert(m);
}
if (is) printf("-1\n");
else
for (auto i : s)
printf("%d\n", i);
}
int main()
{
cin.tie(0)->sync_with_stdio(false);
int t;
cin >> t;
while (t--)
sove();
return 0;
}D-Kevin喜欢零(简单版本)
D-Kevin喜欢零(简单版本)_牛客小白月赛73 (nowcoder.com)
E-Kevin喜欢零(困难版本)_牛客小白月赛73 (nowcoder.com)
DE不同点只在于数据不同,简单的说能过E就可以过D,这边直接用E的解了
#include <bits/stdc++.h>
#define endl '\n'
using namespace std;
const int maxn = 2e5 + 10;
int s2[maxn],s5[maxn];//存放第i个数分别有多少个2和5的因子
int n, m, k, t;
void solve()
{
for(int i = 0;i <= n; i++)s2[i] = s5[i] = 0;
cin >> n >> k;
for(int i = 1;i <= n;i++)
{
s2[i] = s2[i - 1];
s5[i] = s5[i - 1];
cin >> m;
for(int j = m;j % 2 == 0; j /= 2)s2[i]++;
for(int j = m;j % 5 == 0; j /= 5)s5[i]++;
}
long long ans = 0;
for(int i = 1;i <= n;i++)
{
int p2 = s2[i - 1] + k;
int p5 = s5[i - 1] + k;
int l2 = lower_bound(s2,s2 + n + 1, p2) - s2;
int r2 = upper_bound(s2,s2 + n + 1, p2) - s2;
int l5 = lower_bound(s5,s5 + n + 1, p5) - s5;
int r5 = upper_bound(s5,s5 + n + 1, p5) - s5;
int r = max(r2,r5), l = max(l2,l5);
l = max(i,l);
ans += r - l;
}
cout << ans << endl;
}
int main()
{
cin.tie(0) -> sync_with_stdio(false);
cin >> t;
while(t--)
solve();
return 0;
}核心代码
二分搜索范围到s + n + 1(+1的原因是因为第0个位置不是我们用于记数组因数,有效下标范围为[1,n])
long long ans = 0;
for(int i = 1;i <= n;i++)
{
int p2 = s2[i - 1] + k;
int p5 = s5[i - 1] + k;
int l2 = lower_bound(s2,s2 + n + 1, p2) - s2;
int r2 = upper_bound(s2,s2 + n + 1, p2) - s2;
int l5 = lower_bound(s5,s5 + n + 1, p5) - s5;
int r5 = upper_bound(s5,s5 + n + 1, p5) - s5;
int r = max(r2,r5), l = max(l2,l5);
l = max(i,l);
ans += r - l;
}
cout << ans << endl;解释:
对末尾有K个0可以转换成这个数是X * 10^K(其中X % 10 != 0)
例如:800 = 8 * 10 ^ 2
再看10 = 2 ^ 1 * 5 ^ 1
800 = 5 ^ 2 * 2 ^ 5
1000 = 5 ^ 3 * 2 ^ 3
即:对于任意一个末尾有K个0的数都可以转换成X * 10^K 的形式
而任意 X * 10^K 形式的数都可以转换成 5 ^ N * 2 ^ M
其中 min(N , M) == K
这样就把问题转换成从1号位置开始枚举到n号位置
找到有一个区间使得min(s2[i],s5[i]) == K
但是注意由于我们对于每一个s2 和 s5 的因子个数都继承了它上一个数的因子个数
因此在实际代码中对于查找的因子个数应该是 s[i - 1] + K;
例如: 125 8 1 1
下标 1 2 3 4
对于s5[3]而言它的因子5完全由s5[2]继承而来
这里顺便例举s2的值 s2[1] = 0 s2[2] == s2[3] == s2[3] == 3
在枚举1号位置的时候125 s5[1] == 3
第一个合法位置由s5[2]开始 此时 min(s5[2],s2[2] ) == 3
结束位置为4
第一轮得到的子序列数为 4 - 1 == 3;
但是注意到第二轮枚举时
由于s5[2]的5完全由s5[1]继承而来,所以事实上s2[2]在合法范围为[2,n]时已经没有125的支撑,
如果要使得区间[2,n]依旧实际满足存在有3个为5的因子应该要满足在去掉s5[1]的前提下依旧有3个为5的因子 即 == >> " s2[2] - s2[1] == 3 " == >> s2[2] == s2[1] + K
推出对于每一轮我们二分查找s2和s5对应的目标值p2和p5应该是s2[i - 1] + K 和 s5[i - 1] + K
== >> p2 = s2[i - 1] + K
== >> p5 = s5[i - 1] + K
其中区间长度(上界 - 下界)就为连续子段个数
但是要注意对于左边界不能小于当前枚举的位置i,因此我们用l = max(l,i)来维护枚举范围的合法性
F-Kevin的哈希构造_牛客小白月赛73 (nowcoder.com)
省流:这题不会-_-||G-MoonLight的冒泡排序难题_牛客小白月赛73 (nowcoder.com)
分析一下:对于冒泡排序,每一轮从未排序的元素中确定一个最大值将其排到未排序序列中的最后一个位置
再分析一下答案的组成
一:求出长度为n的数组的所有可能排列,以及每一个排列所需要的操作轮数
二:根据排列可能和每一个排列所需要的操作轮数求出长度为n的数组完成排序的期望操作数
三:求出期望值E = p / q;
四:根据期望值代入公式得到最终结果公式:p * q^(mod - 2) % mod;
先看一:
对于一个数是否需要满足pi != i,就是判断这个数pi是否满足它在排序前和排序后位置保持不变
如果满足说明在他后面的数都比他大或者说pi是在未排序序列中最大的值,也就是只要pi != i,那么pi就至少需要就行排序一次
对于二,三推出期望值的规律如下
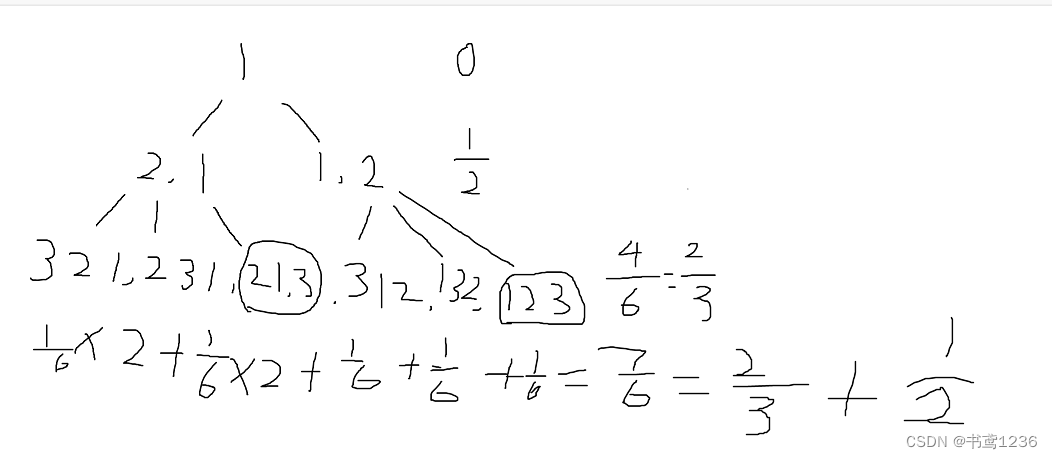
最后可以得到一个期望公式 ans(n) = 1 / 2 + 2 / 3 + …… + n - 1 / n
最后四:
根据得到的ans(n)代入公式: p * q^(mod - 2) % mod;
由于mod的值很大,常规pow求值会爆,通过快速幂求值的方式每次得到的结果 % mod后返回最终结果得到答案,
代码如下:
#include<bits/stdc++.h>
using namespace std;
using namespace std;
#define endl '\n'
#define int long long
const int mod = 998244353, maxn = 2e5 + 10;
int n, m, k, N, M, K, A, B;
vector<int>ans(maxn);
int mypow(int a, int n)
{
int ans = 1;
while (n)
{
if (n & 1)
{
n -= 1;
ans = ans * a % mod;
}
else
{
n /= 2;
a = a * a % mod;
}
}
return ans;
}
void Init()
{
for (int i = 1; i <= maxn; i++)
ans[i] = (ans[i - 1] + (i - 1) * mypow(i, mod - 2) ) % mod;
}
void solve()
{
cin >> n;
cout << ans[n] << endl;
}
signed main()
{
cin.tie(0)->sync_with_stdio(false);
Init();
int t;
cin >> t;
while (t--)
solve();
return 0;
}