🚀位图

学习位图前，我们先来看一道题
在这里插入图片描述

用哈希表存储每个整数？不行，数量太大了，存储不下这么多数据。
对这些整数先排序，在用二分查找？也不行，同理，数据量太大了，不好存储数据，排序都能成问题，更何况来查找。
遍历一遍。当然这个是可以的，但是题目是快速，所以时间还是慢了。

好的，这里就慢慢引出今天的主角，位图。

💡概念

位图是一种数据结构，用于表示一个二进制数组中的位或标记

位图通常是一个非常紧凑的数据结构，可以通过一个位来表示一个存储单元。例如，如果一个位图有8个位，那么可以用一个字节表示它们，如果有32个位，那么可以用一个4字节的数据表示它们。

位图的特点是可以高效地进行位运算，例如按位与、按位或、按位取反、按位移动等。因为这些运算都只需要单个 CPU 周期，所以位图非常适合于高性能计算和大型数据集合的处理。

💡接口操作

C++中是有位图的库，我们只需要包头文件 #include< bitset > 即可使用在这里插入图片描述

这里先简单认识一下常用的bitset的接口函数
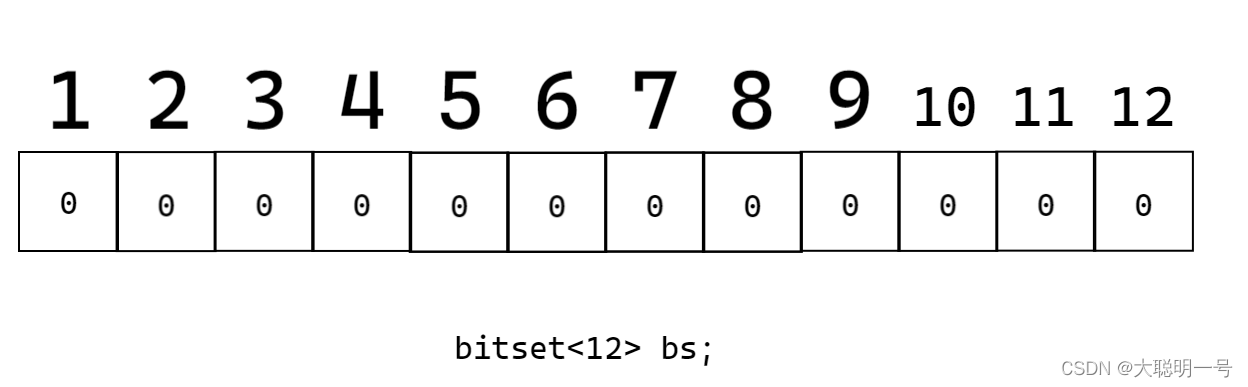
在这里插入图片描述

set(n) -------- 将第n个比特位设置为1
reset(n) ----- 将第n个比特位设置为0
test(n) ------- 检查第n个比特位，是1返回真，0返回假

那么我们回到题目
用位图来存储每个数字的状态，0表示不在，1表示在，每个比特位表示一个数字，就是有40亿个数（约等于2³²bit ≈ 4GB大小）也可以装得下，而且查找的时间复杂度是O(1)，快的起飞。

🚀布隆过滤器

💡思想

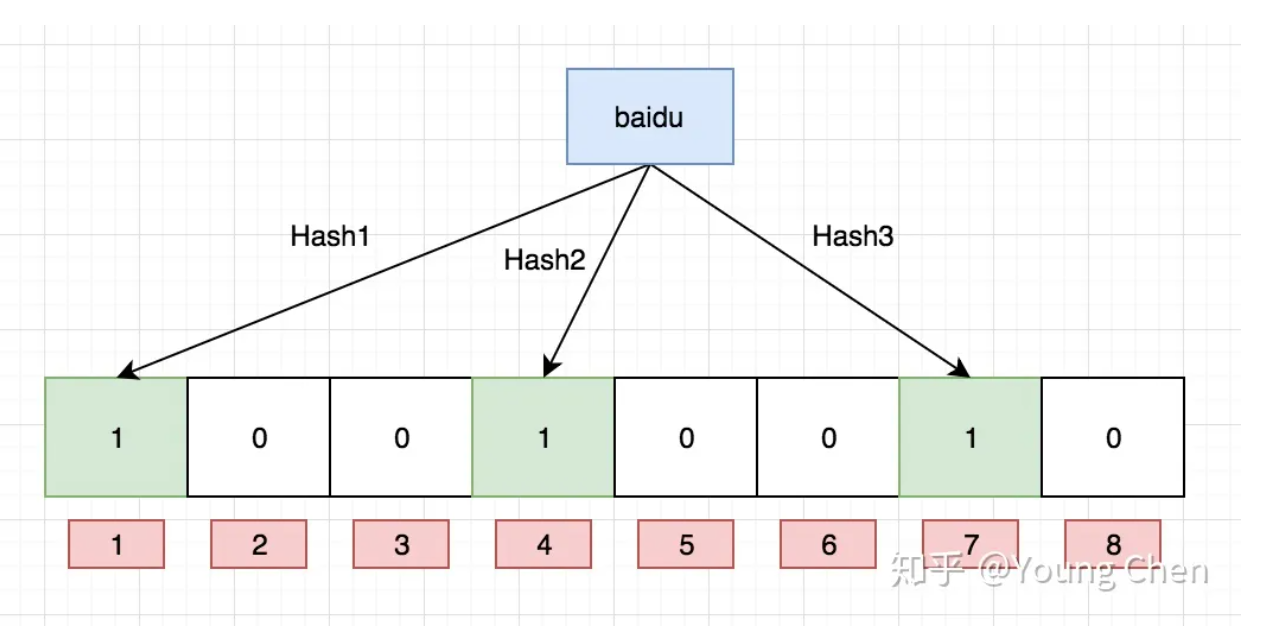
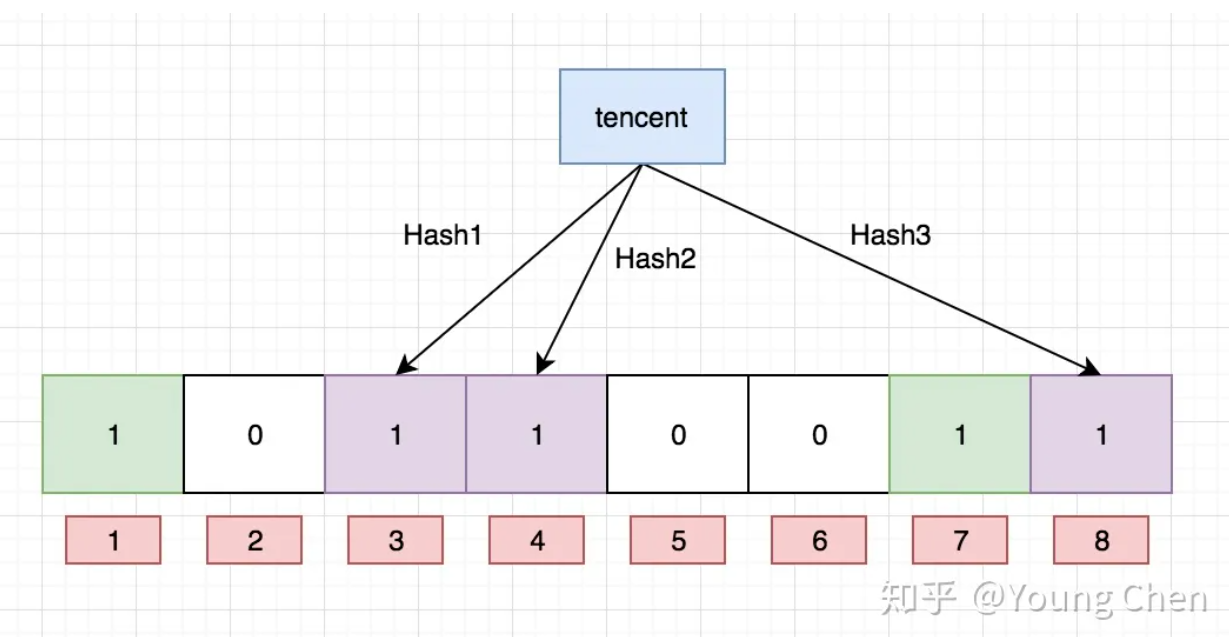
我们知道哈希表是调用一次哈希函数映射到表里的，而布隆过滤器也是这个思想，只不过是多次进行哈希映射，且映射到位图里。

图片转载

假设 jingdong 映射的是 1 2 3上的比特位，我们在查询的时候发现2号为0，这时候我们可以肯定 jingdong 这个值一定不存在，而我们查询baidu，发现 1 4 7上的比特位都为1，这个时候我们能认为baidu就一定存在吗？答案是否定的，只是可能存在。因为不排除其他值的组合恰好凑成了 1 4 7上的比特位为1。
布隆过滤器的删除
布隆过滤器一般是不建议删除的，就算用计数，也会影响到其他值的存在，因为删除操作会增加误判率，所以一般是不建议删除的，如果需要可以根据具体使用场景来实现支持删除的布隆过滤器。

💡实现代码

struct BKDRHash
{
	size_t operator()(const string& s)
	{
		// BKDR
		size_t value = 0;
		for (auto ch : s)
		{
			value *= 31;
			value += ch;
		}
		return value;
	}
};
struct APHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 0;
		for (long i = 0; i < s.size(); i++)
		{
			if ((i & 1) == 0)
			{
				hash ^= ((hash << 7) ^ s[i] ^ (hash >> 3));
			}
			else
			{
				hash ^= (~((hash << 11) ^ s[i] ^ (hash >> 5)));
			}
		}
		return hash;
	}
};
struct DJBHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 5381;
		for (auto ch : s)
		{
			hash += (hash << 5) + ch;
		}
		return hash;
	}
};
struct JSHash
{
	size_t operator()(const string& s)
	{
		size_t hash = 1315423911;
		for (auto ch : s)
		{
			hash ^= ((hash << 5) + ch + (hash >> 2));
		}
		return hash;
	}
};
template<size_t N,
	class K = string,
	class HashFunc1 = BKDRHash,
	class HashFunc2 = APHash,
	class HashFunc3 = DJBHash,
	class HashFunc4 = JSHash>
class bloomfilter
{
private:
	bitset<N> _bs;
public:
	void set(const K& key)
	{
		size_t n1 = HashFunc1()(key) % N;
		size_t n2 = HashFunc2()(key) % N;
		size_t n3 = HashFunc3()(key) % N;
		size_t n4 = HashFunc4()(key) % N;

		_bs.set(n1);
		_bs.set(n2);
		_bs.set(n3);
		_bs.set(n4);
	}
	bool test(const K& key)
	{
		size_t n1 = HashFunc1()(key) % N;
		size_t n2 = HashFunc2()(key) % N;
		size_t n3 = HashFunc3()(key) % N;
		size_t n4 = HashFunc4()(key) % N;

		if (_bs.test(n1) && _bs.test(n2) && _bs.test(n3) && _bs.test(n4))
			return true;
		return false;
	}

	// 一般不实现，因为BloomFilter采用多重哈希映射，就决定了还原的时候必然会影响到其他值
	bool reset(const K& key);
};

💡实际应用

布隆过滤器常用于需要快速判断某个元素是否存在于一个集合中的场景，尤其适用于数据量庞大、查询频繁的情况。以下是一些具体的实际应用：

网络爬虫优化：网络爬虫需要快速判断一个网页是否已经爬取过，以避免重复爬取。使用布隆过滤器可以快速判断一个网页是否已经爬取过，避免重复爬取。

垃圾邮件过滤：垃圾邮件过滤需要快速判断一封邮件是否是垃圾邮件。使用布隆过滤器可以将一些常见的垃圾邮件关键词或者特征加入到集合中，用于快速判断待过滤的邮件是否属于垃圾邮件。

搜索引擎索引优化：在搜索引擎索引过程中，需要快速判断一个单词是否出现在某个网页中。使用布隆过滤器可以将某个单词的哈希值加入到集合中，用于快速判断该单词是否出现在某个网页中。

大规模缓存数据的快速查询：在缓存数据中，如果需要快速判断某个键是否存在于缓存中，可以使用布隆过滤器来实现快速查询。

总的来说，布隆过滤器在需要快速判断某个元素是否在一个集合中时具有广泛的应用价值，特别是在数据量庞大、查询频繁的场景下，其效果更为明显。