目录
1. 二叉搜索树（BST）
1.1 二叉搜索树概念
1.2 二叉搜索树操作
1.2.1 二叉搜索树的查找
1.2.2 二叉搜索树的插入
1.2.3 二叉搜索树的删除
2. 二叉搜索树的实现
2.1BST基本结构
2.2 BST操作成员函数(非递归）
2.3 BST操作成员函数（递归）
3. 二叉搜索树的应用
4. 二叉搜索树的性能分析
1. 二叉搜索树（BST）
1.1 二叉搜索树概念
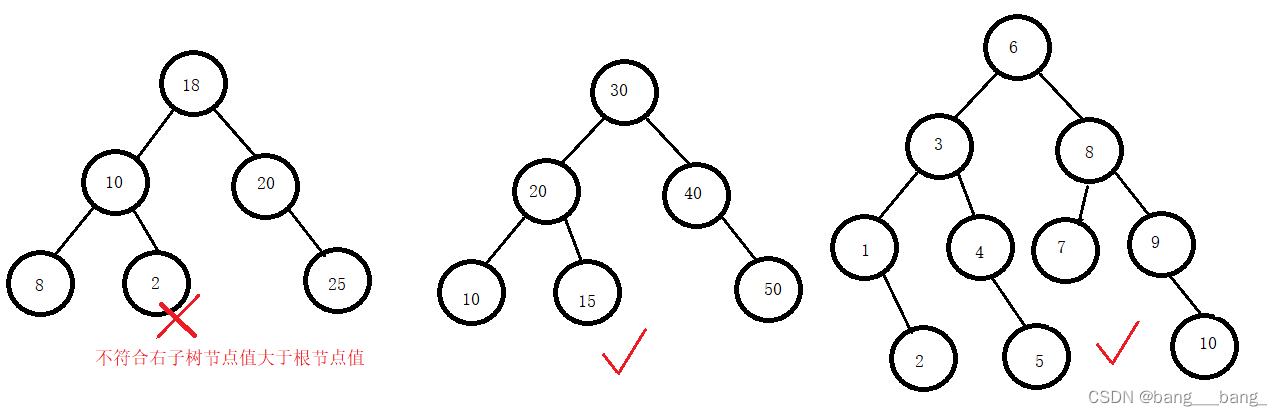
二叉搜索树又称二叉排序树，它或者是一棵空树，或者是具有以下性质的二叉树：
- 若它的左子树不为空，则左子树上所有节点的值都小于根节点的值
- 若它的右子树不为空，则右子树上所有节点的值都大于根节点的值
- 它的左右子树也分别为二叉搜索树
我举几个例子，更直观的看清楚结构：
1.2 二叉搜索树操作
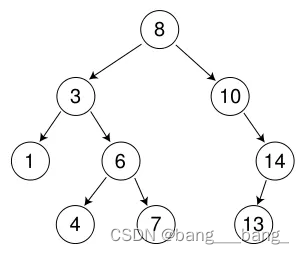
int a[] = {8, 3, 1, 10, 6, 4, 7, 14, 13};1.2.1 二叉搜索树的查找
- 从根开始比较，查找，比根大则往右边走查找，比根小则往左边走查找。
- 最多查找高度次，走到空，还没找到，则这个值不存在。
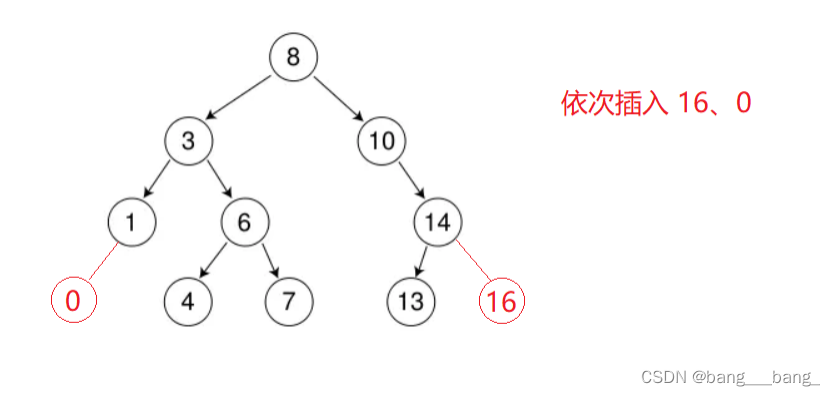
1.2.2 二叉搜索树的插入
插入的具体过程如下：
- 树为空，则直接新增节点，赋值给root指针
- 树不为空，按二叉搜索树性质查找插入的位置，插入新节点（记录父节点，判断插入的节点应该在父节点的左子树还是右子树）
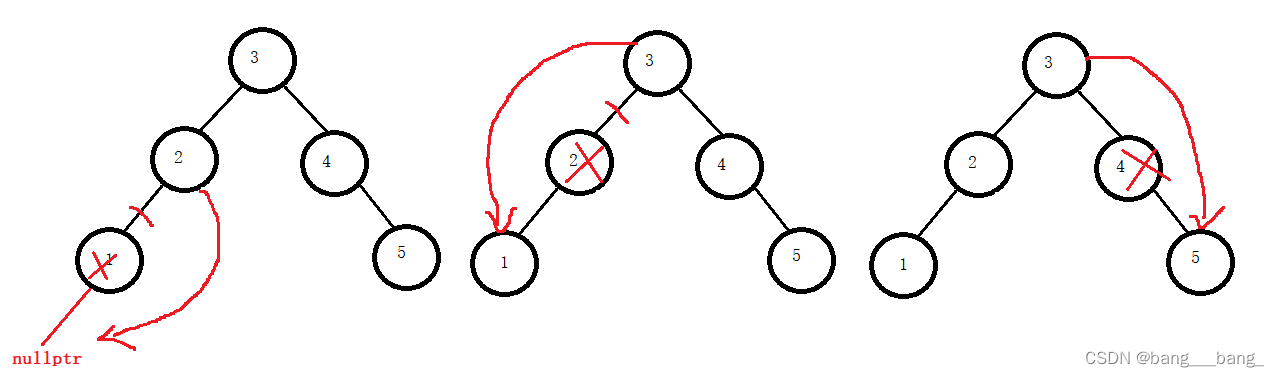
1.2.3 二叉搜索树的删除
首先查找元素是否在二叉搜索树中，如果不存在，则返回, 否则要删除的结点可能分下面四种情
况：
a. 要删除的结点无孩子结点
b. 要删除的结点只有左孩子结点
c. 要删除的结点只有右孩子结点
d. 要删除的结点有左、右孩子结点
看似删除节点有4种情况，但实际上a和b和c可以合并，这样就只有2种情况了：
a:待删除的结点无孩子/只有一个孩子：删除结点并使父亲结点指向被删除结点的孩子结点（无孩子视为孩子是空结点，任意指向一个即可）
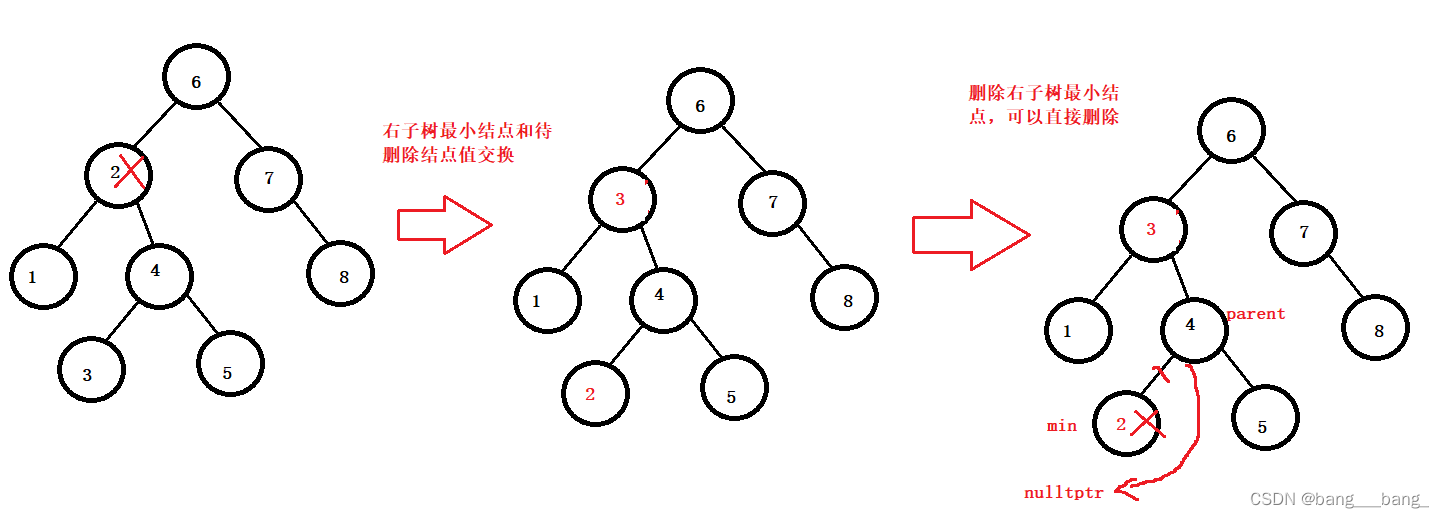
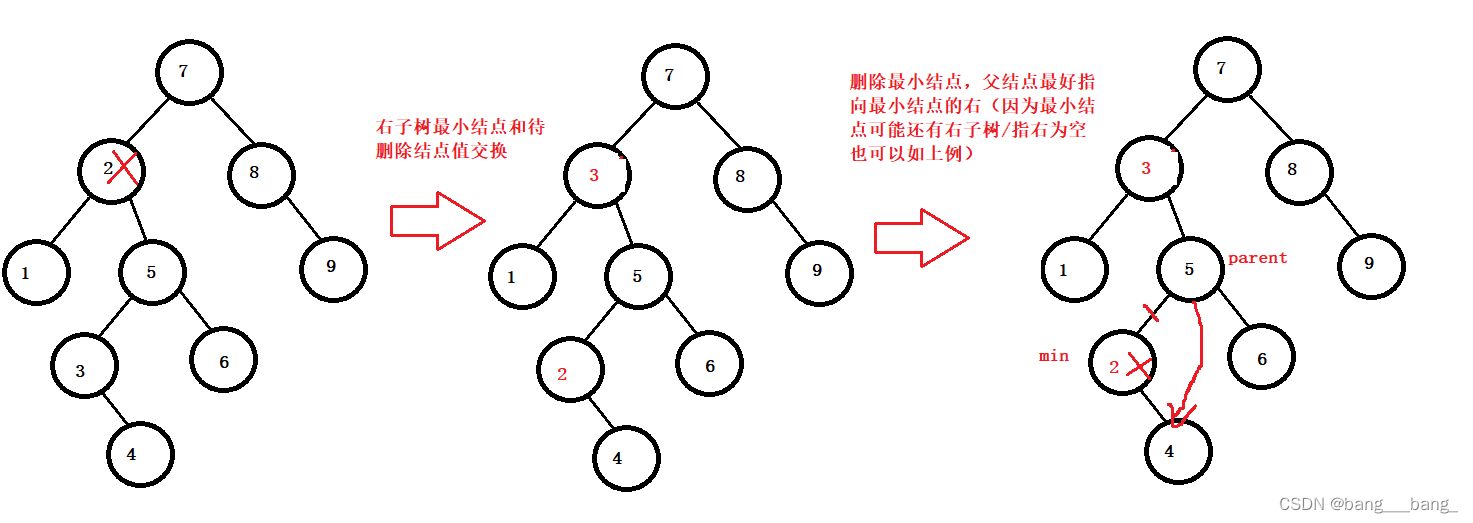
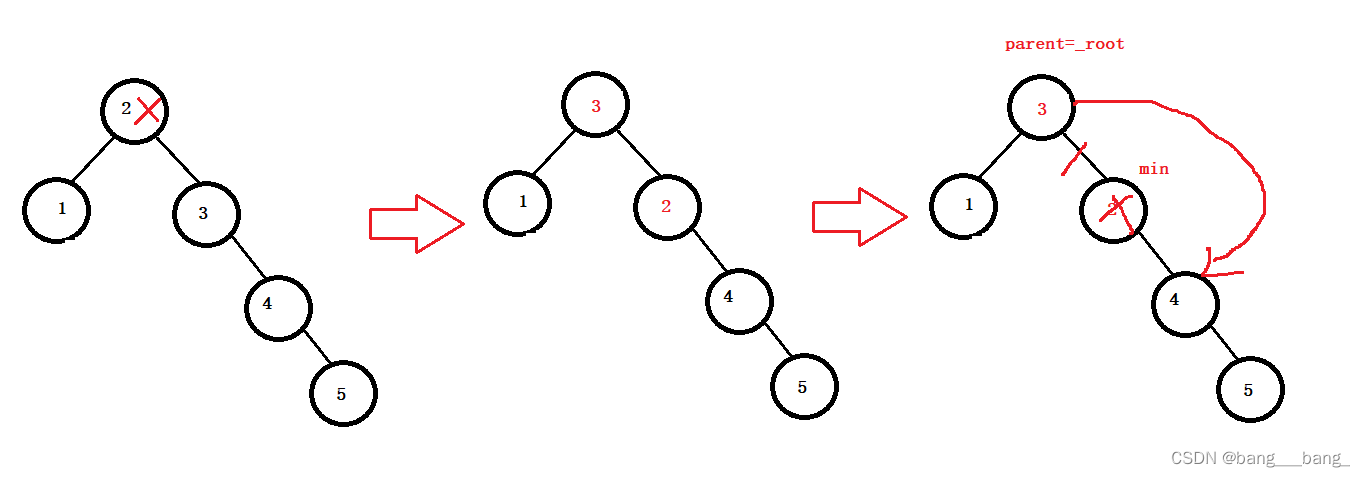
b:待删除的结点有左右孩子：采用替换法，寻找删除结点右子树的最小结点（右子树最左结点），将最小结点的值和删除结点的值替换，然后删除最小结点（此时最小结点，要么没有孩子，要么只有一个孩子，符合a情况可以直接删除）
2. 二叉搜索树的实现
2.1BST基本结构
结点：
template<class K>
struct BSTreeNode
{
BSTreeNode<K>* _left;
BSTreeNode<K>* _right;
K _key;
BSTreeNode(const K& key)
:_left(nullptr)
, _right(nullptr)
, _key(key)
{}
};BST树：
template<class K>
class BSTree
{
typedef BSTreeNode<K> Node;
public:
//成员函数
private:
Node* _root=nullptr;
};查找：
bool Find(const K& key)
{
Node* cur = _root;
while (cur)
{
//待查值大于当前结点，去右子树
if (cur->_key < key)
{
cur = cur->_right;
}
//待查值小于当前结点，去左子树
else if (cur->_key > key)
{
cur = cur->_left;
}
//找到
else
{
return true;
}
}
return false;
}2.2 BST操作成员函数(非递归）
插入：
bool Insert(const K& key)
{
//树为空，则直接新增结点，赋值给_root指针
if (_root == nullptr)
{
_root = new Node(key);
return true;
}
Node* parent = nullptr;
Node* cur = _root;
//按性质查找插入的位置，并且记录父结点
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
//已有结点，不需要再插入
else
{
return false;
}
}
cur = new Node(key);
//判断是插入父结点的左部还是右部
if (parent->_key < key)
{
parent->_right = cur;
}
else
{
parent->_left = cur;
}
return true;
}删除：
bool Erase(const K& key)
{
Node* parent = nullptr;
Node* cur = _root;
//查找是否有待删除的节点
while (cur)
{
if (cur->_key < key)
{
parent = cur;
cur = cur->_right;
}
else if (cur->_key > key)
{
parent = cur;
cur = cur->_left;
}
else
{
// 开始删除
// 1、左为空
// 2、右为空
// 3、左右都不为空
if (cur->_left == nullptr)
{
//判断下当前节点是否是_root，若是,无法用parent(当前为nullptr，防止野指针错误)
if (cur == _root)
{
_root = cur->_right;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_right;
}
else
{
parent->_right = cur->_right;
}
}
delete cur;
cur = nullptr;
}
else if (cur->_right == nullptr)
{
if (_root == cur)
{
_root = cur->_left;
}
else
{
if (cur == parent->_left)
{
parent->_left = cur->_left;
}
else
{
parent->_right = cur->_left;
}
}
delete cur;
cur = nullptr;
}
else
{
//记录删除节点父节点
Node* minParent = cur;
//找到右子树最小节点进行替换
Node* min = cur->_right;
while (min->_left)
{
minParent = min;
min = min->_left;
}
swap(cur->_key, min->_key);
//min在父的左孩子上
if (minParent->_left == min)
//万一最左节点还有右孩子节点，或者是叶子也直接指右为空
minParent->_left = min->_right;
//min在父的右孩子上（待删除节点在根节点，最左节点为根节点的右孩子）
else
minParent->_right = min->_right;
delete min;
min == nullptr;
}
return true;
}
}
return false;
}其他成员函数这里就不展示了，这里再说一个小tips:
default：强制编译器生成默认的构造——C++11的用法
BSTree()=default;2.3 BST操作成员函数（递归）
还是递归香，看懂了上面的非递归那么就可以改造成递归了。
查找：
bool _FindR(Node*& root, const K& key)
{
if (root == nullptr)
return false;
if (root->_key < key)
{
return _FindR(root->_right, key);
}
else if (root->_key > key)
{
return _FindR(root->_left, key);
}
else
{
return true;
}
}插入：
bool _InsertR(Node*& root, const K& key)
{
if (root == nullptr)
{
root = new Node(key);
return true;
}
if (root->_key < key)
return _InsertR(root->_right, key);
else if (root->_key > key)
return _InsertR(root->_left, key);
else
return false;
}删除：
bool _EraseR(Node* root, const K& key)
{
Node* del = root;
if (root == nullptr)
return false;
if (root->_key < key)
return _EraseR(root->_right, key);
else if (root->_key > key)
return _EraseR(root->_left, key);
else
{
if (root->_left == nullptr)
root = root->_right;
else if (root->_right == nullptr)
root = root->_left;
else
{
//找右数的最左节点替换删除
Node* min = root->_right;
while (min->_left)
{
min = min->_left;
}
swap(root->_key, min->_key);
//交换后结构改变不是搜索二叉树了，规定范围在右树（因为是右树最左节点替换）再递归
return _EraseR(root->_right, key);
}
delete del;
return true;
}
}3. 二叉搜索树的应用
1. K模型 ：K模型即只有key作为关键码，结构中只需要存储Key即可，关键码即为需要搜索到的值。
比如：给一个单词word，判断该单词是否拼写正确，具体方式如下：
以词库中所有单词集合中的每个单词作为key，构建一棵二叉搜索树
在二叉搜索树中检索该单词是否存在，存在则拼写正确，不存在则拼写错误。
2. KV模型 ：每一个关键码key，都有与之对应的值Value，即<Key, Value>的键值对。该种方式在现实生活中非常常见：
比如英汉词典就是英文与中文的对应关系，通过英文可以快速找到与其对应的中文，英文单词与其对应的中文<word, chinese>就构成一种键值对；
再比如统计单词次数，统计成功后，给定单词就可快速找到其出现的次数，单词与其出
现次数就是<word, count>就构成一种键值对。
4. 二叉搜索树的性能分析
插入和删除操作都必须先查找，查找效率代表了二叉搜索树中各个操作的性能。
对有n个结点的二叉搜索树，若每个元素查找的概率相等，则二叉搜索树平均查找长度是结点在二叉搜索树的深度的函数，即结点越深，则比较次数越多。
但对于同一个关键码集合，如果各关键码插入的次序不同，可能得到不同结构的二叉搜索树：
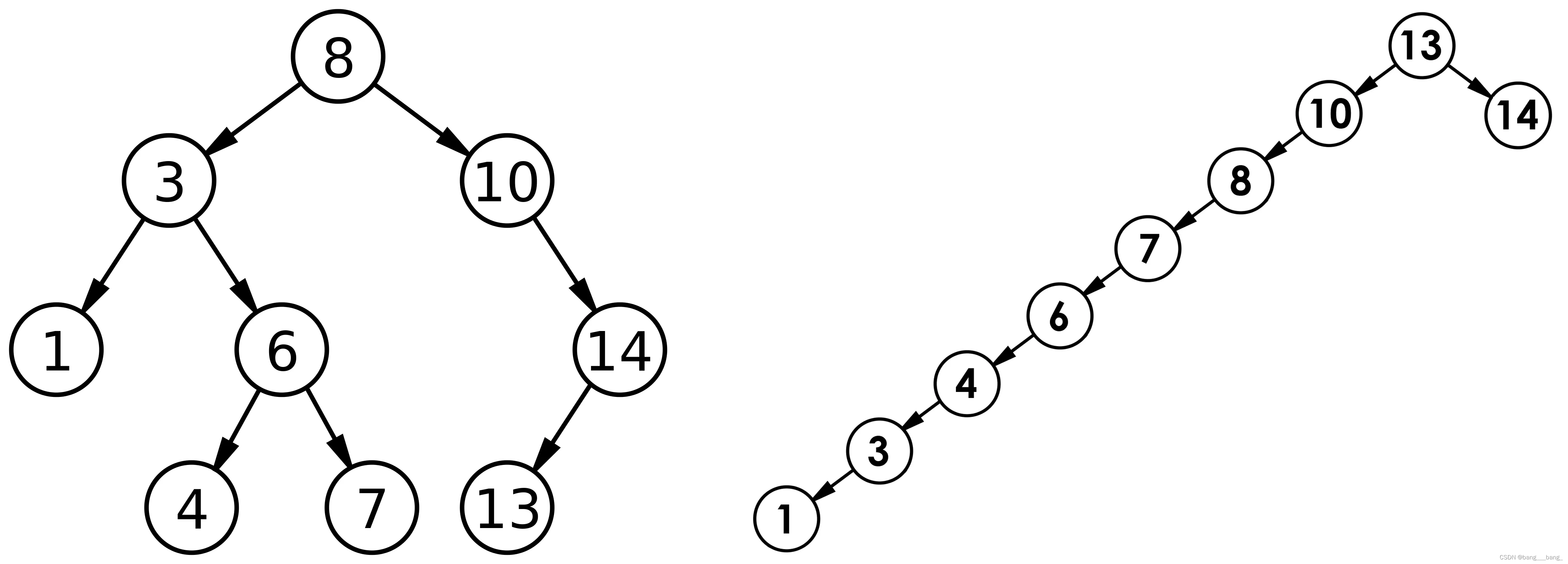
最优情况下：二叉搜索树为完全二叉树（或者接近完全二叉树），其平均比较次数为：log(N)
最差情况下：二叉搜索树退化为单支树（或者类似单支），其平均比较次数为 N
如果退化为单支树，二叉搜索树的性能就失去了。那能否进行改进？无论按照什么次序插入关键码，都能达到最优？这就需要AVL树和红黑树了。
