1. 作者介绍

梁有成，男，西安工程大学电子信息学院，2022级研究生
研究方向：三维点云处理
电子邮件：401138472@qq.com

路治东，男，西安工程大学电子信息学院，2022级研究生
研究方向：机器视觉与人工智能
电子邮件：206307079527@qq.com

2. 朴素贝叶斯算法简介及案例

2.1朴素贝叶斯算法简介

朴素贝叶斯算法（Naive Bayes）是一种基于概率论和贝叶斯算法来预测文本的分类（如新闻或客户评论）的概率算法。贝叶斯算法将文本概率化——这种算法计算给定文本为每种分类的概率，然后输出具有最高概率值的分类。

抽象一些的说，朴素贝叶斯分类器会单独考量每一维度特征被分类的条件概率，进而综合这些概率并对其所在的特征向量做出分类预测。因此，这个模型的基本数学假设是：各个维度上的特征被分类的条件概率之间是相互独立的。朴素贝叶斯模型有着广泛的实际应用环境，特别是在文本分类的任务中，包括互联网新闻的分类，垃圾邮件的筛选等。

朴素贝叶斯思想基础：对于待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。通俗地讲，好比你在街上看到一个黑人，我问你他是从哪里来的，你十有八九会说从非洲。为什么呢？因为黑人中非洲人比例最高，当然别人也有可能是美洲人或者拉丁人，但在没有其他可用信息下，我们会选择条件概率最大类别，这就是朴素贝叶斯思想基础。

贝叶斯分类的定义：
1.设x={a1, a2, …,am}为一个待分类项，而每个a为x的一个特征属性；
2.有类别集合C = {y1,y2, …, yn}
3.计算P(y1|x), P(y2|x),…, P(yn|x)
4.如果P(yk|x)= max{ P(y1|x), P(y2|x), …, P(yn|x) }，则x∈yk.

关键是如何计算第3步中的各个条件概率。步骤：
1.找到一个已知分类的待分类项集合，这个集合叫做训练样本集。
2.统计得到在各类别下各个特征属性的条件概率估计。即：
在这里插入图片描述
3.如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

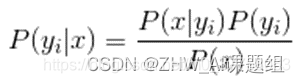
因为分母对于所有类别为常数，只要将分子最大化即可。又因为各特征属性是条件独立的，所以有：

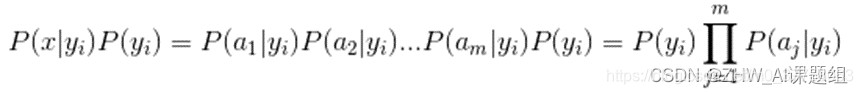
朴素贝叶斯流程：

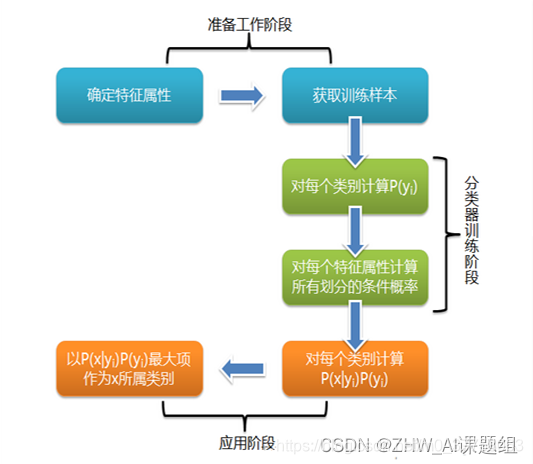
可以看到，整个朴素贝叶斯分类分为三个阶段：

第一阶段——准备工作阶段，这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人工对一部分待分类项进行分类，形成训练样本集合。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量对整个过程将有重要影响，分类器的质量很大程度上由特征属性、特征属性划分及训练样本质量决定。

第二阶段——分类器训练阶段，这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并将结果记录。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

第三阶段——应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

2.2文本分类器

下面通过这个例子来简要介绍朴素贝叶斯算法：
假设我们正在构建一个分类器，该分类器将会判断文本是否与体育有关。我们的训练数据有以下5句话：
在这里插入图片描述
text为文本，tag为文本的类别，这里简单的分为运动类和非运动类
我们将根据这五句话的分类，来判断“A very close game”这个句子应该被分为哪一个类别。

作为一个概率分类器，我们要计算“A very close game”一句属于体育（Sports）类别的概率，以及它不是体育（Not sports）的概率。计算完毕后，我们将会把他分类到概率值更大的一类中。

计算主要步骤
（1）创建你的特征——数字化你的要素
要利用一个公式进行数学计算，我们首先需要的就是数字，但是对于一个文本来讲，我们并没有直接的要素可以得到，所以我们首先要创建一个可以由数字表达同时可以体现出文本信息的特征。

对于英文来说，数字化文本信息最简单的一种方法就是计算一段文本中各个词语的词频。也就是说，我们可以简单地忽略掉单词的顺序和句子的结构，将每段文本粗暴地看做一组单词的集合。于是我们提炼的特征将是每个单词出现的次数。这种方法看起来非常简单粗暴，然而效果却出奇的好。

（2）由贝叶斯定理得到概率公式
事实上，在我们的数据中，我们没有办法直接得到P(sports|“A very close game”)，但是贝叶斯定律提供了一种计算条件概率的方法：
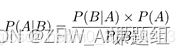
在这里插入图片描述
所以根据这个公式，我们可以把我们的P(sports|“A very close game”)转化为：

由于sports和notsports的计算式中的分母相同，因此我们在比较时可以舍弃除数，然后直接进行比较，即：

这两个式子中的概率我们都可以直接根据我们的数据得到，如P（a very close game|Sports）只需计算“A very close game”一句出现在“Sport”分类中的次数，再除以总数即可，P（Sports）只需计算sports类型的文本除以文本的总数即可。至此，我们所需的数据就全部得到了。

不过仍然存在一个问题：我们的训练数据中没有出现“A very close game”，因此直接计算的话，我们计算出的概率将为零。除非我们要分类的每个句子都出现在我们的训练数据中，否则该模型将不会非常有效，我们需要一个泛用性更加强大的模型。

（3）将模型朴素化
于是，朴素化的模型应运而生：我们假定句子中的每个单词都独立于其他单词。这意味着我们不再查看整个句子，而是查看单个单词。

根据前文思想，我们可以写出这个公式：
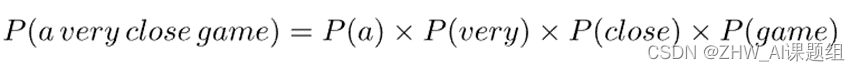
在这里插入图片描述
事实上，这个假设确实十分有效，同时使得朴素贝叶斯模型能够很好地处理少量数据与可能分类错误的数据。接下来就是将其应用于我们之前的工作：

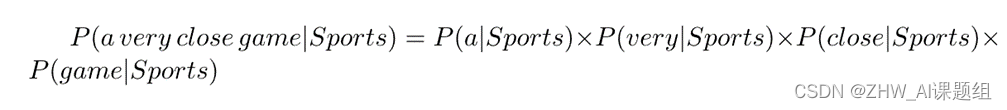
这样一来，所有的单词实际上都在我们的训练数据中出现了几次，于是我们便可以计算出概率来了。

（4）计算最终概率
至此，我们只需要计算每种分类（Sports与not sports）的概率，然后看看哪个概率更大。

我仅仅取用了训练数据中的数据来进行计算。

首先，我们计算每个类别的先验概率：对于我们训练数据中的给定句子，其为Sports
P（Sports）的概率为3/5。而P(Not sports）为2/5。

然后，计算，即计算“game”一词在Sports的文本中出现的次数（2次）除以Sports文本中的单词总数（11次）。因此，可以得到：
在这里插入图片描述
这样下去我们又会遇到一个问题：“close”没有出现在任何Sports文本中。这样计算的话该概率将是0。而我们最终的式子需要几个概率相乘：

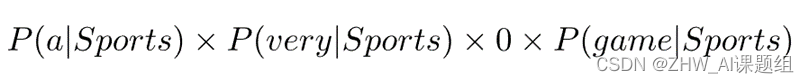
这样的话我们之前的努力就会因为一个不曾出现的单词而白费。

不过拉普拉斯平滑法（Laplace smoothing）可以很好的解决这个问题：即我们为每个计数加1，这样一来他们永远不会为零。为了平衡这一点，我们将可能的单词的数目添加到除数中去（训练样本中出现的单词数。请注意：如果某个特定单词在训练样本中出现多次，则该单词的数目将被计为1次）。因此除法的值永远不会大于1。
在我们的数据中，可能的词是：
[‘a’，‘great’，‘very’，‘over’，‘it’，‘but’，‘game’，‘election’，‘clean’，‘close’，‘the’，‘was’，'forgetable‘，“match”]。

由于所有可能的单词数是14，因此应用平滑处理可以得出：
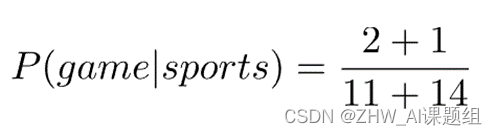
在这里插入图片描述
最终得到的结果是：

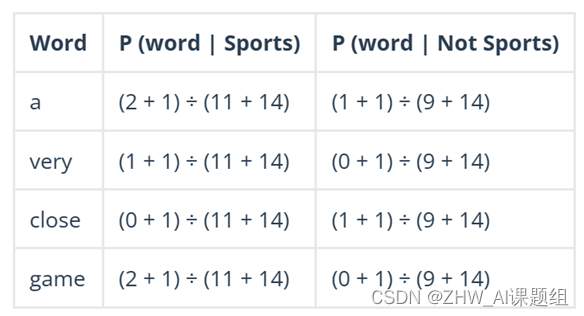
这样就只剩最后一步了，现在我们将所有概率计算出来，看看哪个个概率更大：

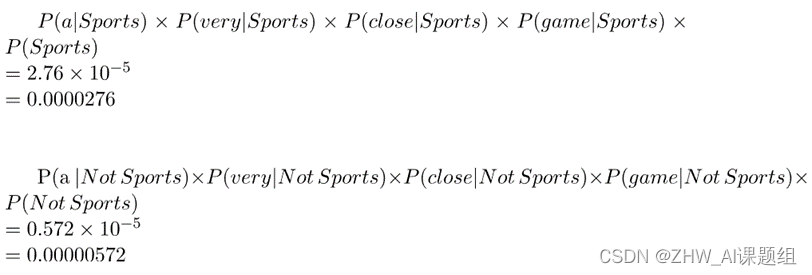
可以看到，0.0000276>0.00000572,故而我们的分类器将文本"A very close game"分类为与Sports相关的文本了。

2.3对新闻文本进行文本分类

文本特征向量化

使用朴素贝叶斯模型去给文本数据分类，就必须对文本数据进行文本特征向量化
本节课使用CountVectorizer进行文本特征向量化
CountVectorizer会统计特定文档中单词出现的次数（统计词频）
CountVectorizer通过fit_transform()函数计算各个词语出现的次数

加载新闻数据、文本分类
本案例使用sklearn.datasets.fetch_20newsgroups函数下载新闻数据（比较耗时）
使用sklearn.naive_bayes.MultinomialNB进行文本分类

问题引出
本文使用Scikit-learn中集成的经典的20类新闻文本作为实验数据。
需要提醒的是，本文中的数据没有预存，需要实时从网上下载，而在墙内下载速度有点慢，因此建议翻墙下载。
下面我们先看下数据：
from sklearn import datasets
news = datasets.fetch_20newsgroups(subset=‘all’)
print(len(news.data)) #news.data的数据格式为list
print(news.data[0])
在这里插入图片描述
从图中我们可以看到，我们的原始数据包含是18846条文本的列表，共有20个类别。由于原始数据中既没有被设定特征，也没有数字化量度。因此在交给朴素贝叶斯分类器学习之前，要对数据进行进一步的处理。

3. Python 代码实现

3.1文本分类器

1.源码

'''计算单词在tag类中出现的次数'''
def countWord(word,tag):
    count = 0
    for sentence in tag:
        for w in sentence.split():
            if(word == w):
                count = count + 1
    print(word,":  ",count)
    return count

'''计算文本str属于tag类的朴素贝叶斯概率'''
def caculateNBP(str,tag,Ptag,All,tagNum):
    str = str.lower()
    words = str.split(" ")
    pList = []
    for word in words:
        P = (1+countWord(word,tag))/(All + tagNum)
        pList.append(P)
    NBP = 1
    print(pList)
    for P in pList:
        NBP = NBP * P
    NBP = NBP*Ptag
    return NBP
'''训练数据'''
texts = ["A great game", "The election was over", "Very clean match", "A clean but forgettable game", "It was a close election"]
Sports = ["A great game", "Very clean match", "A clean but forgettable game"]
NotSports = ["The election was over", "It was a close election"]
'''转小写'''
texts2 = [s.lower() for s in texts if isinstance(s,str)==True]
Sports2 = [s.lower() for s in Sports if isinstance(s,str)==True]
NotSports2 = [s.lower() for s in NotSports if isinstance(s,str)==True]
'''计算P(Sports)和P(NOT SPORTS)'''
Psports = len(Sports)/len(texts)
PnotSports = len(NotSports)/len(texts)
str = "100"
allWords = []#所有可能的单词
for sentence in texts2:
    temp = sentence.split(" ")
    allWords = allWords + temp
allWords = set(allWords)
allWords = list(allWords)
lenAllWords = len(allWords)#所有可能的单词数量

numofSports = 0#Sports类文本的单词数
for sentence in Sports2:
    temp = len(sentence.split())
    numofSports = numofSports + temp

numofNotSports = 0#notSports类文本的单词数
for sentence in NotSports2:
    temp = len(sentence.split())
    numofNotSports = numofNotSports + temp

str = "A very close game"
print("计算sports概率：---------------------------------------------")
pSports = caculateNBP(str,Sports2,Psports,numofSports,lenAllWords)
print("P(STR|SPORTS)= ",pSports)
print("计算not sports概率：---------------------------------------------")
pNotSports = caculateNBP(str,NotSports2,PnotSports,numofNotSports,lenAllWords)
print("P(STR|NOTSPORTS)= ", pNotSports)
print("分类结果：   ")
if(pSports > pNotSports):
    print("文本  ",str,"  可以被分为Sports类")
else:
    print("文本  ",str,"  可以被分为Not Sports类")

2.运行结果
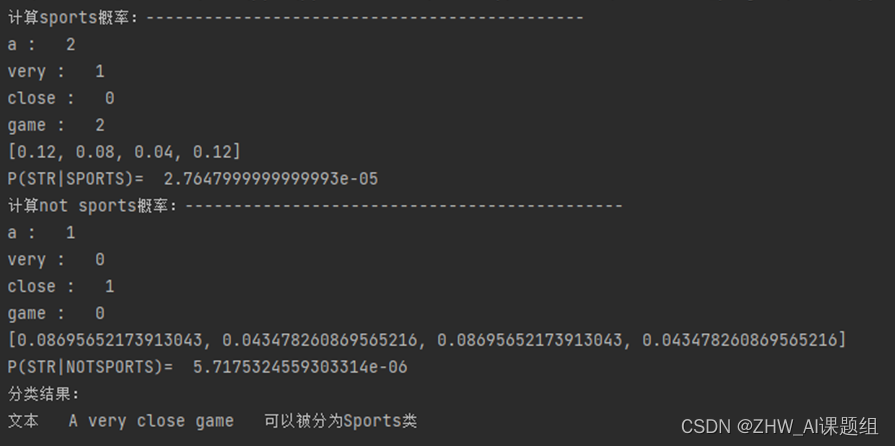
在这里插入图片描述

3.2 新闻文本分类

1.源码

from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import classification_report

#获取数据
news = datasets.fetch_20newsgroups(subset='all')

#将数据拆分为训练集和测试集
X_train, X_test, y_train, y_test = train_test_split(news.data, news.target, 
													test_size=0.25, random_state=33)

#导入文本特征向量转化模块，并将文本特征向量化
vec = CountVectorizer()
X_train = vec.fit_transform(X_train)
X_test = vec.transform(X_test)    #注意这个函数与上面的不一样

#使用默认配置初始化朴素贝叶斯模型
mnb = MultinomialNB()
#利用训练数据对模型参数进行估计，并进行预测
mnb.fit(X_train, y_train)
y_predict = mnb.predict(X_test)

#输出预测结果
print('The Accuracy of Naive Bayes:', mnb.score(X_test, y_test))
print(classification_report(y_test, y_predict, target_names=news.target_names))

2.运行结果
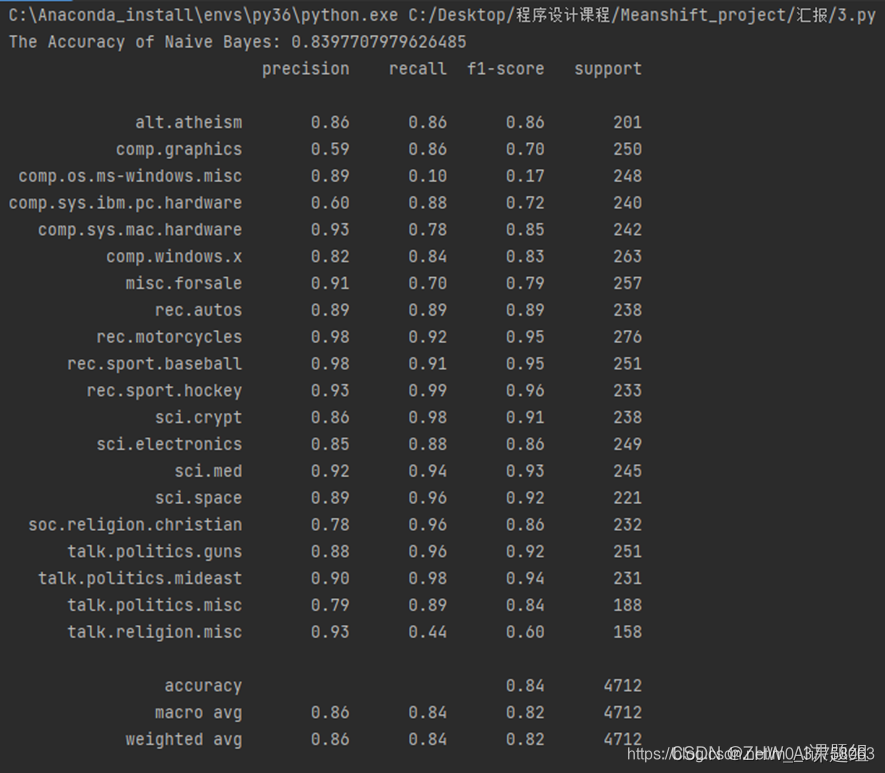
在这里插入图片描述
上图的结果可以看出，朴素贝叶斯对4712个测试样本分类准确性约83.977%，结果还是比较不错的。

小结：
1.朴素贝叶斯被广泛运用于海量互联网文本分类任务。
2.由于其较强的特征条件独立假设，使得模型预测所需要估计的参数规模从幂指数量级到线性量级减少，极大的节约了内存消耗和计算时间。
3.受这种强假设的限制，模型训练时无法将各个特征之间的联系考量在内，使该模型在特征之间关联性较强的分类任务上性能表现不佳。

参考（可供参考的链接和引用文献）

1.[简单的朴素贝叶斯算法实现英文文本分类（Python实现,把关于sport和not sport的分类,用上次实验代码走一遍。走的流程包括:1.创_Akira_oono的博客-CSDN博客]https://blog.csdn.net/weixin_44405843/article/details/109365790
2.[sk-learn实例-用朴素贝叶斯算法（Naive Bayes）对文本进行分类_张大千09的博客-CSDN博客]
https://monkeylearn.com/blog/practical-explanation-naive-bayes-classifier/