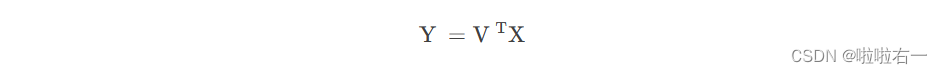本文整理自
- 长路漫漫2021的原创博客:sklearn基础篇(九)-- 主成分分析(PCA)
- 李春春_的原创博客:主成分分析(PCA)原理详解
- bilibili视频:用最直观的方式告诉你:什么是主成分分析PCA
文章目录
- 📚降维
- 📚 PCA的思想
- 📚用最直观的方式告诉你:什么是主成分分析PCA😄
- 🐇PCA是什么?
- 🐇怎么找坐标系,特别是怎么找方差最大的方向?
- 🐇怎么求R?协方差矩阵的特征向量就是R!
- 🥕协方差
- 🥕协方差矩阵
- 🥕协方差矩阵的特征向量
- 🐇总结一下PCA怎么求解?
- 🐇PCA和奇异值分解
- 📚PCA的推导:基于最小投影距离
- 📚PCA的推导:基于最大投影方差
- 📚PCA算法流程⭐️
- 🐇特征值分解算法
- 🥕观测数据规范化处理,得到规范化数据矩阵X
- 🥕计算相关矩阵R
- 🥕求R的特征值和特征向量
- 🥕求k个样本主成分
- 🥕计算k个主成分yi与原变量xi的相关系数ρ(xi,yi)以及k个主成分对原变量xi的贡献率vi
- 🥕计算n个样本的k个主成分值
- 🐇PCA实例
- 🐇奇异值分解算法
- 🥕构造新的n×m矩阵
- 🥕对矩阵X′进行截断奇异值分解
- 🥕求k×n样本主成分矩阵
📚降维
- 降维是对数据高维度特征的一种预处理方法。降维是将高维度的数据保留下最重要的一些特征,去除噪声和不重要的特征,从而实现提升数据处理速度的目的。在实际的生产和应用中,降维在一定的信息损失范围内,可以为我们节省大量的时间和成本。降维也成为了应用非常广泛的数据预处理方法。
- 降维具有如下一些优点:
- 1)使得数据集更易使用;
- 2)降低算法的计算开销;
- 3)去除噪声;
- 4)使得结果容易理解。
- PCA(Principal Component Analysis) 是一种常见的数据分析方式,常用于高维数据的降维,可用于提取数据的主要特征分量。
- PCA 的数学推导可以从最大可分型和最近重构型两方面进行,前者的优化条件为划分后方差最大,后者的优化条件为点到划分平面距离最小,这里我将从最大可分性的角度进行证明。
- 初学者建议先阅读这份教程,英文好的可以直接阅读原文文献,其他小伙伴可以参考:A tutorial on Principal Components Analysis | 主成分分析(PCA)教程
- 奇异值分解,可以参考这份教程,英文好的可以直接阅读原文文献,其他的小伙伴可以参考:A Tutorial on Principal Component Analysis(译)
- PCA是将数据投影到方差最大的几个相互正交的方向上,以期待保留最多的样本信息。
- 样本的方差越大表示样本的多样性越好,在训练模型的时候,我们当然希望数据的差别越大越好。否则即使样本很多但是他们彼此相似或者相同,提供的样本信息将相同,相当于只有很少的样本提供信息是有用的。
- 样本信息不足将导致模型性能不够理想。这就是PCA降维的目的:将数据投影到方差最大的几个相互正交的方向上。这种约束有时候很有用,比如在下面这个例子:

- 对于这个样本集我们可以将数据投影到 x 轴或者 y 轴,但这都不是最佳的投影方向,因为这两个方向都不能最好的反映数据的分布。很明显还存在最佳的方向可以描述数据的分布趋势,那就是图中红色直线所在的方向。也是数据样本作投影,方差最大的方向。向这个方向做投影,投影后数据的方差最大,数据保留的信息最多。
📚 PCA的思想
- PCA顾名思义,就是找出数据里最主要的方面,用数据里最主要的方面来代替原始数据。基本想法是将所有数据投影到一个子空间中,从而达到降维的目标,为了寻找这个子空间,我们基本想法是:
- 所有数据在子空间中更为分散
- 损失的信息最小,即:在补空间的分量少
- PCA问题的优化目标:将一组n维向量降为k维(0<k≤n)其目标是选择k个单位正交基,使得原始数据变换到该组基上后,各特征两两之间的协方差为0,而特征的方差则尽可能大,当在正交的约束下取最大的k个方差。

- 特征选择的问题,其实就是要剔除的特征主要是和类标签无关的特征。而这里的特征很多是和类标签有关的,但里面存在噪声或者冗余。在这种情况下,需要一种特征降维的方法来减少特征数,减少噪音和冗余,减少过度拟合的可能性。
- PCA的思想是将n维特征映射到k维上(k<n),这k维是全新的正交特征。这k维特征称为主成分,是重新构造出来的k维特征,而不是简单地从n维特征中去除其余n-k维特征。
📚用最直观的方式告诉你:什么是主成分分析PCA😄
哔哩哔哩视频网址,呜呜呜强推!(这个视频用的是特征值分解算法)
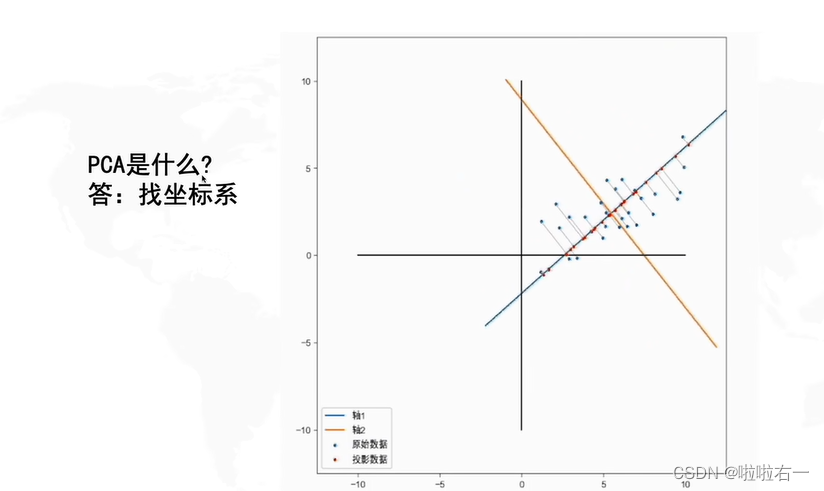
🐇PCA是什么?
- PCA的目的就是找到一个坐标系,使得这个数据在只保留一个维度的时候,信息损失是最小的(数据分布式最分散的,即保留的信息是最多的)。
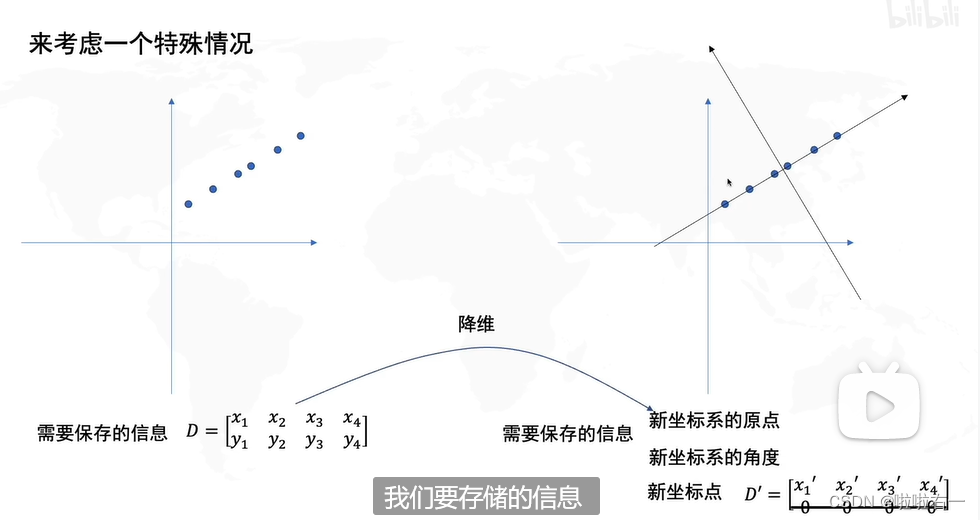
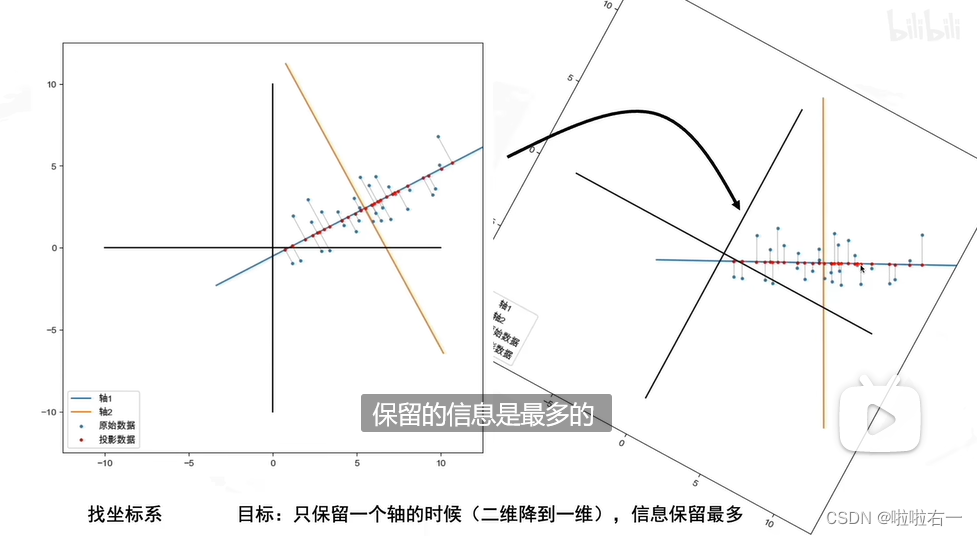
🐇怎么找坐标系,特别是怎么找方差最大的方向?
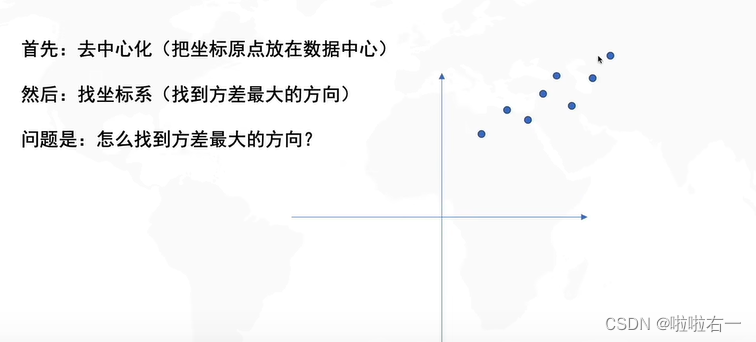
补充数据的线性变换
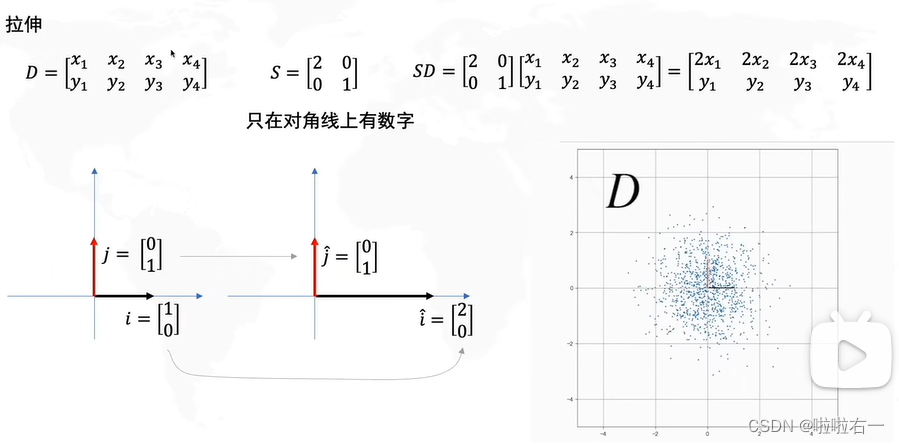
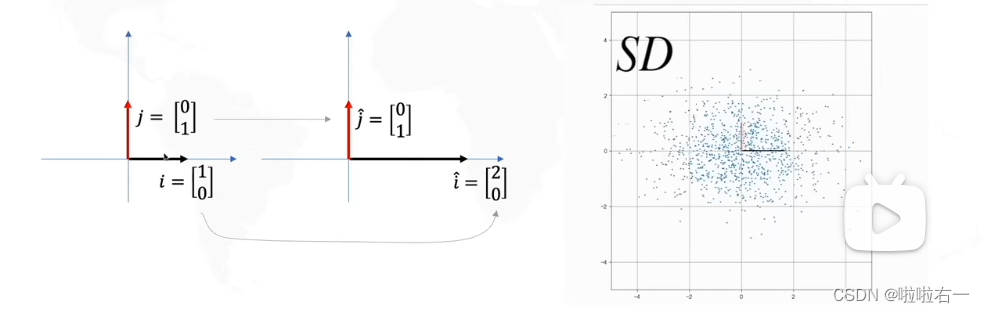
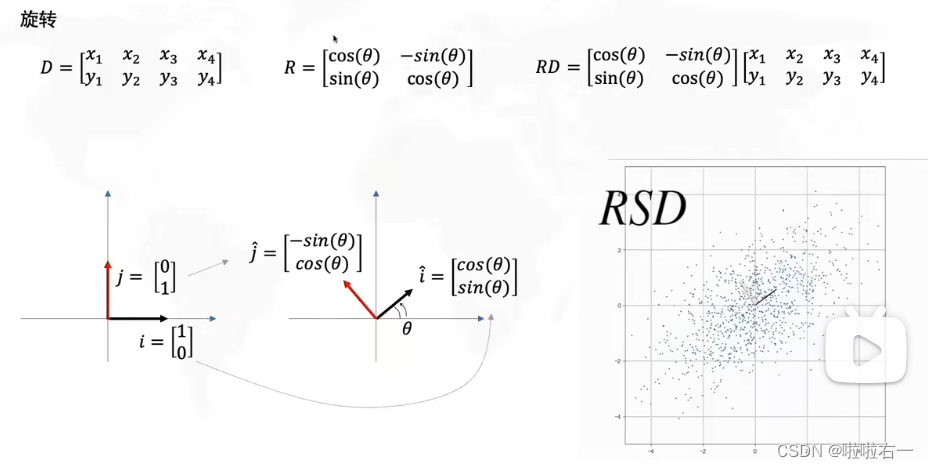
- 左右拉伸的时候,拉伸的方向决定了方差最大的方向是横或者纵。
- 旋转决定了方差最大方向的角度。
- 所以实际上我们要求的就是R,看要转几度。
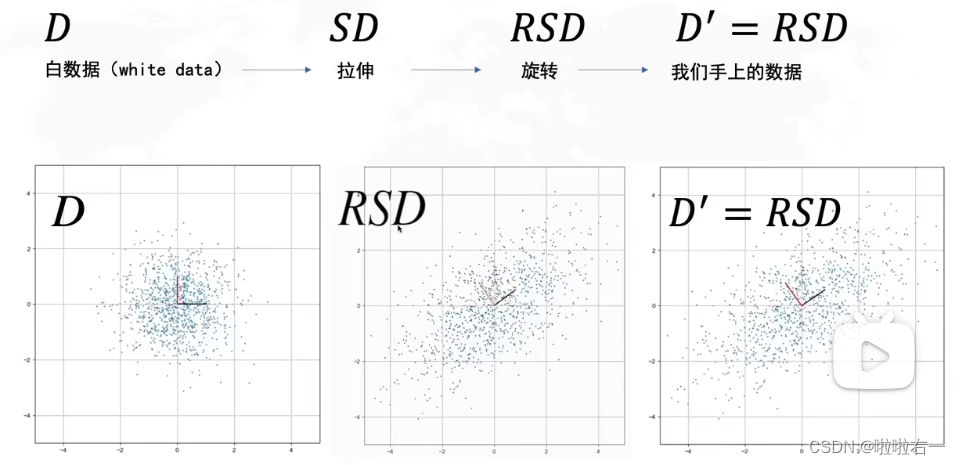
- 上述过程是可逆的
🐇怎么求R?协方差矩阵的特征向量就是R!
🥕协方差

🥕协方差矩阵
- 左边第一个图的协方差是个单位矩阵;第二个对角线是正数,所以是正相关;第三个对角线是负数,所以是负相关。
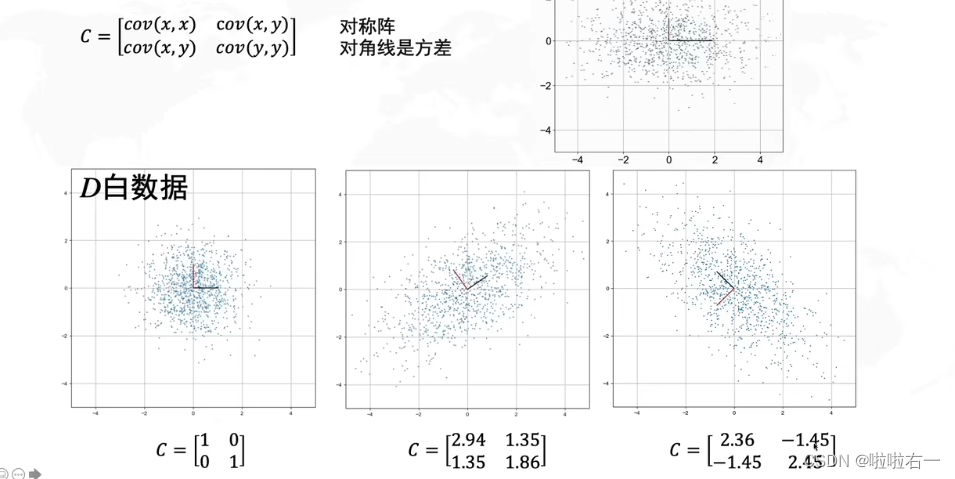
- 将协方差公式和方差公式代入协方差矩阵,可得以下推导。

- 上边是白数据的协方差矩阵,然后代入求我们手上数据的协方差矩阵。

🥕协方差矩阵的特征向量
- 协方差矩阵乘以特征向量等于特征值乘以特征向量
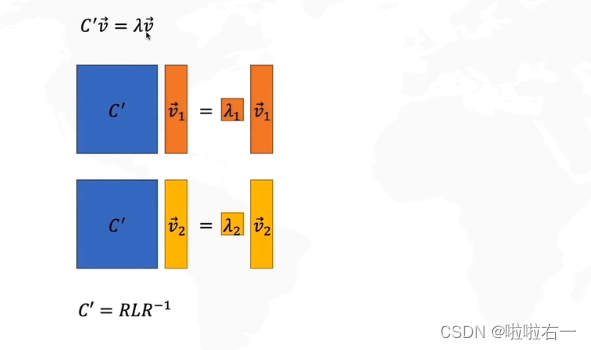
- 转换后,可以视作如下构成:

- 把
特征向量1和特征向量2看作R矩阵,把特征值1和特征值2看作L矩阵,再把左边的R移到右边
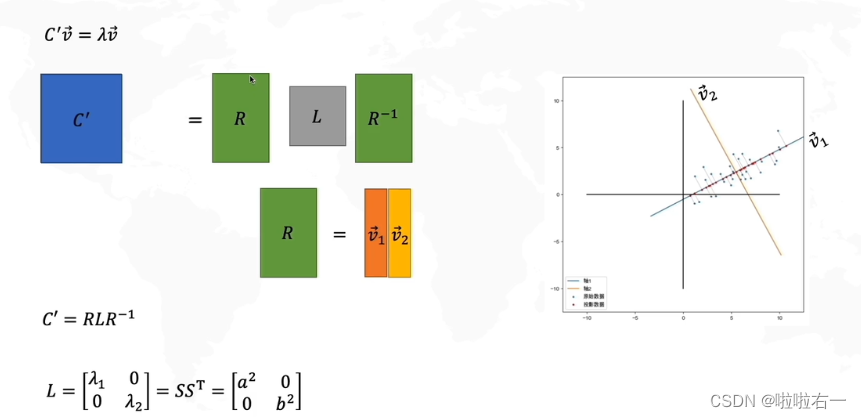
- 由此得:
- 特征值 1就是x方向拉伸倍数的平方,特征值2就是y方向拉伸倍数的平方。
- L就是在R这组基下(新坐标系)的协方差矩阵。
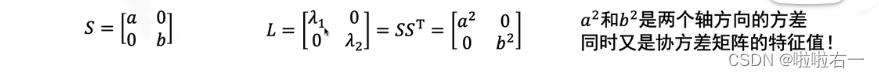
🐇总结一下PCA怎么求解?
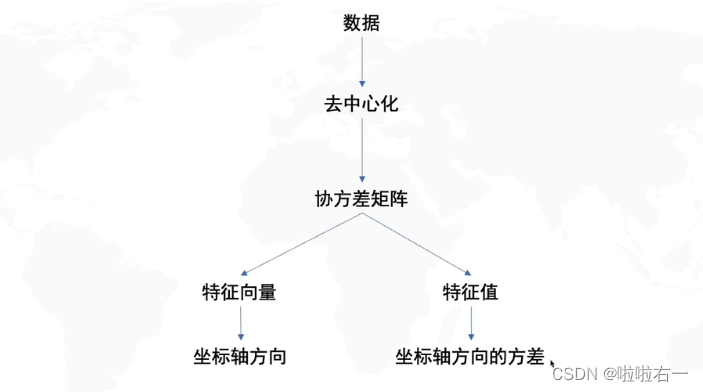
🐇PCA和奇异值分解
- PCA的缺点:离群点影响大。就加一个离群点,整个方向动的幅度就很大。
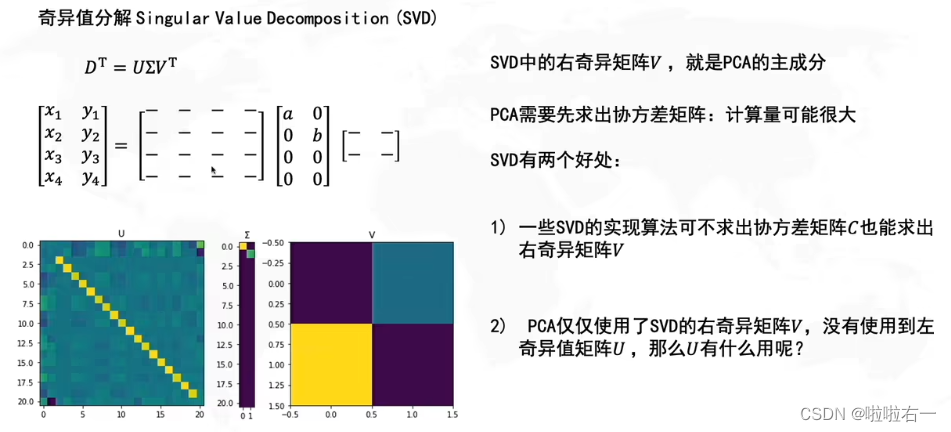
奇异值分解后续补充
接下来是堆公式环节😢
📚PCA的推导:基于最小投影距离
以下公式推导主要参考:刘建平Pinard——主成分分析(PCA)原理总结,详细原理可以阅读:降维——PCA(非常详细)。




📚PCA的推导:基于最大投影方差


📚PCA算法流程⭐️
🐇特征值分解算法
🥕观测数据规范化处理,得到规范化数据矩阵X
🥕计算相关矩阵R
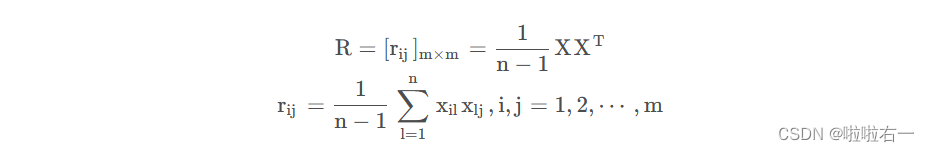
🥕求R的特征值和特征向量

🥕求k个样本主成分
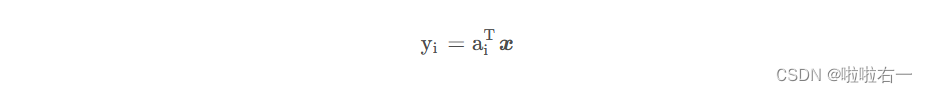
🥕计算k个主成分yi与原变量xi的相关系数ρ(xi,yi)以及k个主成分对原变量xi的贡献率vi
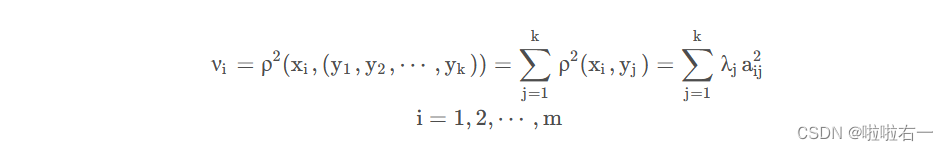
🥕计算n个样本的k个主成分值

以上部分参考了sklearn基础篇(九)-- 主成分分析(PCA),不过结合那个哔哩哔哩视频,个人感觉PCA这一算法的流程其实就是:
- 数据预处理:将原始数据进行标准化或归一化处理,完成去中心化。
- 计算协方差矩阵:将处理后的数据进行协方差矩阵的计算,得到协方差矩阵。
- 特征值分解:对协方差矩阵进行特征值分解,得到特征值和特征向量。
- 特征值排序:将所有特征值从大到小排序,选择前k个特征值对应的特征向量作为新的基向量。
- 生成新的特征空间:将原始数据投影到新的特征空间中,得到降维后的数据。包括拉伸(特征值)和旋转(特征向量)。
🐇PCA实例
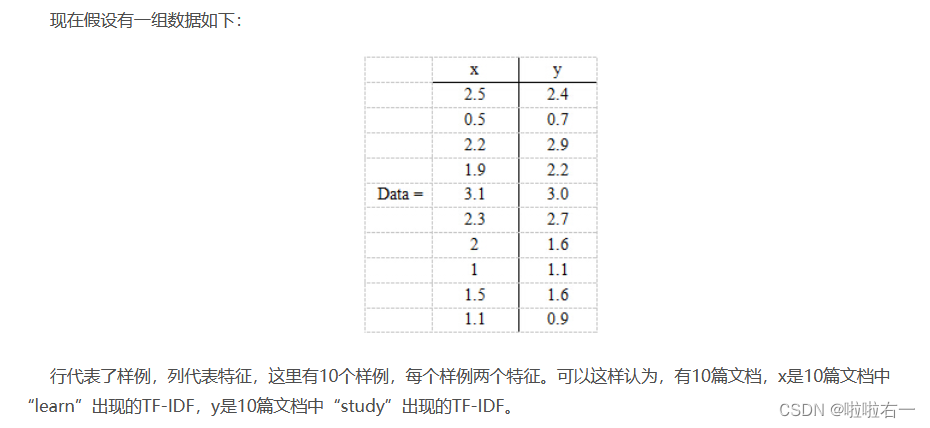
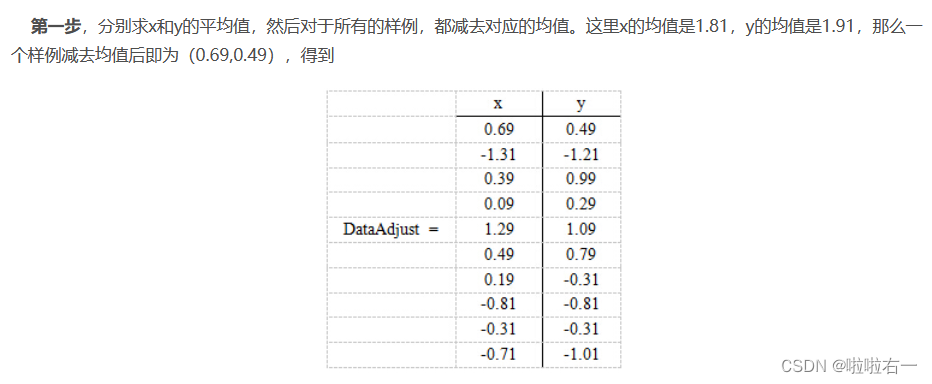



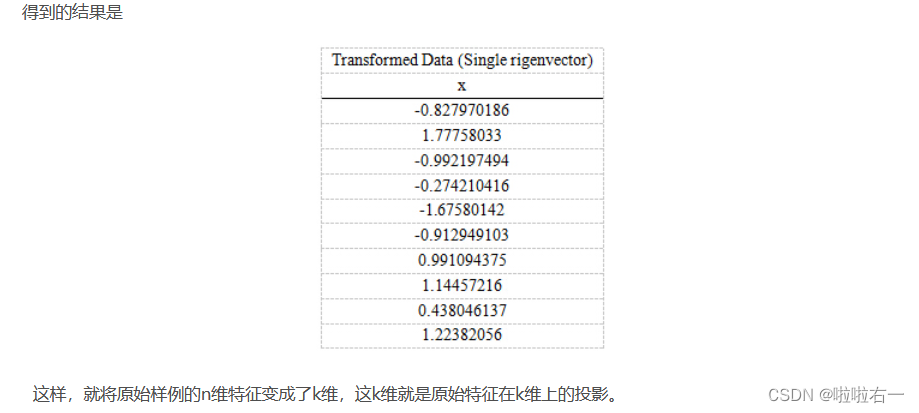
🐇奇异值分解算法
输入:m×n样本矩阵X,每一行元素均值为0。这里每一行是一个特征。
输出:k×n样本主成分矩阵Y
参数:主成分个数k
🥕构造新的n×m矩阵
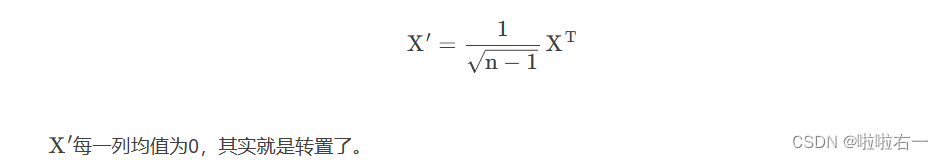
🥕对矩阵X′进行截断奇异值分解
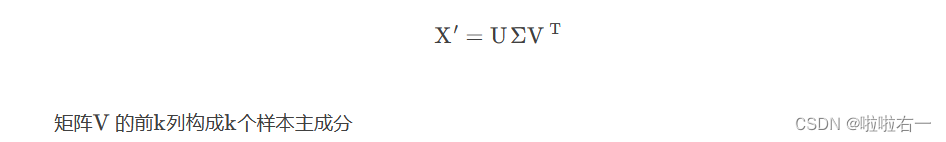
🥕求k×n样本主成分矩阵