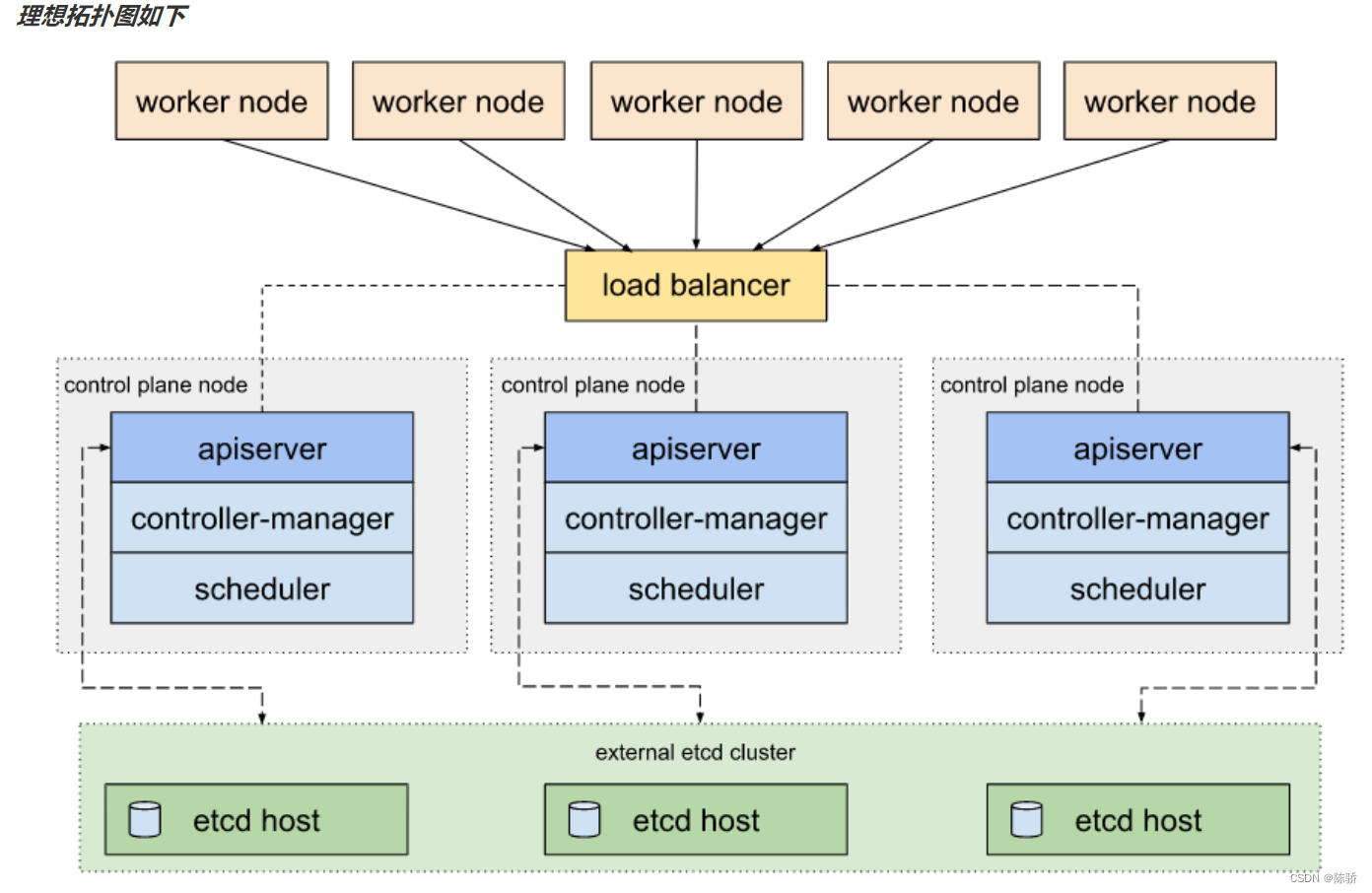
[CF复盘] Codeforces Round 874 (Div. 3 20230520
- 总结
- A. Musical Puzzle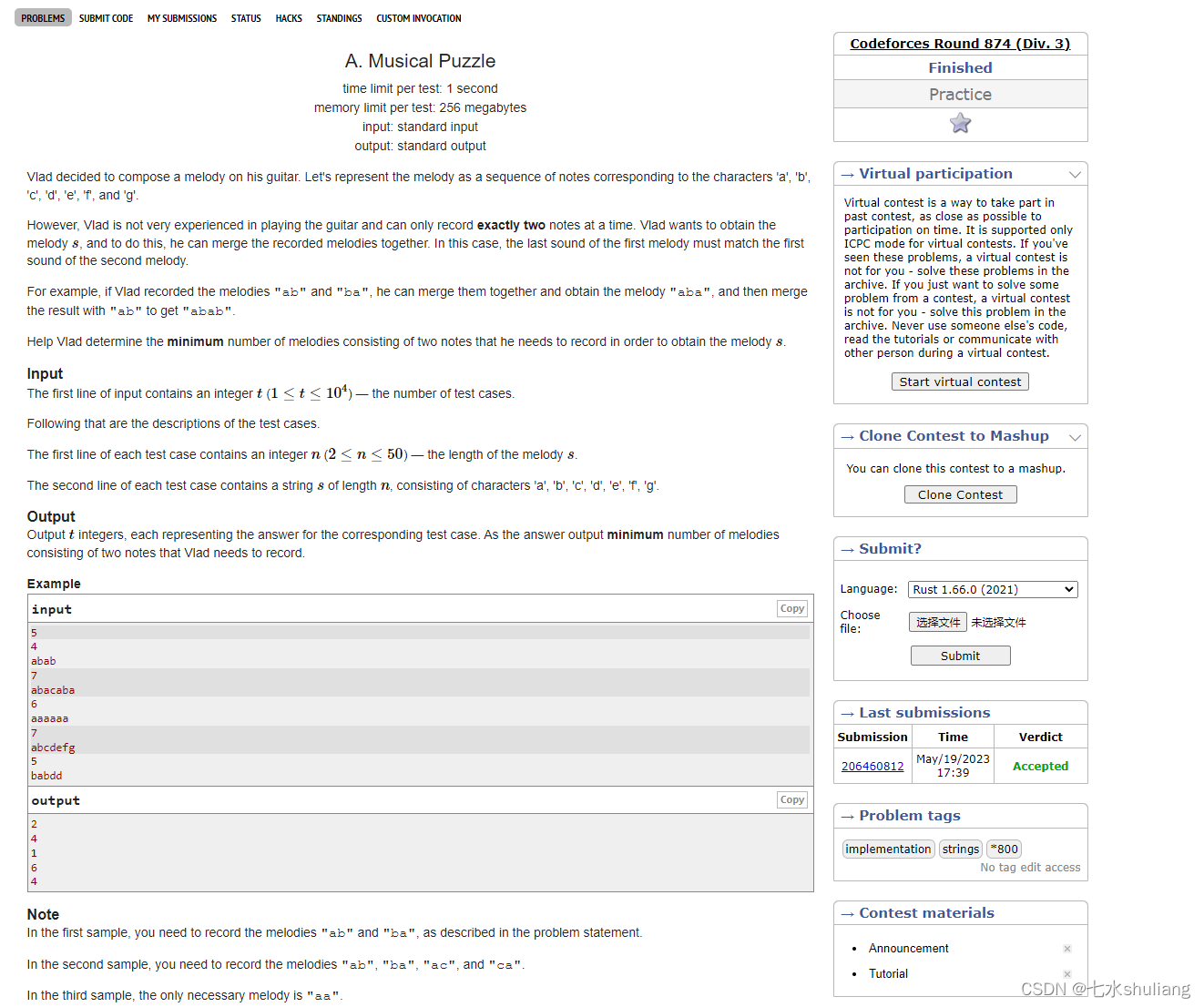
- 2. 思路分析
- 3. 代码实现
- B. Restore the Weather
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- C. Vlad Building Beautiful Array
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- D. Flipper
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- E. Round Dance
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
- F. Ira and Flamenco
- 1. 题目描述
- 2. 思路分析
- 3. 代码实现
总结
- G好像lc出过,F卡一小时,G不想补了。
- A模拟
- B贪心
- C模拟
- D贪心+分类讨论
- E贪心+并查集
- F逆元+前缀乘
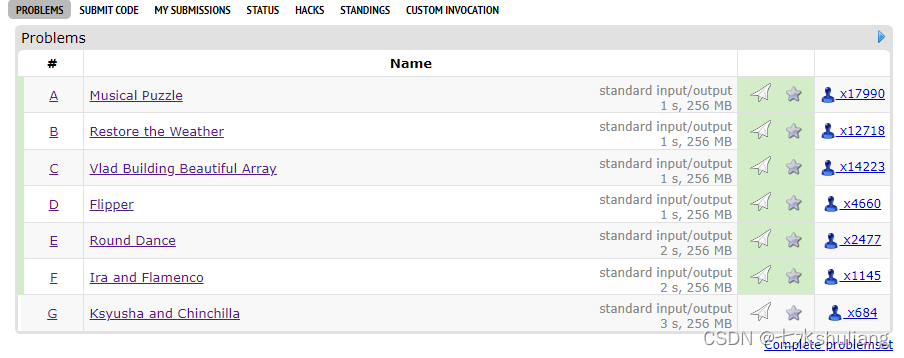
A. Musical Puzzle
2. 思路分析
3. 代码实现
PROBLEM = """用长度为2的字符串组合出整个串s,要多少种不同的串
"""
# ms
def solve():
n, = RI()
s, = RS()
p = set()
for i in range(n - 1):
p.add(s[i:i + 2])
print(len(p))
B. Restore the Weather
链接: B. Restore the Weather
1. 题目描述
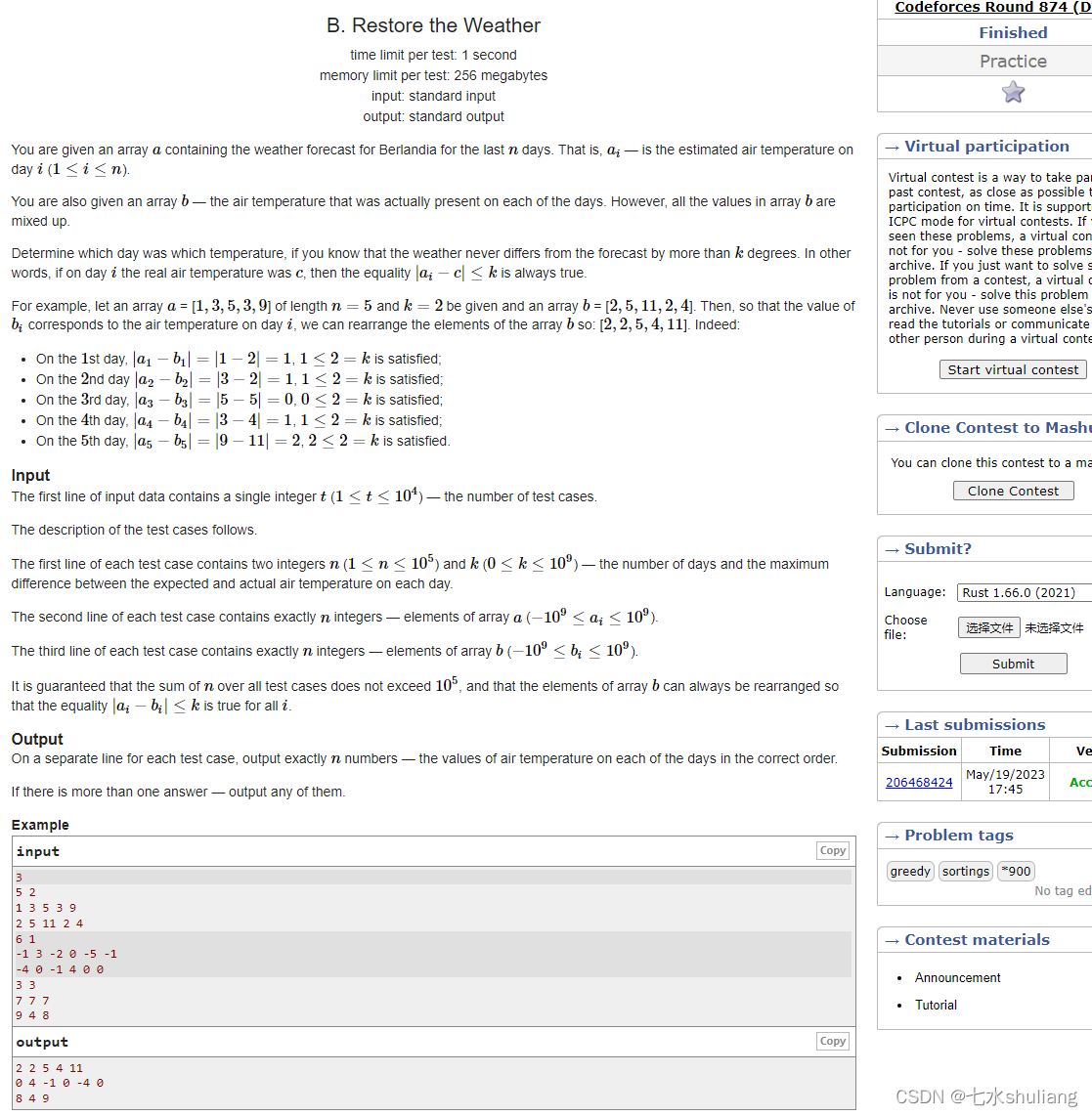
2. 思路分析
3. 代码实现
PROBLEM = """输入n、k和长为n的数组a、b。
a[i]代表第i天预测的气温。
b[i]代表第i天实际气温。但是b被打乱了。
已知每天的abs(预测值-实际值)<=k。
请还原出一个正确的b。数据保证有解
"""
"""贪心思考,优先匹配大的或者小的值即可。由于数据保证有解,k实际没用。
为了代码方便,从大的开始匹配,这样b就可以一直pop
"""
# ms
def solve():
n, k = RI()
a = RILST()
b = RILST()
b.sort()
ans = [0] * n
for i in sorted(range(n), key=lambda x: -a[x]):
ans[i] = b.pop()
print(*ans)
C. Vlad Building Beautiful Array
链接: C. Vlad Building Beautiful Array
1. 题目描述
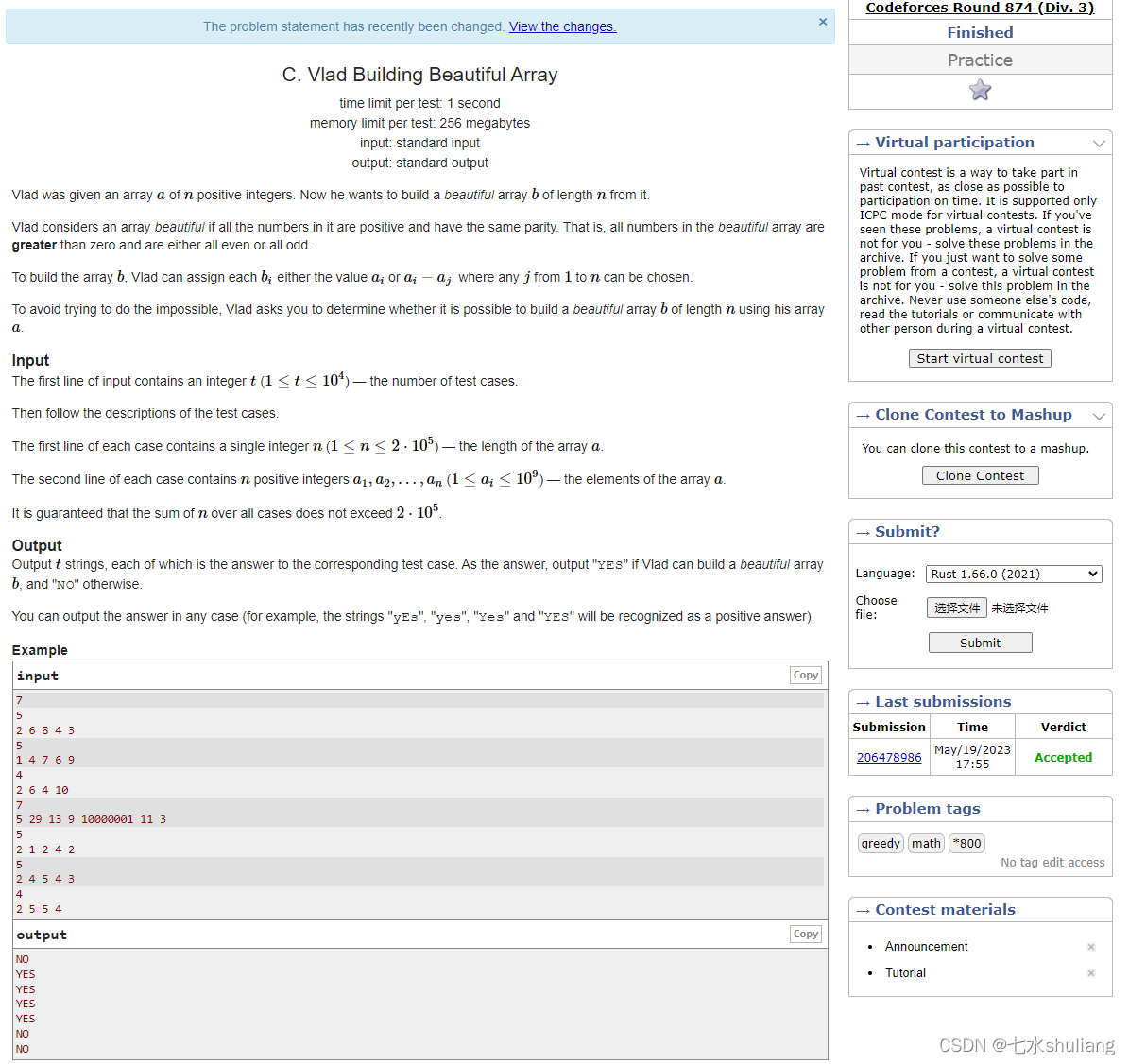
2. 思路分析
3. 代码实现
PROBLEM = """输入n和n个正整数a[i]。
构造一个长为n的数组b。
其中b[i]要么等于a[i],要么等于a[i]-a[j]。其中j随便选1~n。
要求b中所有数据奇偶性相同。
"""
"""分别尝试奇数或者偶数即可。
这题灵神还挖掘了更多性质,其实代码可以很短,只讨论最小的奇数即可。
但比赛中没必要深挖,直接写即可"""
# ms
def solve():
n, = RI()
a = RILST()
even, odd = [], []
for v in a:
if v & 1:
odd.append(v)
else:
even.append(v)
if not even or not odd:
return print("YES")
even.sort()
odd.sort()
def try_1():
for i, v in enumerate(a):
if v & 1:
continue
if odd[0] >= v:
return False
return True
def try_2():
for i, v in enumerate(a):
if not v & 1:
continue
if odd[0] >= v:
return False
return True
if try_1() or try_2():
return print("YES")
print("NO")
D. Flipper
链接: D. Flipper
1. 题目描述
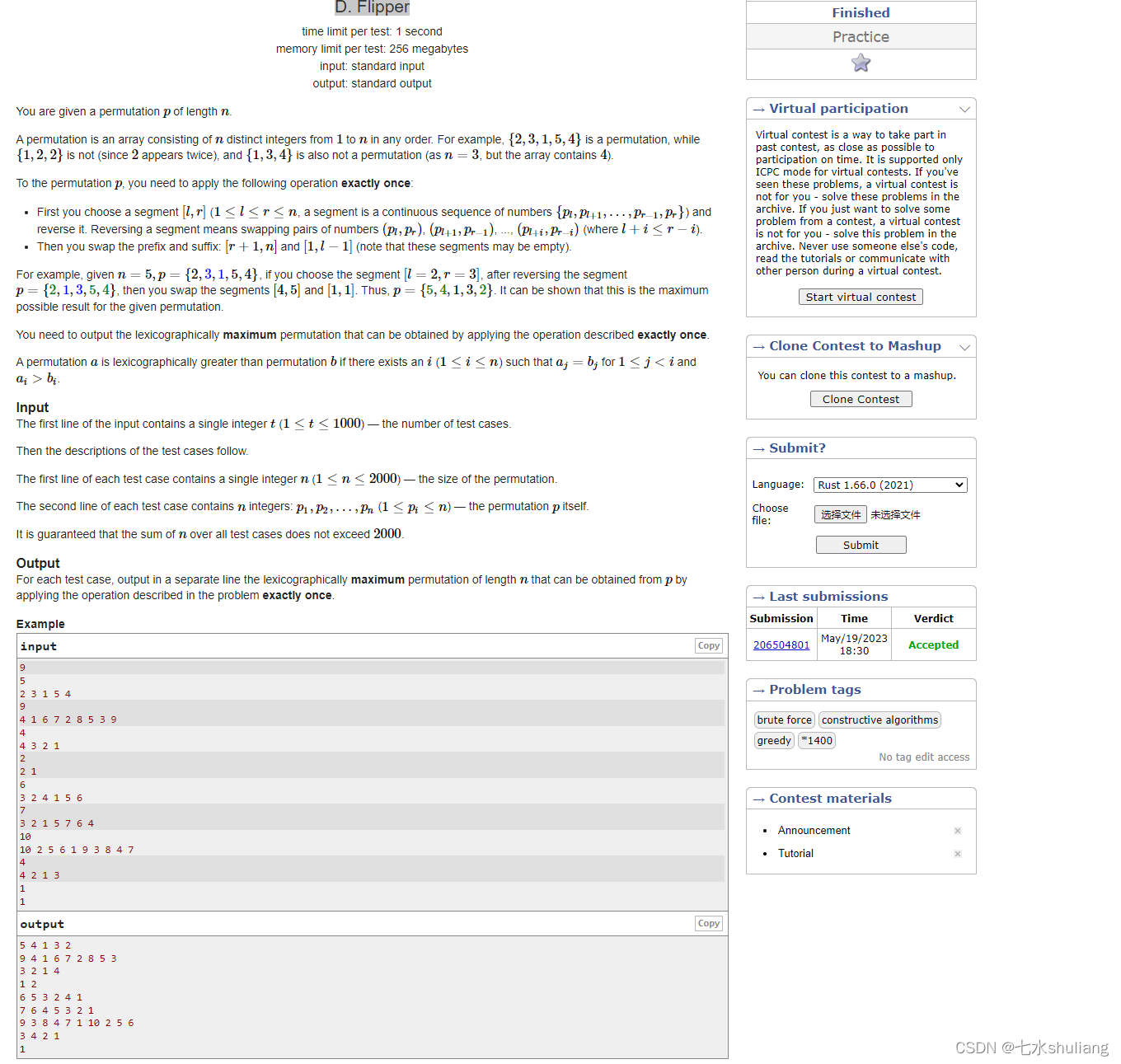
2. 思路分析
3. 代码实现
PROBLEM = """给一个长为n的排列p。你必须做如下操作恰好一次:
1. 选一个子段[l,r],(1<=l<=r<=n)翻转这个段。
2. 把这个段两边的数据交换。即交换[1~l-1],[r+1,n],注意这两段可以为空
输出操作后字典序最大的p
"""
"""贪心,枚举l即可。注意讨论
- 先找最大的数即n的位置pos,让pos作为r,枚举l。若n在最后,则可以作为r,直接翻转到0.
- 若n在0上,由于必须翻转一次,n一定会向后, 那么考虑让n-1到0,方法和前边一样。
---
- 这题也有O(n)的做法。可以看看灵神的视频。
找到pos后,前边段其实是不变的,r翻转后也是不变的。讨论r-1即可。
"""
# ms
def solve():
n, = RI()
p = RILST()
if n == 1:
return print(1)
ans = p[::-1]
pos = p.index(n)
if pos:
ans = max(ans, p[pos+1:]+p[pos:] + p[:pos])
mx = []
r = pos
for l in range(pos):
mx = max(mx, p[l:r][::-1] + p[:l])
ans = max(ans, p[pos:] + mx)
else:
pos = p.index(n - 1)
ans = max(ans, p[pos+1:]+p[pos:] + p[:pos])
mx = []
r = pos
for l in range(pos):
mx = max(mx, p[l:r][::-1] + p[:l])
ans = max(ans, p[pos:] + mx)
print(*ans)
E. Round Dance
链接: E. Round Dance
1. 题目描述
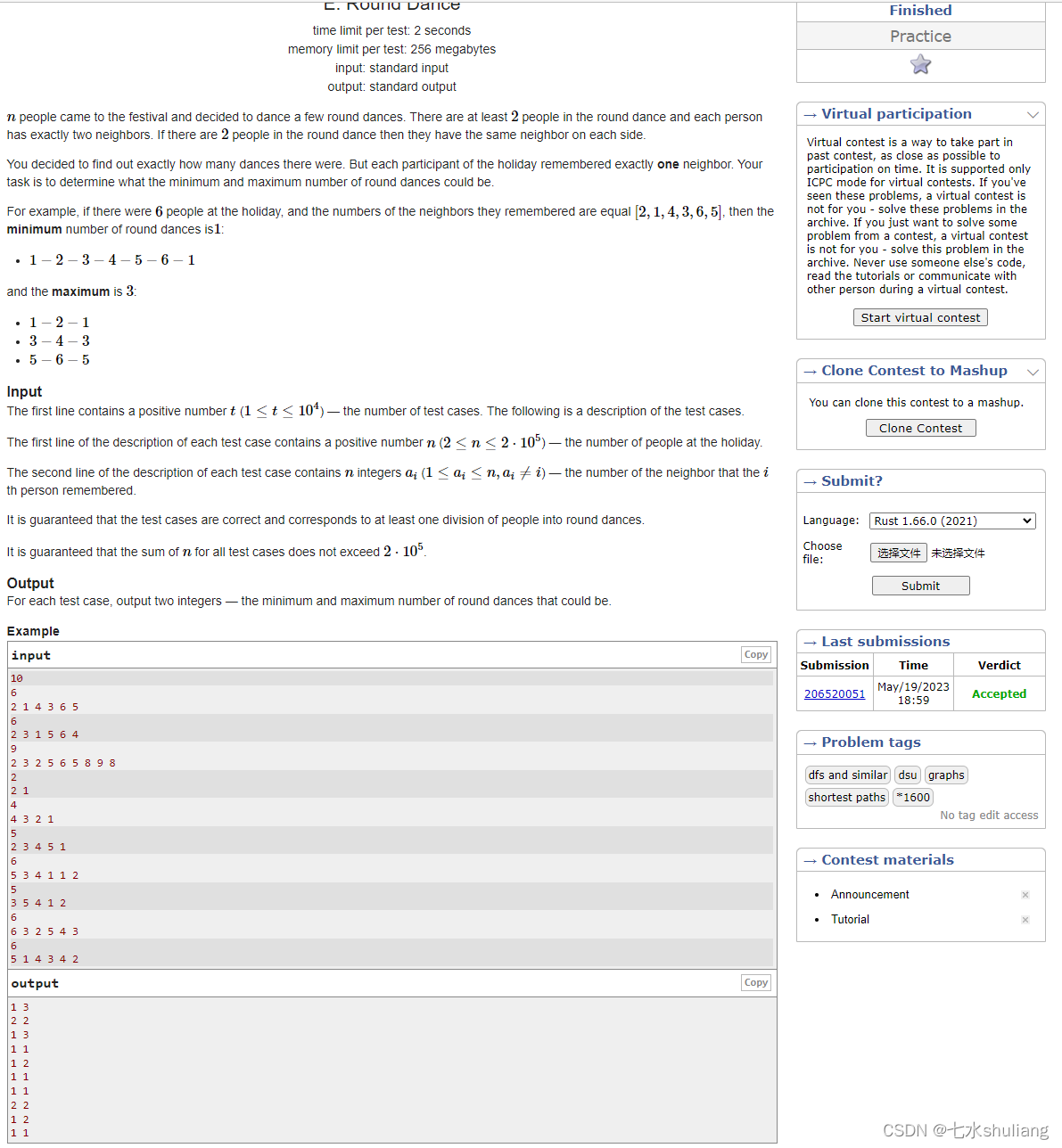
2. 思路分析
3. 代码实现
PROBLEM = """给出n和长为n的数组a[i].其中a[i]是i的一个邻居。
已知每个i其实有2邻居,整体组成多个环。
问最少、最多有几个环。
"""
"""并查集。
直接按已知邻居合并。最后有几个家族,最多就有几个环。
最少怎么讨论呢。
- 已知的边合并时,若x,y已经在一个环里了,要么是x连过y,要么是z连过y,且z和x已经连接。显然第二种情况会导致这个环闭合。
- 那么这就可以计算一个封闭的环。先计算出有多少个封闭的环。cc
- 再计算有多少个点在非封闭的家族里。(这里计算有1个即可,因为是讨论最少),把所有非封闭的点连成1个环。op
- mn=cc+op
"""
class DSU:
def __init__(self, n):
self.fathers = list(range(n))
self.size = [1] * n # 本家族size
self.edge_size = [0] * n # 本家族边数(带自环/重边)
self.n = n
self.setCount = n # 共几个家族
def find_fa(self, x):
fs = self.fathers
t = x
while fs[x] != x:
x = fs[x]
while t != x:
fs[t], t = x, fs[t]
return x
def union(self, x: int, y: int) -> bool:
x = self.find_fa(x)
y = self.find_fa(y)
if x == y:
# self.edge_size[y] += 1
return False
# if self.size[x] > self.size[y]: # 注意如果要定向合并x->y,需要干掉这个;实际上上边改成find_fa后,按轶合并没必要了,所以可以常关
# x, y = y, x
self.fathers[x] = y
self.size[y] += self.size[x]
self.edge_size[y] += 1 + self.edge_size[x]
self.setCount -= 1
return True
# ms
def solve():
n, = RI()
a = RILST()
dsu = DSU(n)
c = set() # 环内的点
vis = set()
for i, v in enumerate(a):
if not dsu.union(i, v - 1) and (v - 1, i) not in vis:
c.add(dsu.find_fa(i))
vis.add((i, v - 1))
cc = set() # 每个环的代表元
for p in c:
cc.add(dsu.find_fa(p))
op = set() # 不在环的点
for i in range(n):
if dsu.find_fa(i) not in cc:
op.add(i)
break # 只要一个就行
if not op:
mn = len(cc)
elif not cc:
mn = 1
else:
mn = len(cc) + 1
# print(cc,op)
print(mn, dsu.setCount)
F. Ira and Flamenco
链接: F. Ira and Flamenco
1. 题目描述
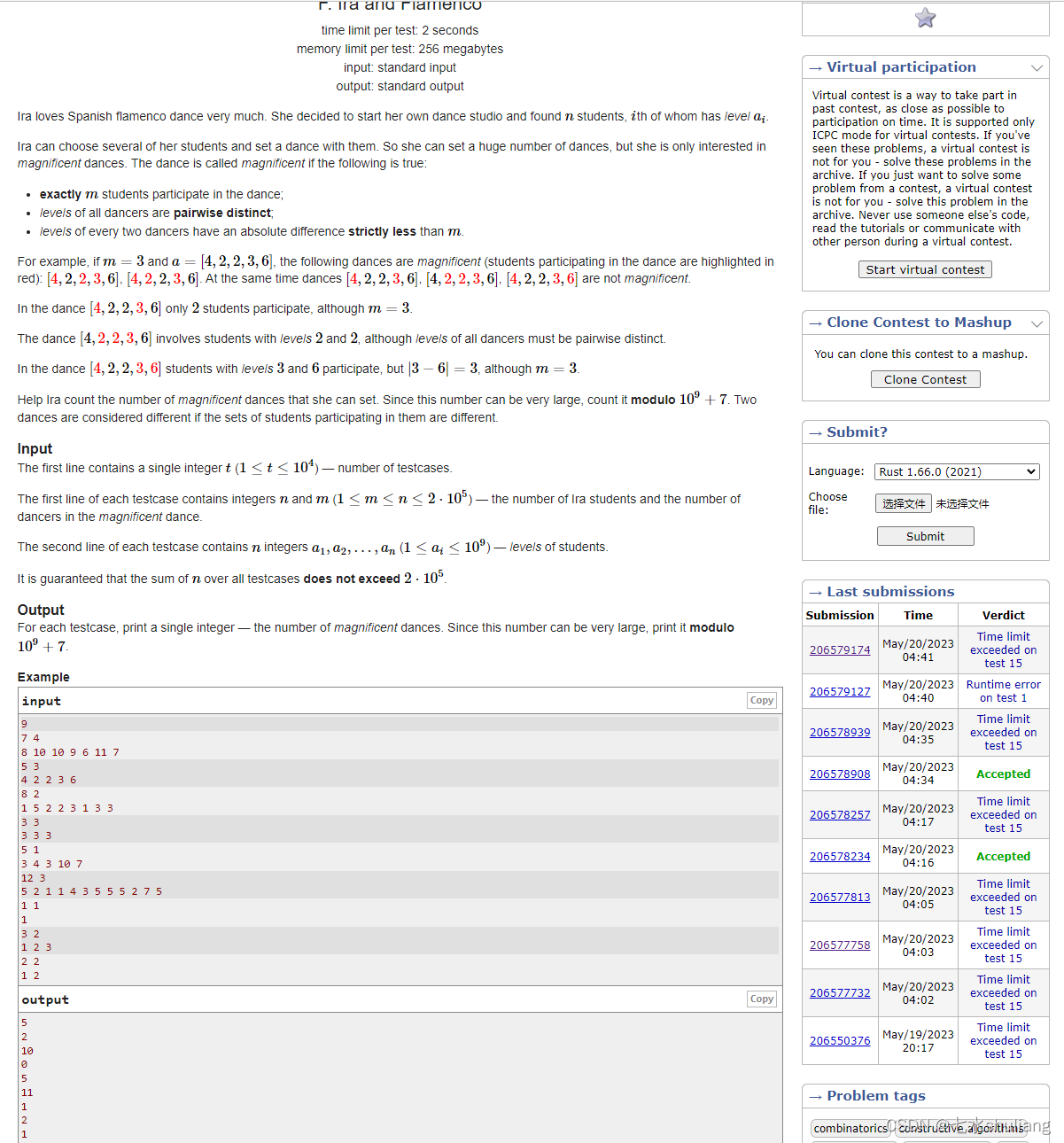
2. 思路分析
3. 代码实现
MOD = 10 ** 9 + 7
PROBLEM = """输入n,m和长为n的数组a[i]。
你需要从中选m个数。其中每两个数都不同,且每两个数的差值严格小于m。
问有多少种方案。下标不同则视为不同方案。
"""
"""逆元/区间乘/乘法原理
看错题很久, 后来发现严格选m个数,且差值小于m,那只能选一段连续的数字。
每个数字有cnt[x]个,那么乘法原理计算即可。剩下的问题就是区间乘怎么弄。
可以滑窗,维护长为m的段,合法情况是段首段尾的值正好差m-1。
每次乘上窗右侧,除去窗左侧出窗的数即可,由于除法不满足同余,因此要乘逆元logn。
但直接预处理前缀乘,就可以O(n)计算每个逆元。
---
赛后卡哈希了,哭了
"""
# ms
def solve():
n, m = RI()
a = RILST()
cnt = Counter(a)
b = sorted((k, v) for k, v in cnt.items())
fact = [1]
for c,v in b:
fact.append(fact[-1] * v % MOD)
inv = [1] * len(fact)
inv[-1] = pow(fact[-1], MOD - 2, MOD)
for i in range(len(b) - 1, -1, -1):
inv[i] = b[i][1] * inv[i + 1] % MOD
ans = 0
for i in range(m - 1, len(b)):
j = i - m + 1
if j >= 0 and b[j][0] == b[i][0] - m + 1:
ans = (ans + fact[i + 1] * inv[j]) % MOD
print(ans % MOD)