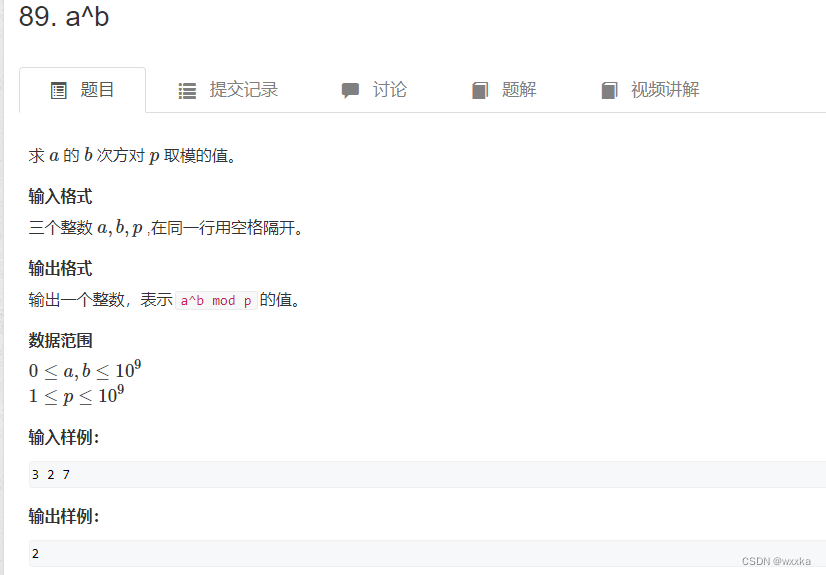
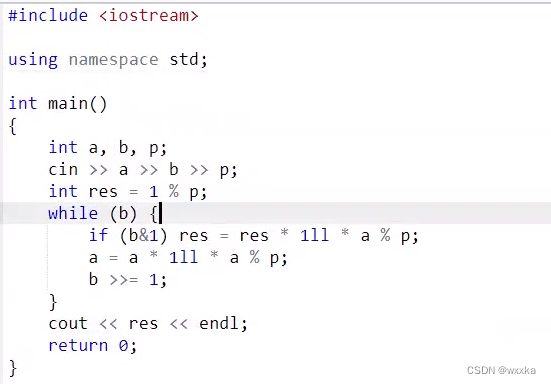
快速幂

#include<bits/stdc++.h>
using namespace std;
//126348976 982638476 938420413
int main(){
    int a,b,p;
    cin>>a>>b>>p;
    long long res = 1,ci=1;
    int flag=0;
    if(b==0){
            res%=p;
        }
    else{
        while(b){
    	if (flag==0)ci=a%p;
    	else
          ci=(ci%p)*(ci%p)%p;
        
		if (b&1)res=(res*(ci%p))%p;
        b>>=1;
        flag++;
        //cout<<ci<<"  "<<res<<endl;
    }
    }
    cout<<res<<endl;
    return 0;
}

64位整数乘法

#include<bits/stdc++.h>
/*
a*b=a+a+a+...+a
a*1=a
a*2=2a
a*4=4a;
...
a*(2^k)=2^k*a;
*/
using namespace std;
typedef long long LL;
int main(){
    LL a,b,p;
    cin>>a>>b>>p;
    LL res=0;
    while(b){
        if(b&1)res=(res+a)%p;
        b>>=1;
        a=a*2%p;
    }
    cout<<res<<endl;
    return 0;
}

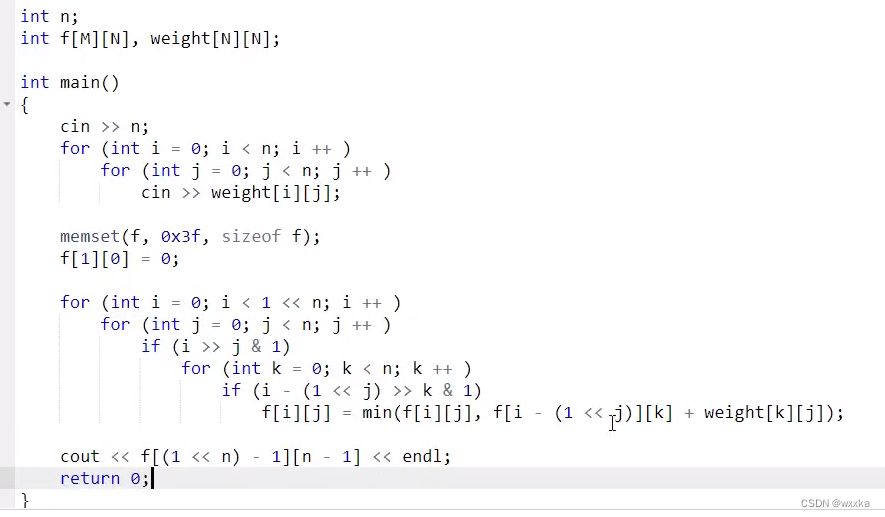
最短Hamilton路径

1s约计算1亿次；

 f[state][j]=

f[state_k][j]+weight[k][j];

state_k是state除去j之后的集合，state_k要包含k，k是state_k二进制表示中为1的下标，枚举出k

state_k=state-2^j;

for (int j = 0;j < 点数;j++){//n点数

        if ((state_k>>j )& 1 == 0)

          {    

                state=state_k+2^j;

                f[state][j]=f[state_k][j]+weight[k][j];

          }

}

 

#include <bits/stdc++.h>

using namespace std;
const int N=20,M=1<<20; 
int n;
int f[M][N],weight[N][N];
int main(){
	cin>>n;
	for(int i = 0;i < n;i++)
		for(int j = 0;j < n;j++){
			cin>>weight[i][j];
		}
		
	memset(f,0x3f,sizeof(f));
	f[1][0]=0;
	for(int i = 0;i < 1<<n;i++)//枚举所有的状态 
		for(int j = 0;j < n;j++){//枚举状态i二进制表示中所有的1的位置 
			if(i>>j & 1)
				for(int k = 0;k < n;k++)//枚举状态i去掉第j位后的剩余的1的位置 
					if(i-(1<<j) >> k & 1)//第k位是1 
						f[i][j]=min(f[i][j],f[i-(1<<j)][k]+weight[k][j]);
		}
	cout<<f[(1<<n)-1][n-1]<<endl;
	return 0;
}

汉诺塔问题（三塔）

#include <bits/stdc++.h>
using namespace std;
//f(x)=2^x-1
int hnt(int st,int mid,int dst,int n){
	if(n==1){
		//cout<<"from "<<char(st)<<" through "<<char(mid)<<" to "<<char(dst)<<" with "<<n<<endl;
		return 1;
	}
	else {
		int sum=0;
		cout<<"from "<<char(st)<<" through "<<char(dst)<<" to "<<char(mid)<<" with "<<n-1<<endl;
		sum+=hnt(st,dst,mid,n-1);
		cout<<"from "<<char(st)<<" through "<<char(mid)<<" to "<<char(dst)<<" with "<<1<<endl;
		sum+=hnt(st,mid,dst,1);
		cout<<"from "<<char(mid)<<" through "<<char(st)<<" to "<<char(dst)<<" with "<<n-1<<endl;
		sum+=hnt(mid,st,dst,n-1);
		return sum;
	}
}
int main(){
	int st,mid,dst,n;
	st=int('A'),mid=int('B'),dst=int('C');
	n=12;
	int ans = hnt(st,mid,dst,n);
	cout<<ans;
	return 0;
} 

四塔汉诺塔问题

// 凡是用到min的都需要，赋较大值。
    // memset以字节形式重置(int: 0x3f3f3f3f)
    //又0x3f的2倍为最大整数,所以还可以满足加法不越界

#include<bits/stdc++.h>

using namespace std;
const int N=15;
int d[N],f[N];
int main(){
    d[1]=1;
    for(int i = 2;i <=12;i++ )
    d[i]=d[i-1]+1+d[i-1];
    memset(f,0x3f,sizeof(f));
    f[0]=0;
    f[1]=1;
    //先让i个盘到B塔或者C塔，剩下的n-i盘在3塔情况下移到D
//再将i盘在4塔(因为D塔都是更重的盘)情况下移动到D。因为对于i我们不知道哪个最优，因此
//因此推导为 f[n] = min(f[n],2*f[i]+d[n-i])(for i in [1..n-1])
	for(int i =2;i <= 12;i++)
		for(int j = 1;j < i;j++)
			f[i]=min(f[i],f[j]+d[i-j]+f[j]);
	for(int i =1;i <= 12;i++)
		cout<<f[i]<<endl;
    
    
    return 0;
}