目录
- 知识蒸馏
- 原理
- 概念
- 技巧
- 举例说明
- KL 散度及损失
- KD训练代码
- 导入包
- 网络架构
- teacher网络
- student网络
- teacher网络训练
- 定义基本函数
- 训练主函数
- student网络训练(重点)
- 理论部分
- 定义kd的loss
- 定义基本函数
- 训练主函数
- 绘制结果
- teacher网络的暗知识
- softmax_t
- 推断
- 本质
知识蒸馏是一种很常见的模型轻量化的方法,这里对他的背后原理和代码进行整理。文章比较长,按照自己的需求查阅~
知识蒸馏
原理
概念
知识蒸馏是一种模型压缩的有效解决方案;总的来说,学生模型通过蒸馏训练来获取教师知识,小模型学习到了大模型的泛化能力,保留了大模型的性能,同时降低了模型的大小和复杂性,模型更轻量易于部署。
首先训练一个性能较好的教师(大)模型;使用其输出作为软标签,真实标签作为硬标签;两者联合训练学生模型。【student是根据teacher的结构做一些修剪得到的小网络】
知识蒸馏最早是针对图像分类问题,教师模型最后的softmax层输出的是对应的概率值,相对GT(硬标签)来说,这个概率值的表示有更高的熵,更小的梯度变化,能体现出更丰富的信息。所以学生模型可使用更少的数据和更大的学习率。【收敛很快】
流程
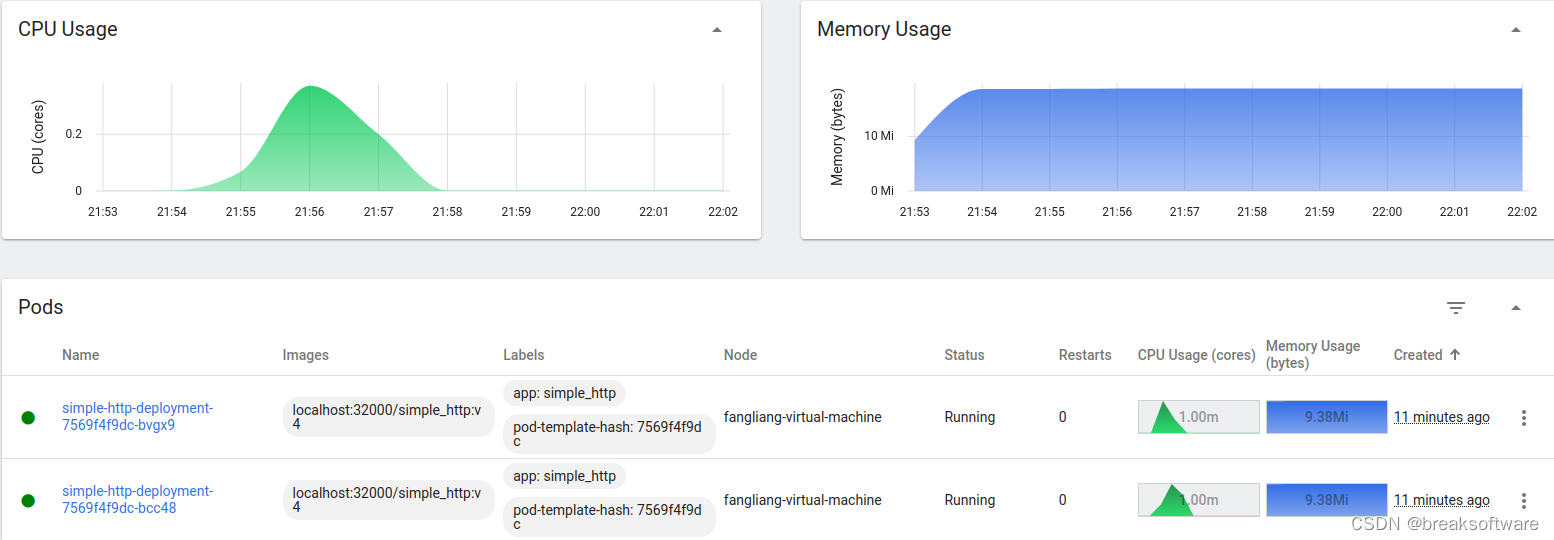
student network是去拟合teacher的结果,可以使用Ensemble的网络作为teacher,这样表现得结果更好。
技巧
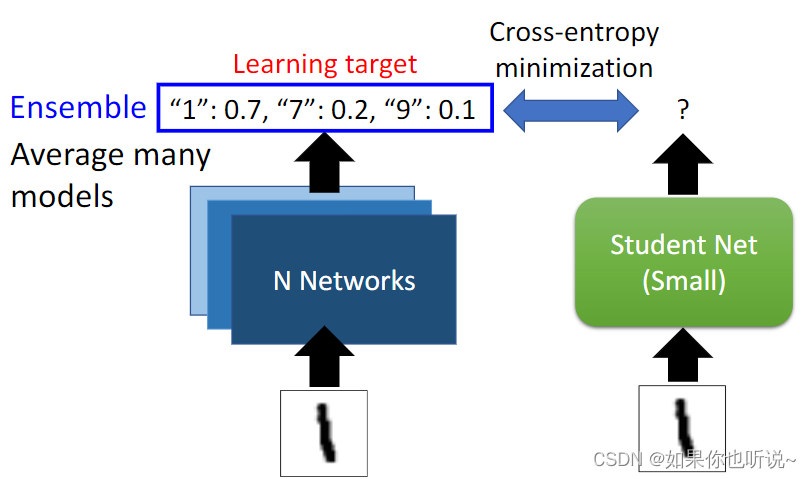
在使用知识蒸馏时有一个小技巧,可以稍微改一下Softmax的函数,T是一个超参数,可以使得函数点更加平滑。因为student要学习teacher给的结果,并且teacher给的结果要告诉student,哪些类别比较相似,而不是直接给出1,0,0(和真实结果没有差别),所以teacher 的输出不应该过度集中,需要更加平滑。这样分类结果不同,但是student学习更加有意义。这个T也就是温度系数,T为1时,和普通的Softmax没有差别,T越高,softmax的output probability distribution越趋于平滑,其分布的熵越大。
同时不一定要用softmax之后的结果去拟合student,完全可以使用之前的,或者类似student的第6层拟合teacher的12层,第3层拟合teacher的第6层,这样结果往往会更好。
举例说明
通常模型Teacher比模型Student更强,在模型Teacher的帮助下,模型student可以"青出于蓝而胜于蓝"😉,因为从计算资源的角度上庞大的模型部署有很多问题,所以通过知识蒸馏可以训练一个相似的小模型去拟合大模型的训练效果,这样预测和部署会便捷很多。同时使用知识蒸馏的方法可以让小模型学到样本之间的相似关系。

这里不仅仅知道西红柿是真实标签,还可以知道这个样本和柿子这个标签很相似,这样可以获取更多信息,这是蒸馏更有价值的地方。
KL 散度及损失
两个网络得到的结果是两个分布,如何去衡量两者是否一致,这里就会用到散度。
KL散度,也叫相对熵,全称是Kullback-Leibler Divergence。是两个概率分布间差异的非对称性度量,可以用来衡量同一个随机变量的两个不同分布之间的距离。
具体的公式为
D
K
L
(
p
∥
q
)
=
∑
i
=
1
n
p
(
x
i
)
l
o
g
(
p
(
x
i
)
q
(
x
i
)
)
D_{KL}(p \Vert q) = \sum_{i=1}^{n}p(x_i)log(\frac{p(x_i)}{q(x_i)})
DKL(p∥q)=i=1∑np(xi)log(q(xi)p(xi))
当p为0时定义
0
l
o
g
0
=
0
0log0=0
0log0=0
如果想了解更多,可以看看这里,稍微总结一下信息熵,交叉熵,KL散度,以及它们之间的联系。不关心的话就PASS。
- 信息熵: − ∑ i = 1 n p ( x i ) l o g ( p ( x i ) ) -\sum_{i=1}^{n}p(x_i)log(p(x_i)) −∑i=1np(xi)log(p(xi)) 衡量一个分布的不确定性,熵越大,不确定性越大。
- 交叉熵: − ∑ i = 1 n p ( x i ) l o g ( q ( x i ) ) -\sum_{i=1}^{n}p(x_i)log(q(x_i)) −∑i=1np(xi)log(q(xi))
- 从公式可以看出来它们的关系:KL散度 = p与q的交叉熵 - q的信息熵。
也就是说,q(x)能在多大程度上表达p(x)所包含的信息,KL散度越大,表达效果越差。K-L散度能帮助我们度量使用一个分布来近似另一个分布时所损失的信息量。
KL散度具有非对称性和非负性:
- 如果P,Q不是完全一致的话 D K L ( p ∥ q ) ≠ D K L ( q ∥ p ) D_{KL}(p \Vert q) \neq D_{KL}(q \Vert p) DKL(p∥q)=DKL(q∥p),所以KL散度是非对称的。
- D K L ≥ 0 D_{KL} \geq0 DKL≥0,如果P,Q完全一致的话,KL散度才会等于0。
有真实分布时,使用交叉熵,没有真实分布时使用KL散度;其实当真实分布信息熵为0(分布确定),此时KL散度=交叉熵。
代码的话,就是用nn.KLDivLoss()(input,target)就好,也就是相对熵损失:通过求散度得到Loss值, 用于衡量两个分布的相似性,越小越相似。
KD训练代码
导入包
import math
import torch
import torch.nn as nn
import torch.nn.functional as F
from torchvision import datasets, transforms
import torch.utils.data
torch.manual_seed(0)
torch.cuda.manual_seed(0) #设置GPU生成随机数的种子,方便下次复现实验结果。
网络架构
teacher网络
class TeacherNet(nn.Module): #继承Module
def __init__(self):
super(TeacherNet, self).__init__()
self.conv1 = nn.Conv2d(1, 32, 3, 1)
self.conv2 = nn.Conv2d(32, 64, 3, 1)
self.dropout1 = nn.Dropout2d(0.3)
self.dropout2 = nn.Dropout2d(0.5)
self.fc1 = nn.Linear(9216, 128)
self.fc2 = nn.Linear(128, 10)
def forward(self, x):
x = self.conv1(x)
x = F.relu(x)
x = self.conv2(x)
x = F.relu(x)
x = F.max_pool2d(x, 2)
x = self.dropout1(x)
x = torch.flatten(x, 1)
x = self.fc1(x)
x = F.relu(x)
x = self.dropout2(x)
output = self.fc2(x)
return output
student网络
class StudentNet(nn.Module):
def __init__(self):
super(StudentNet, self).__init__()
self.fc1 = nn.Linear(28 * 28, 128)
self.fc2 = nn.Linear(128, 64)
self.fc3 = nn.Linear(64, 10)
def forward(self, x):
x = torch.flatten(x, 1)
x = F.relu(self.fc1(x))
x = F.relu(self.fc2(x))
output = F.relu(self.fc3(x))
return output
teacher网络训练
定义基本函数
def train_teacher(model, device, train_loader, optimizer, epoch):
model.train() #train过程model.train()的作用是启用 Batch Normalization 和 Dropout。model.train()是保证BN层能够用到每一批数据的均值和方差
trained_samples = 0
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device) #放到GPU
optimizer.zero_grad() #归0
output = model(data) #得到结果
loss = F.cross_entropy(output, target) #计算损失 使用交叉熵
loss.backward() #后向传播更新参数
optimizer.step() #优化器调整超参数
trained_samples += len(data)
progress = math.ceil(batch_idx / len(train_loader) * 50)
print("\rTrain epoch %d: %d/%d, [%-51s] %d%%" %
(epoch, trained_samples, len(train_loader.dataset),
'-' * progress + '>', progress * 2), end='')
def test_teacher(model, device, test_loader):
model.eval() #保证BN层能够用全部训练数据的均值和方差
test_loss = 0
correct = 0
with torch.no_grad(): #冻结参数
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data) #模型得到结果
test_loss += F.cross_entropy(output, target, reduction='sum').item() # 统计所有的losssum up batch loss
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability 得到每一行的最大值下标
correct += pred.eq(target.view_as(pred)).sum().item() #eq是一个判断函数 view_as是拉成一列
test_loss /= len(test_loader.dataset) #得到平均loss
print('\nTest: average loss: {:.4f}, accuracy: {}/{} ({:.0f}%)'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
return test_loss, correct / len(test_loader.dataset)
训练主函数
def teacher_main():
epochs = 10
batch_size = 64
torch.manual_seed(0) #设置CPU生成随机数的种子,方便下次复现实验结果。
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data/MNIST', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data/MNIST', train=False, download=True, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=1000, shuffle=True)
model = TeacherNet().to(device) #模型装进GPU中
optimizer = torch.optim.Adadelta(model.parameters()) #定义优化器 其实需要传入模型参数让优化器知道参数空间
'''
optimzier优化器的作用:优化器就是需要根据网络反向传播的梯度信息来
再次更新网络的参数,以起到降低loss函数计算值的作用。
'''
teacher_history = [] #保存历史数据
for epoch in range(1, epochs + 1):
train_teacher(model, device, train_loader, optimizer, epoch)
loss, acc = test_teacher(model, device, test_loader) #相当于验证集作用 也可以绘图
teacher_history.append((loss, acc))
torch.save(model.state_dict(), "teacher.pt")
return model, teacher_history
# 训练教师网络
teacher_model, teacher_history = teacher_main()
student网络训练(重点)
理论部分
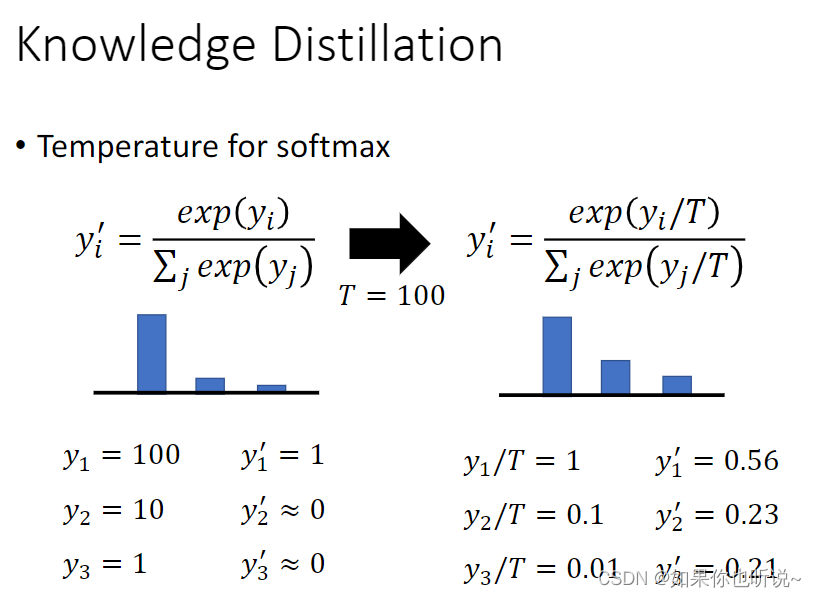
这里的q是经过了softmax之后的分布
student的loss来源于两个部分,Loss将两个loss相加
- studet的HARD Loss是根据one-hot的真实样本p分布得到(和一般的loss一样)
- student的SOFT loss是来源于teacher的分布q’‘(是将q’蒸馏平滑后的结果)
定义kd的loss
# 这里定义的是SOFT Loss + 交叉熵(HARD Loss)
def distillation(y, labels, teacher_scores, temp, alpha):
return nn.KLDivLoss()(F.log_softmax(y / temp, dim=1), F.softmax(teacher_scores / temp, dim=1)) * (
temp * temp * 2.0 * alpha) + F.cross_entropy(y, labels) * (1. - alpha) #两个分布都是T_softmax来求相对熵
可以指定loss function的reduction参数,来设置每个样本loss的最后得到数据loss计算方式;
ℓ ( x , y ) = { L , if reduction = ’none’ mean ( L ) , if reduction = ’mean’ N ∗ mean ( L ) , if reduction = ’batchmean’ sum ( L ) , if reduction = ’sum’ \ell(x, y)=\left\{\begin{array}{ll}L, & \text { if reduction }=\text { 'none' } \\ \operatorname{mean}(L), & \text { if reduction }=\text { 'mean' } \\ N*\operatorname {mean}(L), & \text { if reduction }=\text { 'batchmean' } \\ \operatorname{sum}(L), & \text { if reduction }=\text { 'sum' }\end{array} \right. ℓ(x,y)=⎩ ⎨ ⎧L,mean(L),N∗mean(L),sum(L), if reduction = ’none’ if reduction = ’mean’ if reduction = ’batchmean’ if reduction = ’sum’
定义基本函数
def train_student_kd(model, device, train_loader, optimizer, epoch):
model.train()
trained_samples = 0
for batch_idx, (data, target) in enumerate(train_loader):
data, target = data.to(device), target.to(device)
optimizer.zero_grad()
output = model(data)
teacher_output = teacher_model(data) #得到teacher网络的推断用于后续计算student的loss
teacher_output = teacher_output.detach() # 切断老师网络的反向传播
loss = distillation(output, target, teacher_output, temp=5.0, alpha=0.7)
loss.backward()
optimizer.step()
trained_samples += len(data)
progress = math.ceil(batch_idx / len(train_loader) * 50)
print("\rTrain epoch %d: %d/%d, [%-51s] %d%%" %
(epoch, trained_samples, len(train_loader.dataset),
'-' * progress + '>', progress * 2), end='')
def test_student_kd(model, device, test_loader):
model.eval()
test_loss = 0
correct = 0
with torch.no_grad():
for data, target in test_loader:
data, target = data.to(device), target.to(device)
output = model(data)
test_loss += F.cross_entropy(output, target, reduction='sum').item() # sum up batch loss item()函数可以理解为得到纯粹的数值
pred = output.argmax(dim=1, keepdim=True) # get the index of the max log-probability
correct += pred.eq(target.view_as(pred)).sum().item()
test_loss /= len(test_loader.dataset)
print('\nTest: average loss: {:.4f}, accuracy: {}/{} ({:.0f}%)'.format(
test_loss, correct, len(test_loader.dataset),
100. * correct / len(test_loader.dataset)))
return test_loss, correct / len(test_loader.dataset)
训练主函数
def student_kd_main():
epochs = 10
batch_size = 64
torch.manual_seed(0)
device = torch.device("cuda" if torch.cuda.is_available() else "cpu")
train_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data/MNIST', train=True, download=True,
transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=batch_size, shuffle=True)
test_loader = torch.utils.data.DataLoader(
datasets.MNIST('../data/MNIST', train=False, download=True, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=1000, shuffle=True)
model = StudentNet().to(device)
optimizer = torch.optim.Adadelta(model.parameters())
student_history = []
for epoch in range(1, epochs + 1):
train_student_kd(model, device, train_loader, optimizer, epoch)
loss, acc = test_student_kd(model, device, test_loader)
student_history.append((loss, acc))
torch.save(model.state_dict(), "student_kd.pt")
return model, student_history
student_kd_model, student_kd_history = student_kd_main()
绘制结果
import matplotlib.pyplot as plt
epochs = 10
x = list(range(1, epochs+1))
plt.subplot(2, 1, 1)
plt.plot(x, [teacher_history[i][1] for i in range(epochs)], label='teacher')
plt.plot(x, [student_kd_history[i][1] for i in range(epochs)], label='student with KD')
plt.plot(x, [student_simple_history[i][1] for i in range(epochs)], label='student without KD')
plt.title('Test accuracy')
plt.legend()
plt.subplot(2, 1, 2)
plt.plot(x, [teacher_history[i][0] for i in range(epochs)], label='teacher')
plt.plot(x, [student_kd_history[i][0] for i in range(epochs)], label='student with KD')
plt.plot(x, [student_simple_history[i][0] for i in range(epochs)], label='student without KD')
plt.title('Test loss')
plt.legend()
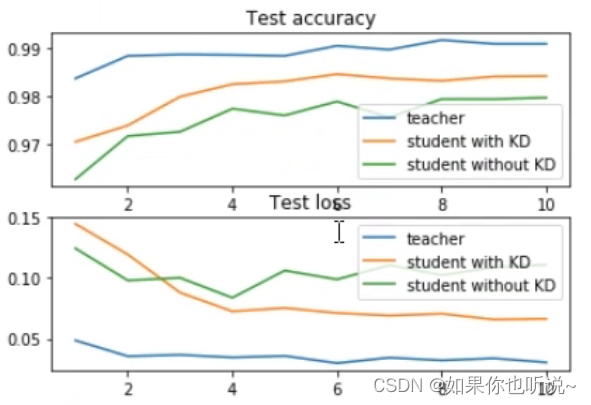
可以看到在teacher的帮助下,student可以学得更好🐱
teacher网络的暗知识
softmax_t
import numpy as np
from matplotlib import pyplot as plt
def softmax_t(x, t):
x_exp = np.exp(x / t)
return x_exp / np.sum(x_exp)
test_loader_bs1 = torch.utils.data.DataLoader(
datasets.MNIST('../data/MNIST', train=False, download=True, transform=transforms.Compose([
transforms.ToTensor(),
transforms.Normalize((0.1307,), (0.3081,))
])),
batch_size=1, shuffle=True)
推断
teacher_model.eval()
with torch.no_grad():
data, target = next(iter(test_loader_bs1))
data, target = data.to('cuda'), target.to('cuda')
output = teacher_model(data)
test_x = data.cpu().numpy() #放进cpu转换成numpy
y_out = output.cpu().numpy()
y_out = y_out[0, ::]
print('Output (NO softmax):', y_out)
plt.subplot(3, 1, 1)
plt.imshow(test_x[0, 0, ::])
plt.subplot(3, 1, 2)
plt.bar(list(range(10)), softmax_t(y_out, 1), width=0.3) #直方图
plt.subplot(3, 1, 3)
plt.bar(list(range(10)), softmax_t(y_out, 10), width=0.3)
plt.show()
Output (NO softmax): [-31.14481 -30.600847 -3.2787514 -20.624037 -31.863455 -37.684086 -35.177486 -22.72263 -16.028662 -26.460657 ]
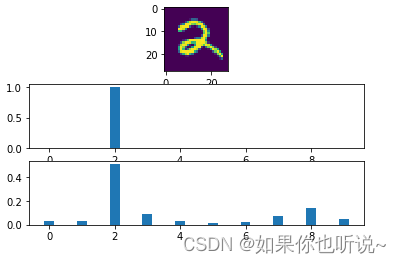
可以看到数据更加平滑,并且可以体现出这个数字不仅是2还和8有些类似⛄️。
本质

在知识蒸馏中,本质上就是使用SOFT Loss来替代正则化项,去拟合teacher的效果。
L2左边是极大似然,右边是先验知识(人为设置)
这里用teacher的知识去正则化作为先验知识,嗯!结束!