数组题目总结 -- 花式遍历

news2024/9/21 8:02:42

目录

  • 一. 反转字符串中的单词
    • 思路和代码：
      • I. 博主的做法
      • II. 东哥的做法
      • III. 其他做法1
      • IV. 其他做法2
  • 二. 旋转图像
    • 思路和代码：
      • I. 博主的做法
      • II. 东哥的做法
  • 三. 旋转图像（逆时针旋转90°）
    • 思路和代码：
      • I. 博主和东哥的做法
  • 四. 矩阵的螺旋遍历
    • 思路和代码：
      • I. 博主的做法
      • II. 东哥的做法
  • 五. 构建螺旋矩阵
    • 思路和代码：
      • I. 博主的做法
      • II. 东哥的做法

一. 反转字符串中的单词

  • 题目链接：https://leetcode.cn/problems/reverse-words-in-a-string/

思路和代码：

I. 博主的做法

  • 先用trim()方法把字符串前后的多余空格全部去掉。
  • 再用replaceAll(“\\s+”, " ")；把多个空格替换成一个空格，\s代表空格，+代表多个。
  • 用split以空格为标志，切分字符串，放到字符串数组中。
  • 之后使用StringBuffer反向存储。
class Solution {
    public String reverseWords(String s) {
        s = s.trim().replaceAll("\\s+", " ");
        String[] temp = s.split(" ");
        StringBuffer stb = new StringBuffer();

        for(int i = temp.length-1; i > 0; i--){
            stb.append(temp[i] + " ");
        }
        stb.append(temp[0]);
        
        return stb.toString();
    }
}
  • 申请了额外的空间，原地反转，博主不会，，，
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

II. 东哥的做法

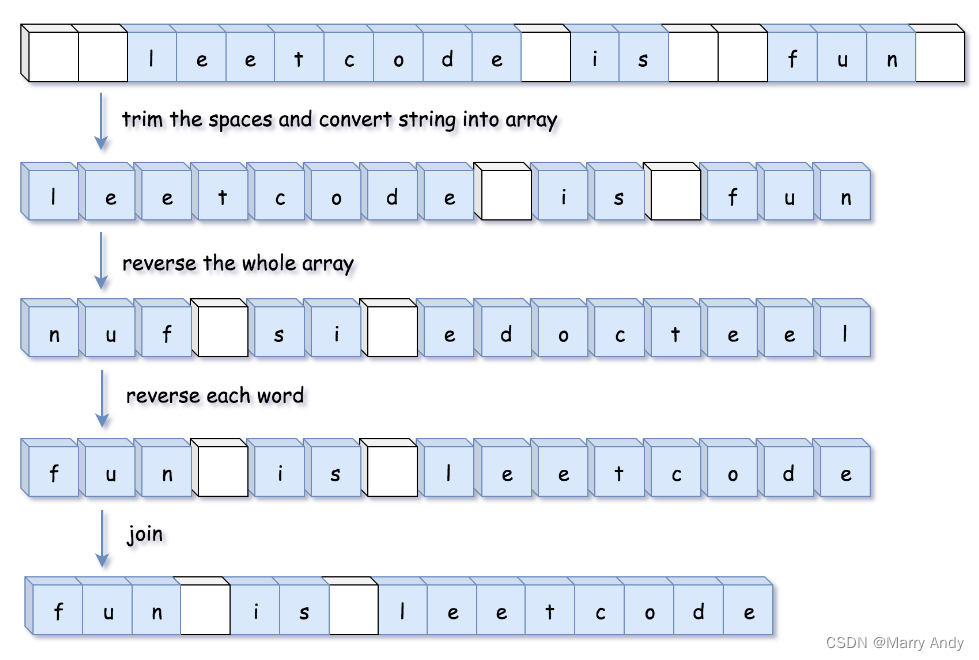
  • 先反转整个字符串。
  • 然后反转每一个单词。
    在这里插入图片描述
class Solution {
    public StringBuilder trimSpace(String s){
        int left = 0, right = s.length()-1;
		//去除开头和结尾的空格
        while(left <= right && s.charAt(left) == ' ')
            left++;
        while(left <= right && s.charAt(right) == ' ')
            right--;
            
		//去除字符串中间的空格
        StringBuilder stb1 = new StringBuilder();
        while(left <= right){

            if(s.charAt(left) != ' ')
                stb1.append(s.charAt(left));
            else if(stb1.charAt(stb1.length()-1) != ' ')
                stb1.append(s.charAt(left));
            
            left++;
        }
        return stb1;
    }
    
    //写的挺巧妙的反转函数，可以积累
    public void reverse(StringBuilder stb, int left, int right){
        while (left < right) {
            char temp = stb.charAt(left);
            stb.setCharAt(left++, stb.charAt(right));   
            stb.setCharAt(right--, temp);
        }

    }
    public void reverseWord(StringBuilder stb){
        int start = 0, end = 0;

        while(start < stb.length()){
            while(end < stb.length() && stb.charAt(end) != ' ')
                end++;
            
            reverse(stb, start, end-1);
            //寻找下一个单词
            start = end + 1;
            end++;
        } 

    }
    
    //总函数
    public String reverseWords(String s) {

        StringBuilder stb = trimSpace(s);
        
		//StringBuilder 不用再加返回值，直接就在原地操作了
        reverse(stb, 0, stb.length()-1);

        reverseWord(stb);

        return stb.toString();
    }
}
  • StringBuilder一定要定义在循环外面，循环里面的属于临时变量，外面的函数是调用不了的。
  • 如果是StringBuilder，就不用再有返回值，因为StringBuilder是可变的，而java中String是不可变的，需要额外申请空间进行操作。C++中，String是可变的，所以空间复杂度能降到O(1)，不需要额外申请空间。
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

III. 其他做法1

  • 去除开头和末尾的空格。
  • 运用正则表达式将字符串分成一个一个的单词（用一个或者多个空格当做分隔符），返回的数组转换成List。
  • 反转List，相当于将单词的顺序做一个反转。
  • 将空格加入到List当中。
class Solution {
    public String reverseWords(String s) {
        // 除去开头和末尾的空白字符
        s = s.trim();
        // 正则匹配连续的空白字符作为分隔符分割
        List<String> wordList = Arrays.asList(s.split("\\s+"));
        Collections.reverse(wordList);
        return String.join(" ", wordList);
    }
}
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

IV. 其他做法2

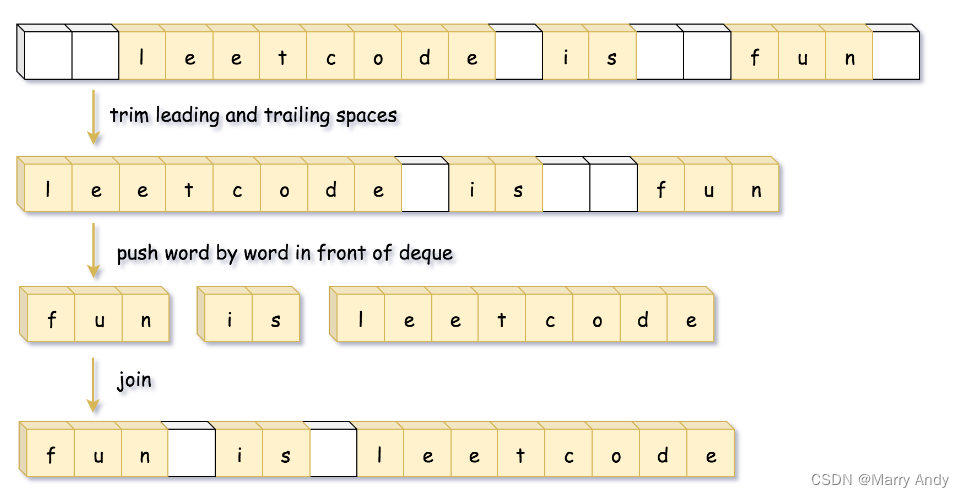
  • 去掉头尾两头的空格
  • 将字符串加入双端队列的头部或者直接加入栈中，如下图：
    在这里插入图片描述
class Solution {
    public String reverseWords(String s) {
        int left = 0, right = s.length()-1;
		//去掉前后两头的空格
        while(left <= right && s.charAt(left) == ' ')
            left++;
        while(left <= right && s.charAt(right) == ' ')
            right--;
        //使用双端队列存字符串，使用StringBuilder来存单词
        Deque<String> deque = new ArrayDeque<>();
        StringBuilder stb = new StringBuilder();

        while(left <= right){
        	//如果StringBuilder中不为空（单词存在），并且遇到下一个空格了，就从头部加入双端队列并清空StringBuilder
            if(stb.length() != 0 && s.charAt(left) == ' '){
                deque.offerFirst(stb.toString());
                stb.setLength(0);
            }
            else if(s.charAt(left) != ' ')
                stb.append(s.charAt(left));

            left++;
        }
        //记得加入最后一个单词，因为遇不到下一个空格了！！！   
        deque.offerFirst(stb.toString());
		
        return String.join(" ", deque);
    }
}
  • 时间复杂度：O(n)
  • 空间复杂度：O(n)

二. 旋转图像

  • 题目链接：https://leetcode.cn/problems/rotate-image/

思路和代码：

I. 博主的做法

  • 博主只能想到一圈一圈的进行迭代数组。。。太复杂了。

II. 东哥的做法

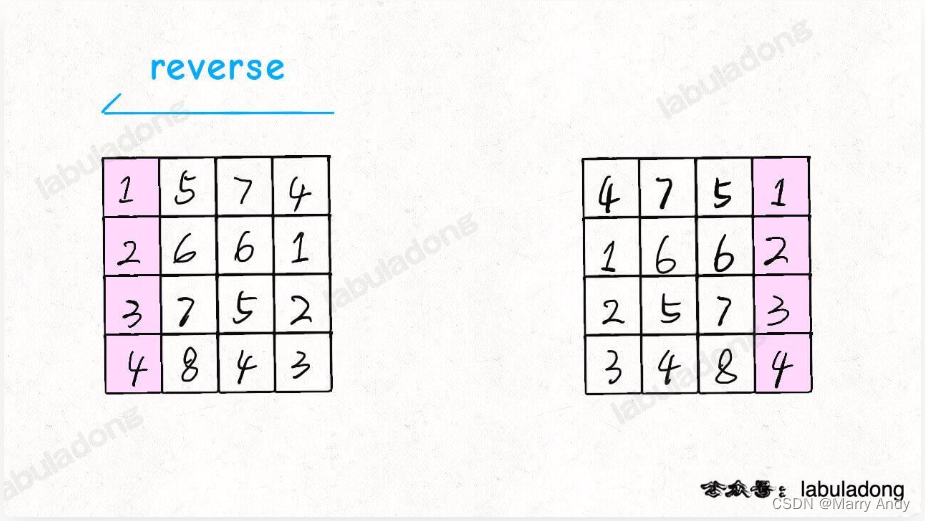
  • 先将矩阵沿对角线，做对称矩阵操作

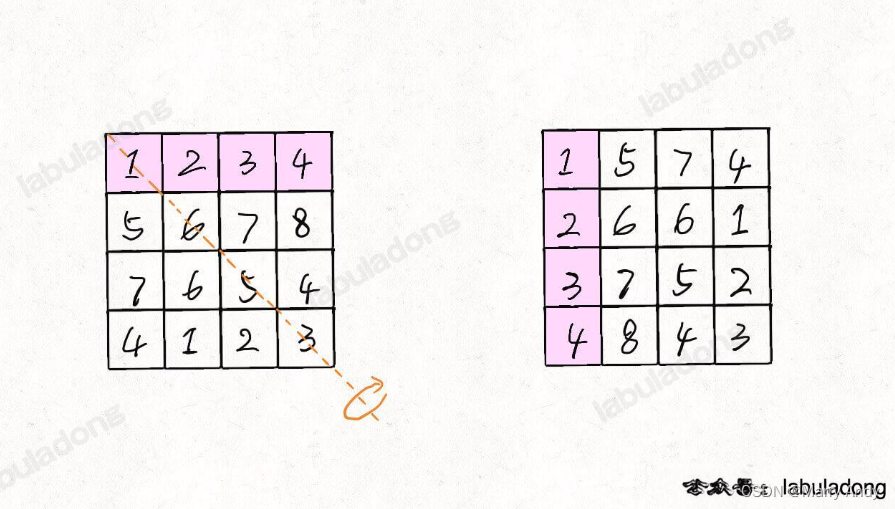
在这里插入图片描述

  • 对矩阵的每一行进行反转
    在这里插入图片描述
    在这里插入图片描述
class Solution {
	//以对角线对称交换矩阵
    public void symmetry(int[][] matrix){
        for(int i = 0; i < matrix.length; i++)
            for(int j = 0; j < i; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[j][i];
                matrix[j][i] = temp;
            }
    }
    
    //将每一行进行反转
    public void reverse(int[] num){
        int left = 0, right = num.length-1;
        while(left <= right){
            int temp = num[left];
            num[left++] = num[right];
            num[right--] = temp;
        }

    }
    public void rotate(int[][] matrix) {
        symmetry(matrix);

        for(int[] n : matrix)
            reverse(n);
             
    }
}
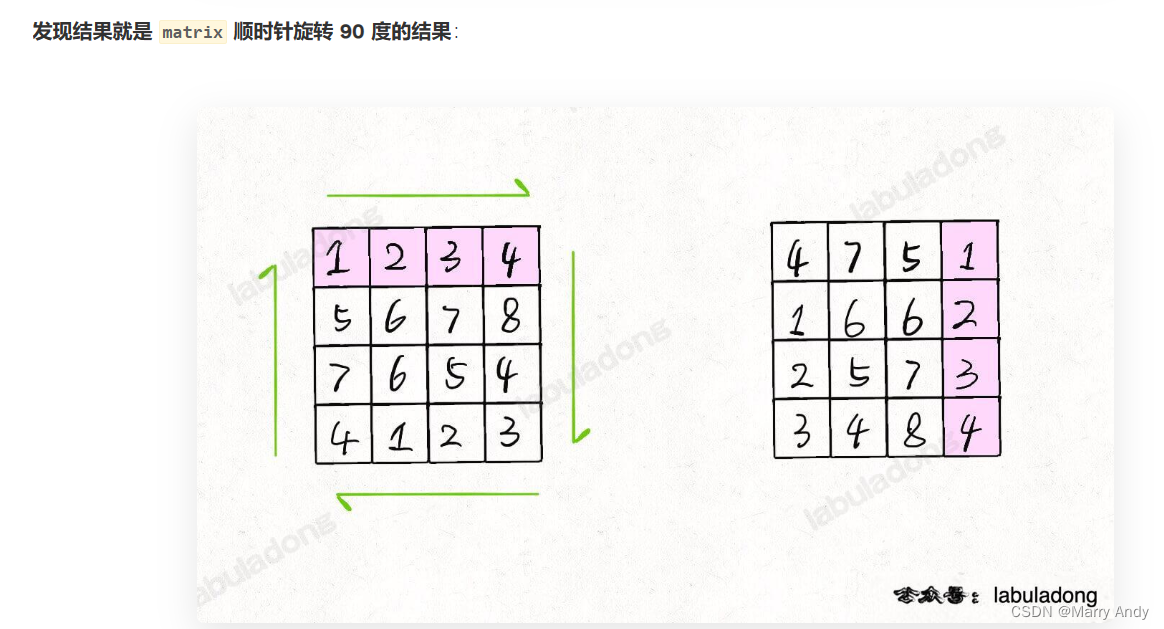
  • 常规的思路就是去寻找原始坐标和旋转后坐标的映射规律，但我们是否可以让思维跳跃跳跃，尝试把矩阵进行反转、镜像对称等操作，可能会出现新的突破口。
  • 仔细想想，旋转二维矩阵的难点在于将「行」变成「列」，将「列」变成「行」，而只有按照对角线的对称操作是可以轻松完成这一点的，对称操作之后就很容易发现规律了。

三. 旋转图像（逆时针旋转90°）

  • 题目链接：无。
  • 函数名： public void rotate(int[][] matrix){ }

思路和代码：

I. 博主和东哥的做法

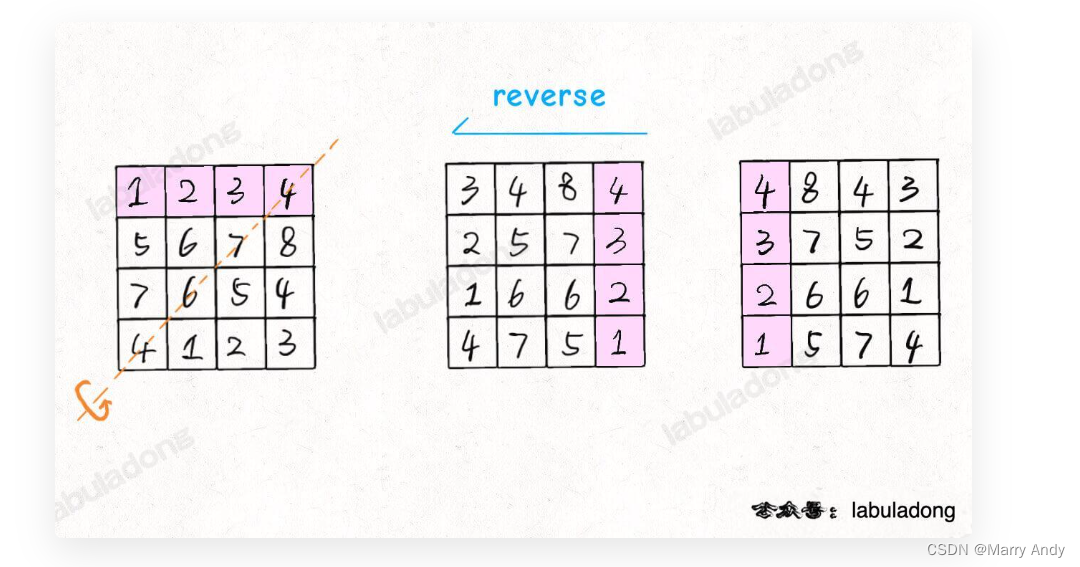
  • 和上一道题真的很像，就是沿着另一条对角线旋转，然后反转每一行。
    在这里插入图片描述
package 洛谷;

import java.util.Scanner;

public class Test {
	//沿逆对角线进行对称
    public static void romate(int[][] matrix){
        for(int i = 0; i < matrix.length; i++)
            for(int j = 0; j < matrix.length-i; j++){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[matrix.length - 1 - j][matrix.length - 1 - i];
                matrix[matrix.length - 1 - j][matrix.length - 1 - i] = temp;
            }
    }

	//每行进行反转
    public static void reverse(int[] matrix){
        int left = 0, right = matrix.length-1;

        while(left <= right){
            int temp = matrix[left];
            matrix[left++] = matrix[right];
            matrix[right--] = temp;
        }
    }
    
    //主函数
    public static void main(String[] args){
        Scanner sc = new Scanner(System.in);
        int[][] a = {{1,2,3,4}, {5,6,7,8}, {7,6,5,4},{4,1,2,3}};

        romate(a);

        for(int[] num : a)
            reverse(num);

        for(int i = 0; i < a.length; i++){
            for(int j = 0; j < a.length; j++)
                System.out.print(a[i][j] + " ");
            System.out.println();
        }

    }

}
  • 顺逆对角线对称的逻辑还是不太会，仍需加强

四. 矩阵的螺旋遍历

  • 题目链接：https://leetcode.cn/problems/spiral-matrix/

思路和代码：

I. 博主的做法

  • 设置4个边界，然后模拟顺序输出的样子，进行遍历
class Solution {
    public List<Integer> spiralOrder(int[][] matrix) {
        int top = 0, left = 0, right = matrix[0].length-1, bottom = matrix.length-1;
        
        List<Integer> list = new ArrayList<>();

        while(left <= right && top <= bottom){
            for(int j = left; top <= bottom && j <= right; j++)
                list.add(matrix[top][j]);
            top++;

            for(int i = top; left <= right && i <= bottom; i++)
                list.add(matrix[i][right]);
            right--;

            for(int j = right; top <= bottom && j >= left; j--)
                list.add(matrix[bottom][j]);
            bottom--;

            for(int i = bottom; left <= right && i >= top; i--)
                list.add(matrix[i][left]);
            left++;
        }

        return list;
    }
}
  • 这一行写成：for(int j = left; left <= right && j <= right; j++)，这显然是错的，j <= right已经判断过了；其次，如果上下都是负的空间，左右又有什么意义呢？？
  • 还需要注意，螺旋输出，没拐个弯，对应的边界就要多走一格子。
  • 列的个数一定是matrix[0].length - 1，行的个数是matrix.length

II. 东哥的做法

  • 和博主想的一样，设置四个边界
List<Integer> spiralOrder(int[][] matrix) {
    int m = matrix.length, n = matrix[0].length;
    int upper_bound = 0, lower_bound = m - 1;
    int left_bound = 0, right_bound = n - 1;
    List<Integer> res = new LinkedList<>();
    // res.size() == m * n 则遍历完整个数组
    while (res.size() < m * n) {
        if (upper_bound <= lower_bound) {
            // 在顶部从左向右遍历
            for (int j = left_bound; j <= right_bound; j++) {
                res.add(matrix[upper_bound][j]);
            }
            // 上边界下移
            upper_bound++;
        }
        
        if (left_bound <= right_bound) {
            // 在右侧从上向下遍历
            for (int i = upper_bound; i <= lower_bound; i++) {
                res.add(matrix[i][right_bound]);
            }
            // 右边界左移
            right_bound--;
        }
        
        if (upper_bound <= lower_bound) {
            // 在底部从右向左遍历
            for (int j = right_bound; j >= left_bound; j--) {
                res.add(matrix[lower_bound][j]);
            }
            // 下边界上移
            lower_bound--;
        }
        
        if (left_bound <= right_bound) {
            // 在左侧从下向上遍历
            for (int i = lower_bound; i >= upper_bound; i--) {
                res.add(matrix[i][left_bound]);
            }
            // 左边界右移
            left_bound++;
        }
    }
    return res;
}
  • 思路是一样的，大家看着哪个顺眼参考哪个

五. 构建螺旋矩阵

  • 题目链接：https://leetcode.cn/problems/spiral-matrix-ii/

思路和代码：

I. 博主的做法

  • 跟上个题几乎是一模一样，只是在每次循环当中进行的操作不同而已。
class Solution {
    public int[][] generateMatrix(int n) {
        int[][] matrix = new int[n][n];

        int top = 0, left = 0, right = n-1, bottom = n-1;
        int num = 1;

        while(top <= bottom && left <= right){
            for(int j = left; top <= bottom && j <= right; j++)
            	//这里不一样，下面同理
                matrix[top][j] = num++;
            top++;

            for(int i = top; left <= right && i <= bottom; i++)
                matrix[i][right] = num++;
            right--;

            for(int j = right; top <= bottom && j >= left; j--)
                matrix[bottom][j] = num++;
            bottom--;

            for(int i = bottom; left <= right && i >= top; i--)
                matrix[i][left] = num++;
            left++;
        }

        return matrix;
    }
}
  • 时间复杂度：O(n^2)，其中 n 是给定的正整数。矩阵的大小是 n×n，需要填入矩阵中的每个元素。
  • 空间复杂度：O(1)，除了返回的矩阵以外，空间复杂度是常数。

II. 东哥的做法

  • 和博主想的一样，设置四个边界
int[][] generateMatrix(int n) {
    int[][] matrix = new int[n][n];
    int upper_bound = 0, lower_bound = n - 1;
    int left_bound = 0, right_bound = n - 1;
    // 需要填入矩阵的数字
    int num = 1;
    
    while (num <= n * n) {
        if (upper_bound <= lower_bound) {
            // 在顶部从左向右遍历
            for (int j = left_bound; j <= right_bound; j++) {
                matrix[upper_bound][j] = num++;
            }
            // 上边界下移
            upper_bound++;
        }
        
        if (left_bound <= right_bound) {
            // 在右侧从上向下遍历
            for (int i = upper_bound; i <= lower_bound; i++) {
                matrix[i][right_bound] = num++;
            }
            // 右边界左移
            right_bound--;
        }
        
        if (upper_bound <= lower_bound) {
            // 在底部从右向左遍历
            for (int j = right_bound; j >= left_bound; j--) {
                matrix[lower_bound][j] = num++;
            }
            // 下边界上移
            lower_bound--;
        }
        
        if (left_bound <= right_bound) {
            // 在左侧从下向上遍历
            for (int i = lower_bound; i >= upper_bound; i--) {
                matrix[i][left_bound] = num++;
            }
            // 左边界右移
            left_bound++;
        }
    }
    return matrix;
}

参考：
https://labuladong.github.io/algo/di-yi-zhan-da78c/shou-ba-sh-48c1d/er-wei-shu-150fb/
https://leetcode.cn/problems/reverse-words-in-a-string/solution/fan-zhuan-zi-fu-chuan-li-de-dan-ci-by-leetcode-sol/

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/564858.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

SpringBoot2-基础入门（一）

SpringBoot2-基础入门（一）

SpringBoot2-基础入门&#xff08;一&#xff09; 文章目录 SpringBoot2-基础入门&#xff08;一&#xff09;1. 为什么学习SpringBoot1.1 SpringBoot的优点1.2 SpringBoot的缺点1.3 SpringBoot开发环境 2. 第一个SpringBoot程序2.1 添加依赖2.2 编写主程序类 -- 固定写法2.3 编…
阅读更多...
SpringCloud（25）：熔断降级实现

SpringCloud（25）：熔断降级实现

熔断降级会在调用链路中某个资源出现不稳定状态时&#xff08;例如调用超时或异常比例升高&#xff09;&#xff0c;对这个资源的调用进行限制&#xff0c;让请求快速失败&#xff0c;避免影响到其它的资源而导致级联错误。当资源被降级后&#xff0c;在接下来的降级时间窗口之…
阅读更多...
硅谷新王登国会山，呼吁加强 AI 监管；马斯克任命推特新 CEO；数字媒体巨头申请破产；欧盟通过全球首个全面监管加密资产框架 | 经济学人第 21 周

硅谷新王登国会山，呼吁加强 AI 监管；马斯克任命推特新 CEO；数字媒体巨头申请破产；欧盟通过全球首个全面监管加密资产框架 | 经济学人第 21 周

1. 硅谷新王登国会山&#xff0c;呼吁加强 AI 监管 Sam Altman, the chief executive of OpenAI, the firm behind the ChatGPT chatbot, called for tighter regulation of rapidly developing generative artificial intelligence, such as by forcing disclosure on images …
阅读更多...
【文件操作与IO】

【文件操作与IO】

目录 一、文件 1、文件的定义 2、File类 &#x1f345;File类中的常见属性 &#x1f345;File类中的构造方法 &#x1f345;File类中的常用方法 二、文件内容的读取-数据流 &#x1f345;InputStream概述 &#x1f345;FileInputStream &#x1f345;OutputStream 概…
阅读更多...
真题详解（汇总）-软件设计（八十三)

真题详解（汇总）-软件设计（八十三)

真题详解&#xff08;include&#xff09;-软件设计&#xff08;八十二)https://blog.csdn.net/ke1ying/article/details/130828203 软件交付后进入维护阶段&#xff0c;采用专门的程序模块对文件或者数据中记录进行增加、删除和修改操作&#xff0c;属于&#xff1f; 解析&a…
阅读更多...
Netty重试一定次数后调用System.exit(n)退出应用程序(二)

Netty重试一定次数后调用System.exit(n)退出应用程序(二)

System.exit()方法 原型&#xff1a;System.exit(int status) 其功能主要是调用Runtime.getRuntime().exit(status); 作用是终止当前正在运行的Java虚拟机&#xff0c;这个status表示退出的状态码&#xff0c;非零表示异常终止。(可以返回给其他进程的调用者一个调用的返回码…
阅读更多...
RES 新的数据集 Advancing Referring Expression Segmentation Beyond Single Image 论文笔记

RES 新的数据集 Advancing Referring Expression Segmentation Beyond Single Image 论文笔记

RES 新的数据集 Advancing Referring Expression Segmentation Beyond Single Image 论文笔记 一、Abstract二、引言三、相关工作3.1 Referring Expression Segmentation (RES)3.2 CoSalient Object Detection (CoSOD) 四、提出的方法4.1 概述文本 & 图像编码器TQM & H…
阅读更多...
OpenStreetMap实战

OpenStreetMap实战

介绍 OpenStreetMap&#xff08;OSM&#xff09;是一个由志愿者创建并维护的免费和开源的地图数据库。其目的是为全球任何人提供可自由使用、编辑和分发的地图数据。OpenStreetMap数据库中的地理要素包括道路、建筑、河流、森林、山脉、公共设施等。由于OpenStreetMap是开放的…
阅读更多...
数据结构初阶 —— 二叉树链式结构

数据结构初阶 —— 二叉树链式结构

目录 一&#xff0c;二叉树链式结构 二&#xff0c;二叉树的遍历&#xff08;四种&#xff09; 前序遍历 中序遍历 后序遍历 层序遍历 三&#xff0c;二叉树接口 四&#xff0c;试题 一&#xff0c;二叉树链式结构 普通二叉树的增删查改&#xff0c;意义不大&#xff1b…
阅读更多...
JavaScript基础扫盲

JavaScript基础扫盲

博主简介&#xff1a;想进大厂的打工人博主主页&#xff1a;xyk:所属专栏: JavaEE初阶 本篇文章为大家带来JavaScript的学习&#xff0c;一图胜千言~~~ 目录 文章目录 1.1 JavaScript (简称 JS) 1.2 JavaScript发展历史 1.3 JavaScript运行过程 二、JavaScript的基础语法 2.1 …
阅读更多...
Linux内核源码分析-进程调度(五)-组调度

Linux内核源码分析-进程调度(五)-组调度

出现的背景 总结来说是希望不同分组的任务在高负载下能分配可控比例的CPU资源。为什么会有这个需求呢&#xff0c;假设多用户计算机系统每个用户的所有任务划分到一个分组中&#xff0c;A用户90个任务&#xff0c;而B用户只有10个任务&#xff08;这100个任务假设都是优先级一…
阅读更多...
物联网手势控制小车所遇问题与解决方案

物联网手势控制小车所遇问题与解决方案

LCD1602无法显示问题 问题描述&#xff1a;按照开源社区教程完成LCD1602驱动显示程序的编写&#xff0c;成功点亮屏幕&#xff0c;开启背光&#xff0c;但无法观察到显示数据。 分析过程与解决方案&#xff1a; 1.是否IIC地址不对 使用以下代码扫描IIC总线上的设备&#xf…
阅读更多...
Go学习圣经：队列削峰+批量写入 超高并发原理和实操

Go学习圣经：队列削峰+批量写入 超高并发原理和实操

说在前面&#xff1a; 本文是《Go学习圣经》 的第二部分。 第一部分请参见&#xff1a;Go学习圣经&#xff1a;0基础精通GO开发与高并发架构&#xff08;1&#xff09; 现在拿到offer超级难&#xff0c;甚至连面试电话&#xff0c;一个都搞不到。 尼恩的技术社群中&#xf…
阅读更多...
K近邻算法实现红酒数据集分类

K近邻算法实现红酒数据集分类

目录 1. 作者介绍2. K近邻算法介绍2.1 K基本原理2.2 算法优缺点 3. KNN红酒数据集分类实验3.1 获取红酒数据集3.2 KNN算法3.3 完整代码 4. 问题分析参考链接&#xff08;可供参考的链接和引用文献&#xff09; 1. 作者介绍 路治东&#xff0c;男&#xff0c;西安工程大学电子信…
阅读更多...
面试问题汇总

面试问题汇总

最近面试了几家公司&#xff0c;对问到的问题汇总一下。 Unity 是左手坐标系还是右手坐标系? 这个题靠记忆答的答错了&#xff0c;是左手坐标系。 大拇指指的方向是X轴&#xff0c;食指指的方向是Y轴方向&#xff0c;中指指的方向Z轴方向。 场景中游戏物体Activity为false,G…
阅读更多...
C语言字符串函数和内存函数的介绍与模拟实现

C语言字符串函数和内存函数的介绍与模拟实现

0.前言 C语言中对字符和字符串的处理很是频繁&#xff0c;但是C语言本身是没有字符串类型的&#xff0c;字符串通常放在 常量字符串 中或者 字符数组 中。 字符串常量 适用于那些对它不做修改的字符串函数. 1.字符串函数介绍与模拟实现 C语言本身就带有一些库函数&#xff0c;所…
阅读更多...
研发工程师玩转Kubernetes——CPU配额

研发工程师玩转Kubernetes——CPU配额

在一个Pod中&#xff0c;可以有多个容器&#xff0c;比如一个主要业务容器和若干辅助业务容器。如果辅助业务容器内程序有问题&#xff0c;导致占用了大量的CPU资源&#xff0c;进而影响了主要业务容器的执行效率&#xff0c;那就需要进行干涉了。本节我们将使用“资源配额”来…
阅读更多...
Edgedetect

Edgedetect

边缘检测&#xff0c;检测上升沿 对于 8 位矢量中的每个位&#xff0c;检测输入信号何时从一个时钟周期中的 0 变为下一个时钟周期的 1&#xff08;类似于正边沿检测&#xff09;。输出位应在发生 0 到 1 转换后设置周期。 以下是一些示例。为清楚起见&#xff0c;in[1] 和 pe…
阅读更多...
Jenkins+GitLab+Docker搭建前端自动化构建镜像容器部署(无本地证书，映射版本)

Jenkins+GitLab+Docker搭建前端自动化构建镜像容器部署(无本地证书，映射版本)

前言 &#x1f680; 需提前安装环境及知识点&#xff1a; 1、Docker搭建及基础操作 2、DockerFile文件描述 3、Jenkins搭建及基础点 &#x1f680; 目的&#xff1a; 将我们的前端项目打包成一个镜像容器并自动发布部署&#xff0c;可供随时pull访问 一、手动部署镜像及容器 1…
阅读更多...
【Linux】线程分离 | 线程库 | C++调用线程 | 线程局部存储

【Linux】线程分离 | 线程库 | C++调用线程 | 线程局部存储

文章目录 1. 线程分离1. 为什么要线程分离&#xff1f;2. 具体使用3. 为什么有时候分离在调用join 会正常运行&#xff1f; 2. 如何理解线程库&#xff1f;如何理解 先描述 在组织&#xff1f; 3. C中使用多线程4. 线程局部存储局部变量全局变量 1. 线程分离 1. 为什么要线程分…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023