RPG游戏辅助想要做到自动打怪
获得到最近怪物信息以后 还需要面向怪物
否则背对怪物等等情况是没有办法攻击以及释放技能的
游戏设计的时候朝向是有很多种情况的
第一种
2D,2.5D老游戏,例如传奇
他的朝向一般是极为固定的4朝向或则8朝向
也就是不是自由朝向的,只能朝向 东南西北4个方位
或则 东 东北 北 西北 西 西南 南 东南 8个方位
那么朝向计算也极为简单
只要计算出怪物和人物坐标的关系即可
例如
X怪物>X人物 && Y怪物>Y人物
那么想面向怪物就把朝向值修改成面向东北方即可
一般 8个方位是0-7 8个数值表示
第二种
2D版自由朝向
说是2D版自由朝向,但实际上很多3D游戏都在运用
非常简单的理解就是游戏是3D的,但是人物转向只能2D平面转向,而头不可以上抬和俯瞰的
例如QQ西游
一般情况这种游戏的朝向值得是从0到一个数值均匀排列在坐标系上
我们只要计算出他的变化规律 即可轻松计算
例如QQ西游是从 X正轴为0 逆时针不断增加
一直增加到256然后和X轴重叠又变为0
那么知道了 其变化规律 我们就可以代码实现
如下
DWORD Call_朝向怪物角度(FLOAT x,FLOAT y)
{
T人物属性 A;
A.c初始化();
FLOAT X=A.fX;
FLOAT Y=A.fY;
DWORD B=0;
if (x>X&&y>Y)//第一象限
{
B=(DWORD)(atan2(y-Y,x-X)/3.1415926 *180);//真实角度
B=B*64/90 ;//同比例游戏角度
B=0+B;
}
if (x<X&&y>Y)//第二象限
{
B=(DWORD)(atan2(y-Y,X-x)/3.1415926 *180);
B=B*64/90 ;
B=128-B;
}
if (x<X&&y<Y)//第三象限
{
B=(DWORD)(atan2(Y-y,X-x)/3.1415926 *180);
B=B*64/90;
B=128+B;
}
if (x>X&&y<Y)//第四象限
{
B=(DWORD)(atan2(Y-y,x-X)/3.1415926 *180);
B=B*64/90;
B=256-B;
}
return B;
}
第三种
通过第一种和第二种
我们可以明显感觉到从8方位到多方位的升级
但是这还是不够的 无论你把坐标系分成多少份 还是不是绝对的自由
那怎么办呢?
游戏发明出更自由的朝向方式
例如 天涯明月刀
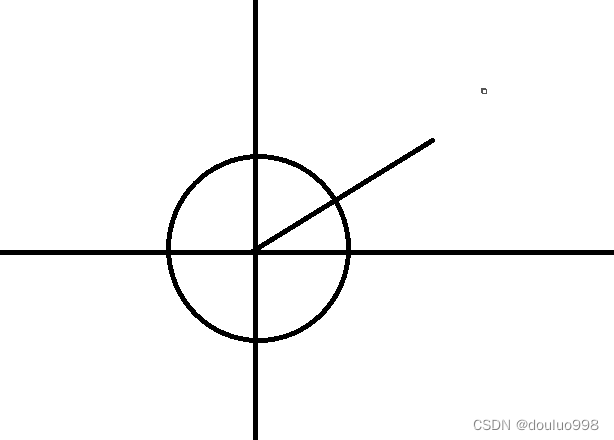
他是这样的设计理念
以人物为中心 花一个圆,一般半径为1(是多少无所谓,我们乘多少即可)
和怪物连线,于圆的交点就是我们的朝向
那么这样就变成了自由朝向了,想精确到多少都可以
计算起来也非常简单
以人物原点,圆交点,圆交点到X轴的垂线和X轴的交点 三点为一个三角形
人物原点,怪物坐标点,怪物坐标点到X轴的垂线和X轴的交点 三点为一个三角形
2个三角形为相似三角形
那么 小三角形h / 1 = (Y怪物-Y人物)/距离
小三角形l / 1 = (X怪物-X人物)/距离
得到的 h 和l 就是我们 圆交点的坐标了
还有进一步的升华的方式
就是3D版本的朝向
那么他将不再是一个圈了
是一个3D立体的球
但是算法依然没有变化
只是距离发生了变化
相似三角形依然还是相似三角形
h=(Y怪物-Y人物)/距离
l=(X怪物-X人物)/距离
z=(Z怪物-Z人物)/距离
其中距离=sqrt((人物.fX-fX)(人物.fX-.fX)+(人物.fY-fY)(人物.fY-fY)+(人物.fZ-fZ)*(人物.fZ-fZ));
第四种
一般是FPS类游戏喜欢用的
也和航天飞机等用的角度一样
就是俯冲角 摇摆角 和旋转角
其中旋转角代表着自身的旋转 ,在游戏里几乎无用
那么就是俯冲角 代表着枪支方向和水平面上下的角度
摇摆角 代表枪支方向和中线左右摇摆的角度
计算方法 参考第二种的反正切方式即可