---

我的思路：依次计算每一列能接收的雨水量。
 

关键点：如何计算得到每一列所能接收到的雨水量？

        某一列能够接收到的雨水量，取决于其左右两侧最高的柱子。仅有当左右两侧的柱子均高于该列的高度，该列才可收到雨水，其雨水量为 min( left_height-h , right_height-h) 。

class Solution:
    def trap(self, height: List[int]) -> int:
        
        # height数组->对象属性
        self.height=height
        self.height_len=len(height)

        # 哈希表存储上一时刻的left_height与right_height
        Hash=dict()
        Hash['left_height']=0
        Hash['right_height']=max(height)
        self.Hash=Hash

        # rain_sum:总雨水量
        rain_sum=0

        # 依次计算每一个柱子所能接水的高度
        # i为索引
        for i in range(len(height)):
            # 传入柱子的索引
            rain_sum+=self.rain_calculate(i)
        return rain_sum
    
    def rain_calculate(self,index):

        # 取自身高度h
        h=self.height[index]

        # 左侧高度
        if index:
            left_height=max(self.Hash['left_height'],self.height[index-1])
        else:
            left_height=0

        # 右侧高度
        if self.height[index]!=self.Hash['right_height']:
            right_height=self.Hash['right_height']

        else:
            if index==self.height_len-1:
                right_height=0
            else:
                seq_temp=self.height[index+1:self.height_len]
                right_height=max(seq_temp)
        
        # 更新哈希表
        self.Hash['left_height']=left_height
        self.Hash['right_height']=right_height
        
        # 仅有当left_height和right_height均高于h时，该列才可接收到雨水
        if left_height>h and right_height>h:
            return min(left_height-h,right_height-h)
        
        else:
            return 0

    

关键点：哈希表存储上一时刻的left_height与right_height

为什么需要存储上一时刻的left_height与right_height？

        数组从左往右遍历，新柱子的 left_height 直接取 max(前一个柱子的left_height , 前一个柱子的高度)，有些类似递归的思想。

        新柱子的 right_height 则分为两种情况，一种是 新柱子的高度不等于前一个柱子的 right_height，这种情况下则令新柱子的 right_height 直接取 前一个柱子的 right_height 即可；另一种情况则是 新柱子的高度等于前一个柱子的 right_height，即说明前一个柱子的 right_height 可能取自该根柱子，则新柱子的 right_height 取后面的柱子的最大值（数组切片） 即可。

---

思路2：动态规划

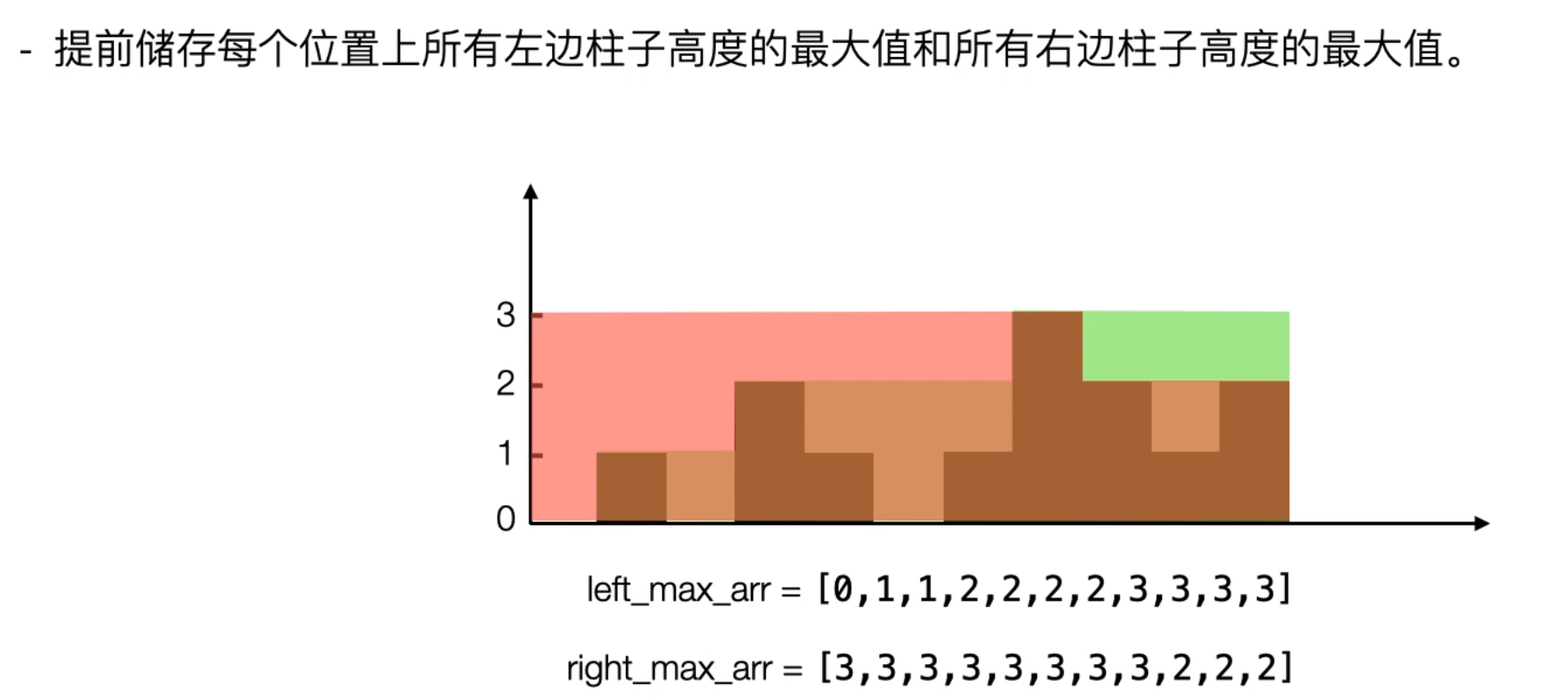
动态规划 - 复杂度分析

时间复杂度为：O(n)

空间复杂度为：O(n)

---

思路3：单调栈

class Solution:
    def trap(self, height: List[int]) -> int:

        ans = 0
        
        # 建立单调递减栈，用列表存储
        stack = list()
        
        # 从左向右依次遍历
        for i, h in enumerate(height):

            # 当栈不为空且h大于栈顶的高度时，进入while循环
            while stack and h > height[stack[-1]]:
                
                # 取出栈顶元素，作为低洼
                top = stack.pop()
                
                # 若取出栈顶元素后栈为空，则跳出while循环
                if not stack:
                    break
                
                # left为左边界的索引，i为右边界的索引
                left = stack[-1]
                currWidth = i - left - 1
                currHeight = min(height[left], height[i]) - height[top]
                ans += currWidth * currHeight
            
            # 循环结束后，将i加入栈中
            stack.append(i)
        
        return ans

关键点：单调递减栈

        考虑到低洼（可接雨水）必须有左右两侧边界，所以用python列表建立单调递减栈。当出现某一根柱子大于栈顶元素的高度时，开始进入内循环。出栈的top为低洼，根据left和right边界索引计算雨水存量，直到下一个栈顶大于等于h，方可跳出内循环。最后一定要将 i 入栈，因为 i 仍可能可以构成某一个低洼的左边界。