【1377. T 秒后青蛙的位置】

news2024/9/22 17:33:27

来源：力扣（LeetCode）

描述：

给你一棵由 n 个顶点组成的无向树，顶点编号从 1 到 n。青蛙从 顶点 1 开始起跳。规则如下：

在一秒内，青蛙从它所在的当前顶点跳到另一个 未访问 过的顶点（如果它们直接相连）。
青蛙无法跳回已经访问过的顶点。
如果青蛙可以跳到多个不同顶点，那么它跳到其中任意一个顶点上的机率都相同。
如果青蛙不能跳到任何未访问过的顶点上，那么它每次跳跃都会停留在原地。

无向树的边用数组 edges 描述，其中 edges[i] = [ai, bi] 意味着存在一条直接连通 ai 和 bi 两个顶点的边。

返回青蛙在 t 秒后位于目标顶点 target 上的概率。与实际答案相差不超过 10^-5 的结果将被视为正确答案。

示例 1：

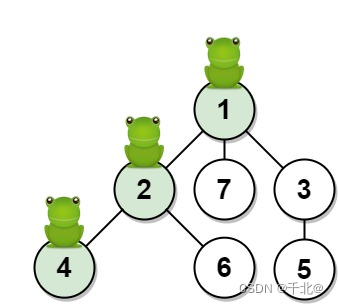
输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 2, target = 4
输出：0.16666666666666666 
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，第 1 秒 有 1/3 的概率跳到顶点 2 ，然后第 2 秒 有 1/2 的概率跳到顶点 4，因此青蛙在 2 秒后位于顶点 4 的概率是 1/3 * 1/2 = 1/6 = 0.16666666666666666 。

示例 2：

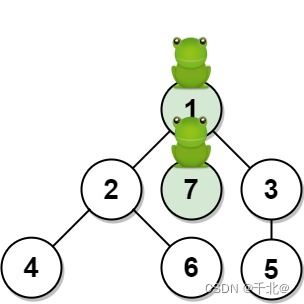
输入：n = 7, edges = [[1,2],[1,3],[1,7],[2,4],[2,6],[3,5]], t = 1, target = 7
输出：0.3333333333333333
解释：上图显示了青蛙的跳跃路径。青蛙从顶点 1 起跳，有 1/3 = 0.3333333333333333 的概率能够 1 秒 后跳到顶点 7 。

提示：

1 <= n <= 100
edges.length == n - 1
edges[i].length == 2
1 <= ai, bi <= n
1 <= t <= 50
1 <= target <= n

方法：深度优先搜索

首先我们根据 edges 求出树的邻接表，方便我们对图进行搜索。并且定义数组 seen 用来记录已经遍历过的顶点。此外 dfs 的参数还包括当前遍历的顶点序号，和剩余时间 t。青蛙从顶点1开始起跳，所以我们从定点 1 开始进行搜索，初始剩余时间为 t。

每次遍历一个节点时候，如果当前节点没有后续节点，或者剩余时间为 0，我们不能继续搜索了。此时当前节点是 target ，我们返回概率 1.0，否则返回概率为 0.0。如果有后续节点，并且剩余时间不为 0，我们继续深度优先搜索，如果有子节点返回概率 p > 0，说明已经找到了节点 target ，又因为跳到任意一个后续子节点上的机率都相同，我们返回概率 p 除以后续节点个数的商，作为最后的结果。

代码：

class Solution {
public:
    double frogPosition(int n, vector<vector<int>>& edges, int t, int target) {
        vector<vector<int>> G(n + 1);
        for (int i = 0; i < edges.size(); ++i) {
            G[edges[i][0]].push_back(edges[i][1]);
            G[edges[i][1]].push_back(edges[i][0]);
        }
        vector<bool> visited(n + 1, false);
        return dfs(G, visited, 1, t, target);
    }

    double dfs(vector<vector<int>>& G, vector<bool>& visited, int i, int t, int target) {
        int nxt = i == 1 ? G[i].size() : G[i].size() - 1;
        if (t == 0 || nxt == 0) {
            return i == target ? 1.0 : 0.0;
        }
        visited[i] = true;
        double ans = 0.0;
        for (int j : G[i]) {
            if (!visited[j]) {
                ans += dfs(G, visited, j, t - 1, target);
            }
        }
        return ans / nxt;
    }
};