引言
- 题型总结中推荐例题有蓝皮书的题型较为重要,只有吉米多维奇的题型次之。
- 码字不易,如果这篇文章对您有帮助的话,希望您能点赞、评论、收藏,投币、转发、关注。您的鼓励就是我前进的动力!
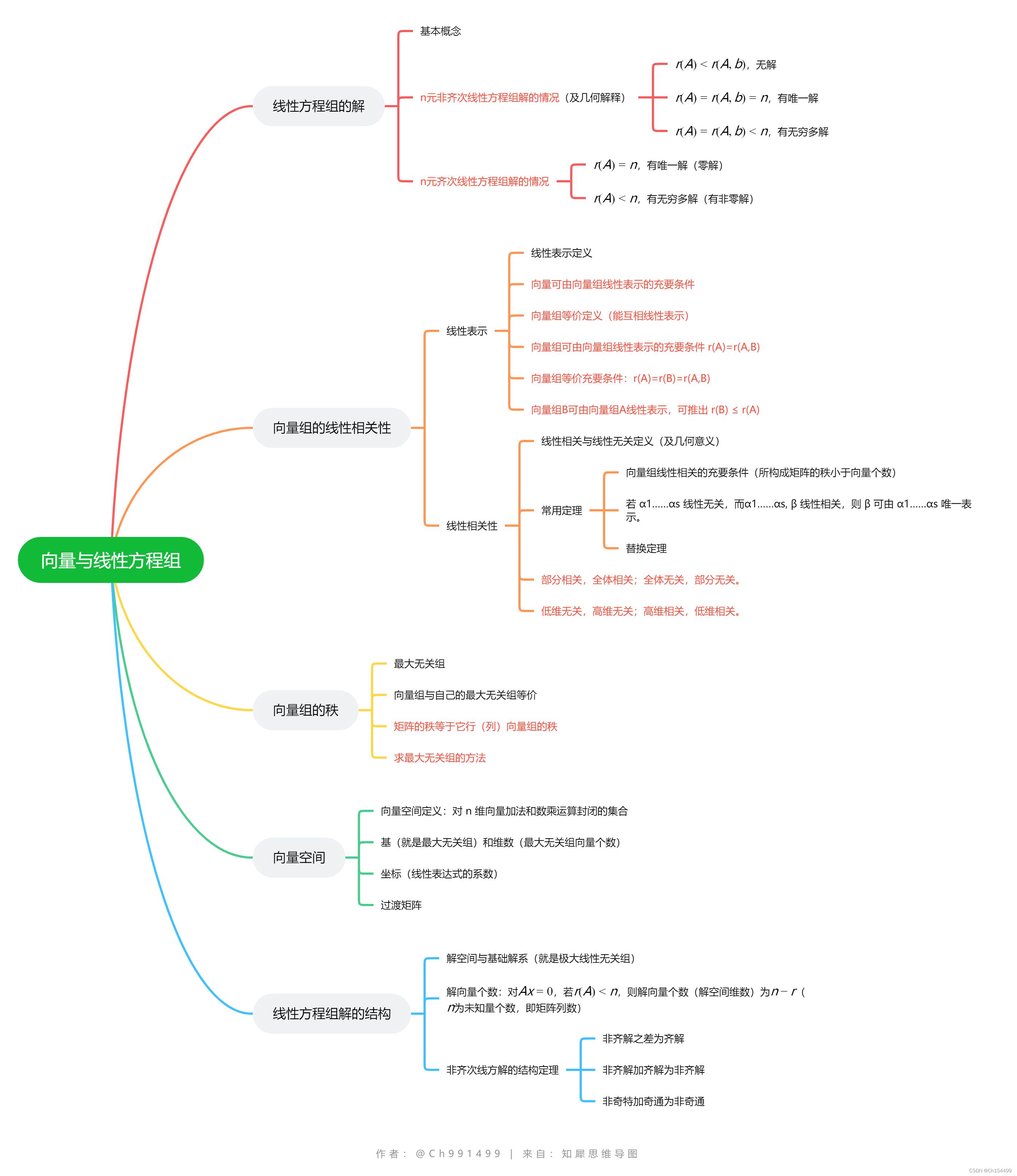
知识点思维导图
补充:
- 零向量可由任意向量表示。
- 向量组中任一向量可由向量组表示。
- 任意向量均可由向量 ( 1 , 0 , … , 0 ) , ( 0 , 1 , … , 0 ) … ( 0 , 0 , … , 1 ) … (1,0,…,0),(0,1,…,0)…(0,0,…,1)… (1,0,…,0),(0,1,…,0)…(0,0,…,1)…表示。
- 向量组中两向量成比例,线性相关。
- 含零向量的向量组必相关。
- 一个零向量必相关;一个非零向量必无关。
- “相关长,无关短”原理:
1) 增长原理(判断相关): 若 a 1 , a 2 … a n a_1,a_2…a_n a1,a2…an 线性相关,则 a 1 , a 2 … a n , a n + 1 , … a s a_1,a_2…a_n,a_{n+1},…a_s a1,a2…an,an+1,…as 也线性相关。
2) 截短原理(判断无关):若 a 1 , a 2 … a n a_1,a_2…a_n a1,a2…an 线性无关,则 a 1 , a 2 … a n − s ( 0 < s < n ) a_1,a_2…a_{n-s} (0<s<n) a1,a2…an−s(0<s<n) 也线性无关。
3)可据此记忆结论:部分相关,全体相关;全体无关,部分无关。 - 等价的线性无关组含向量的个数相同。
- 若 a 1 , a 2 … a s a_1,a_2…a_s a1,a2…as 线性无关,则 r ( A ) = s r(A)=s r(A)=s;若 a 1 , a 2 … a s a_1,a_2…a_s a1,a2…as 线性相关,则 r ( A ) < s r(A)<s r(A)<s。
- 向量空间中,零元素和负元素都是唯一的。
- 求向量在某个基中的坐标,就是求线性表达式的系数。
易错点
NULL
题型总结
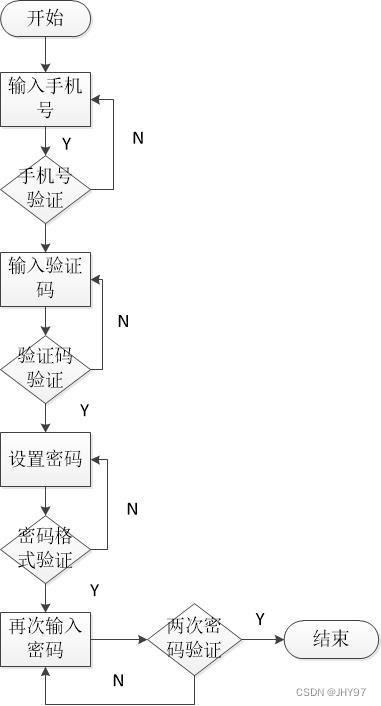
一、求 A x = b Ax=b Ax=b解的情况
- 步骤:
1)写出增广矩阵。
2)用行变换,将矩阵化为阶梯形(不需要化成行最简)。
3)根据 r ( A ) , r ( A , b ) , n r(A), r(A,b), n r(A),r(A,b),n判断解的情况。
4)若为无穷多解,化为行简化阶梯形。不管零行,非零行的首非零元留在左边,其余元素挪到右边,得到一般解。 - 出题都是一般无穷多解的情况。
- 有未知量的行列式求解时,未知量不能放在分母处(可能为零)
- 齐次方程一定有解。
- 为了方便,齐次方程运算使用系数矩阵,不用增广矩阵。
二、判断向量能否由某个向量组线性表示
- 理论依据:一个向量能由某个向量组线性表示的充要条件是:向量组组成的矩阵的秩等于向量组和要线性表示的向量一起组成的矩阵的秩。
- 解题步骤:
1)不用管给的向量是行向量还是列向量,均将向量组中的向量按列作为方程组的系数,要表示的向量作为右端常数项,写出增广阵。
2)化增广阵为行阶梯形,若 r ( A ) = r ( A , b ) r(A)=r(A,b) r(A)=r(A,b)则可以线性表示。 - 判断两个向量组之间能否线性表示或等价(能互相线性表示),可扩展此方法,将要表示的向量换做要表示的向量组即可。
三、求最大无关组并用其表示其余向量
- 步骤:
1)将向量组按列构成矩阵。
2)只用行变换化为行最简阶梯形。
3)首非零元所在的列的向量就是极大无关组。
4)其余向量,其所在列的元素为线性表示的对应系数,直接对应写出即可。
四、求齐次方程的通解
- 步骤:
1)对系数阵用行变换化为行最简形。
2)非零行的首非零元的 1 1 1留在左边,其余元素挪到右边。得同解方程组。
3)令自由未知量取 ( 1 , 0 , … , 0 ) T , ( 0 , 1 , … , 0 ) T … ( 0 , 0 , … , 1 ) T … (1,0,…,0)^T,(0,1,…,0)^T…(0,0,…,1)^T… (1,0,…,0)T,(0,1,…,0)T…(0,0,…,1)T…,代入同解方程组,得基础解析。
4)基础解系乘以对应的实数(如 k 1 , k 2 ∈ R k_1,k_2∈R k1,k2∈R)之和即为通解。
五、求非其次方程通解
- 理论依据:非其次方程的通解等于非齐次方程的特解加对应的齐次方程的通解。
- 步骤:
1)写出增广阵,只用行变换化为最简形。
2)非零行的首非零元的 1 1 1留在左边,其余的挪到右边。写出非齐次的同解方程组,指出谁是自由未知量(不在左边的)。
3)令自由未知量均取零,得 A x = 0 Ax=0 Ax=0的一个特解。
4)令同解方程组右边常数项均为零,得齐次方程的同解方程组,指出谁是自由量。
5)令自由量取相应值,的得 A x = 0 Ax=0 Ax=0的基础解系。
6)非齐次方程的特解加齐次方程的通解,即为非齐次方程的通解。
其余题型
NULL
方法心得
- 根据方程组 A x = b Ax=b Ax=b 的增广矩阵(行阶梯形)判断解的情况或秩的情况技巧:在行阶梯矩阵下方非零数与零之间画分界线,若该线条在解向量与右端向量之间不拐弯(一条直线过去),则有解( r ( A ) = r ( A , b ) r(A)=r(A,b) r(A)=r(A,b));若拐弯了(先竖再横),则无解( r ( A ) < r ( A , b ) r(A)<r(A,b) r(A)<r(A,b))。
参考资料:
[1]安徽理工大学数学系. 线性代数(第三版修订). 天津:天津科学技术出版社, 2019.
[2]安徽理工大学数学系. 线性代数、概率论与数理统计同步辅导习题(第二版). 天津:天津科学技术出版社, 2016.
[3]张天德. 线性代数习题精选精解. 山东:山东科学技术出版社, 2009.
[4]《线性代数》高清教学视频 “惊叹号”系列 宋浩老师
![CodeForces.1786A2.发牌.[中等][flg标识][数学规律][双色牌]](https://img-blog.csdnimg.cn/8137059c129646c0887c16f8199edc50.png)